கெப்ளரின் மூன்றாம் விதியும் வானியல் தொலைவுகளும்

கெப்ளரின் மூன்றாம் விதியும் வானியல் தொலைவுகளும்

கெப்ளர் தனது மூன்று விதிகளையும் தருவிப்பதற்கு டைகோ பிராஹேவின் வானியல் தரவுகளை முழுமையாகப் பயன்படுத்தினார். தனது மூன்றாம் விதியில் சூரியனுக்கும் கோளுக்கும் இடையேயான தொலைவுக்கும், கோளின் சுற்றுக் காலத்திற்கும் உள்ள தொடர்பினை தருவித்தார். வானியல் அறிஞர்கள் வடிவியல் மற்றும் முக்கோணவியலின் உதவியுடன் ஒரு கோளுக்கும் சூரியனுக்கும் இடையே உள்ள தொலைவினை புவிக்கும் சூரியனுக்கும் இடையே உள்ள தொலைவின் (வானியல் அலகு) மடங்காகக் கண்டறிந்தார்கள். இங்கு சூரியனிலிருந்து புதன் மற்றும் வெள்ளியின் தொலைவு கண்டறியப்பட்ட விதத்தை காண்போம். புதன் மற்றும் வெள்ளி கோள்கள் உள் கோள்கள் எனப்படுகின்றன. பூமியிலிருந்து பார்க்கும்போது சூரியனுக்கும் வெள்ளிக் கோளுக்கும் இடையே உள்ள அதிகபட்ச கோணம் 46° ஆகும். அதேபோல புதன் கோளுக்கும் சூரியனுக்கும் இடையே உள்ள அதிகபட்ச கோணம் 22.50 ஆகும்.

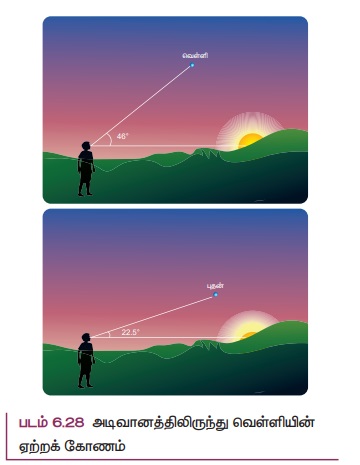
புவியைப் பொறுத்து வெள்ளிக்கோள் பெரும் நீட்சி நிலையில் (460) உள்ளபோது, சூரியனுக்கும், வெள்ளிக்கும் உள்ள கோட்டுக்கும், வெள்ளிக்கும் பூமிக்கும் உள்ள கோட்டுக்கும் இடையே உள்ள கோணம் 90° ஆகும். இதன் மூலம் புவிக்கும் சூரியனுக்கும் இடையே உள்ள தொலைவு காணலாம். புவிக்கும் சூரியனுக்கும் உள்ள தொலைவு ஒரு வானியல் அலகு (1 AU) என்று எடுத்துக் கொள்ளலாம்.

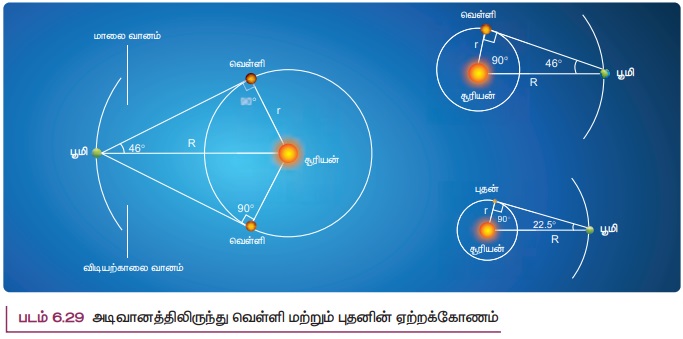
திரிகோணமிதி கொள்கைப்படி படம் 6.29 இல் உள்ள செங்கோண முக்கோணத்தில்

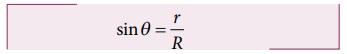
இங்கு R = 1 AU.

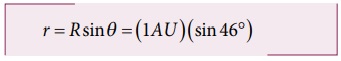
sin 46° = 0.77 என்பதிலிருந்து வெள்ளி சூரியனிலிருந்து 0.77 AU தொலைவில் உள்ளது என கணக்கிடப்பட்டது. இதே போல் θ = 22.50 என பிரதியிட்டு புதனுக்கும் சூரியனுக்கும் உள்ள தொலைவு 0.38 AU என கணக்கிடப்பட்டது. வெளிக்கோள்களான செவ்வாய் மற்றும் வியாழன் போன்ற கோள்களின் தொலைவானது சற்று மாறுபட்ட முறையில் கண்டறியப்பட்டன. அட்டவணை 6.2 இல் சூரியனுக்கும் கோள்களுக்கும் உள்ள தொலைவுகள் தரப்பட்டுள்ளன.

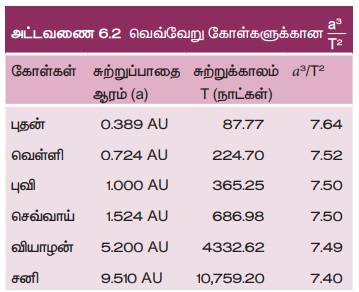
இதிலிருந்து கெப்ளர் விதியைச் சரிபார்க்க உயர்நிலைப் பள்ளியில் கற்கும் வடிவியல் மற்றும் முக்கோணவியல் கருத்துக்களே போதுமானவை என்பது நன்கு தெரிகிறது.