11வது இயற்பியல் : அலகு 6 : ஈர்ப்பியல்

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: பொது ஈர்ப்பியல் விதி

இயற்பியல் : ஈர்ப்பியல் - தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் பொது ஈர்ப்பியல் விதி

எடுத்துக்காட்டு 6.1

படத்தில் காட்டியுள்ளபடி, 10 மீ தொலைவில் நிறைகள் m1 மற்றும் m2 அமைந்துள்ளன. இரு நிறைகளுக்கும் இடையேயான ஈர்ப்பியல் விசையை கணக்கிடுக. ஒவ்வொரு நிறையின் மீது செயல்படும் விசையின் திசையினை வரைக. (m1= 1 kg; m2 = 2 kg)

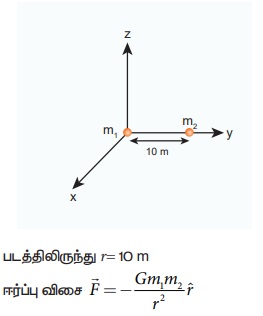
ஃ விசையின் எண் மதிப்பு

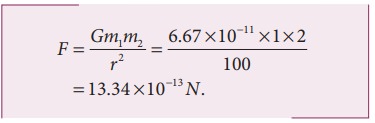
இவ்விசையின் எண் மதிப்பு மிகக்குறைவாக உள்ளது என்பது கவனிக்கத்தக்கது. இதனால் தான் இரு மனிதர்களுக்கிடையேயான ஈர்ப்பியல் விசையை நாம் உணர முடிவது இல்லை. ஈர்ப்பியல் விசையின் வலிமையை நிர்ணயம் செய்வதில் G-ன் மிகக்குறைந்த மதிப்பு முக்கியப் பங்காற்றுகிறது.

நிறை m1 ஆல் நிறை m2 உணரும் ஈர்ப்பியல் விசை () yஅச்சு எதிர்த்திசையில் செயல்படுகிறது. அதாவது rˆ =−jˆ

நியூட்டனின் மூன்றாம் விதிப்படி, நிறை m1 ஆனது நிறை m2 மீது நிறை சமமான எதிர்த்திசையில் செயல்படும் விசையை ஏற்படுத்துகிறது. எனவே நிறை m2 ஆல் m1 உணரும் ஈர்ப்பியல் விசை () ஆனது y அச்சின் நேர்திசையில் செயல்படுகிறது. ie., rˆ = jˆ

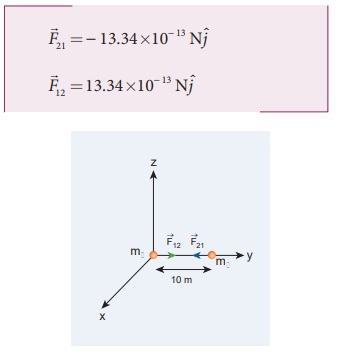
படத்தில் விசைகள் செயல்படும் திசை குறிக்கப்பட்டுள்ளன. மேலும் = − என்பது, நியூட்டனின் மூன்றாம் விதியை உறுதிப்படுத்துகிறது.

எடுத்துக்காட்டு 6.2

நிலவும் ஆப்பிளும் ஒரே ஈர்ப்பியல் விசையாலேயே முடுக்கமடைகிறது. இவை இரண்டும் அடையும் முடுக்கங்களை ஒப்பிடுக.

புவியினால் ஆப்பிள் உணரும் ஈர்ப்பியல் விசை

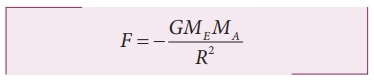
இங்கு MA- ஆப்பிள் நிறை, ME புவியின் நிறை, R - புவியின் ஆரம் ஆகும்.

நியூட்டன் இரண்டாம் விதியைப் பயன்படுத்த

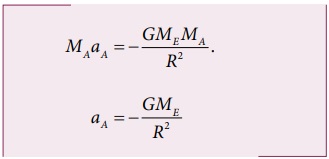
இங்கு ‘aA' ஆப்பிளின் முடுக்கம். இது 'g' க்கு சமம்

இதேபோல் புவியினால் நிலா உணரும் விசை

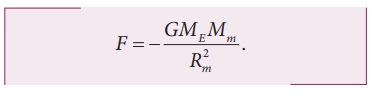
இங்கு Rm - புவிக்கும் நிலாவுக்கும் உள்ள தொலைவு, Mm - நிலாவின் நிறை

நிலா உணரும் முடுக்கம்

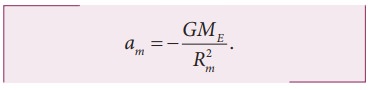
ஆப்பிளின் முடுக்கத்திற்கும், நிலாவின் முடுக்கத்திற்கும் இடையே உள்ள தகவு

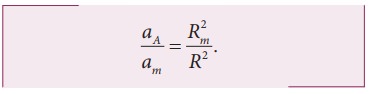
நிலாவின் சுற்றுப்பாதையானது புவியின் ஆரத்தை போல 60 மடங்கு என ஹிப்பார்க்கஸ் (Hipparchus) முன்னரே கண்டறிந்துள்ளார்.

Rm = 60R.

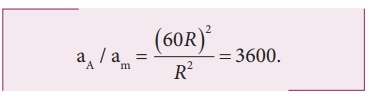
இதன் மூலம் ஆப்பிளின் முடுக்கமானது, நிலாவின் முடுக்கத்தைப் போல 3600 மடங்கு பெரியது என அறிகின்றோம். தனது ஈர்ப்பியல் சமன்பாட்டின் மூலம் இதே முடிவை நியூட்டன் பெற்றார். ஆப்பிளின் முடுக்கம் 9.8ms-2 என எளிதில் கண்டறியப்பட்டது. புவியினை சுற்றும் நிலாவின் சுழற்சிகாலம் 27.3 நாட்கள் என்பதை மைய நோக்கு முடுக்கச் சமன்பாட்டில் பயன்படுத்த, நமக்கு கிடைப்பது

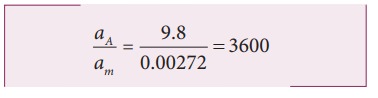
ஈர்ப்பியல் விதியின் மூலமாகவும் இதே மதிப்பினையே நியூட்டன் பெற்றார்.

11th Physics : UNIT 6 : Gravitation : Solved Example Problems for Universal Law of Gravitation in Tamil : 11th Standard TN Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 11வது இயற்பியல் : அலகு 6 : ஈர்ப்பியல் : தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: பொது ஈர்ப்பியல் விதி - : 11 ஆம் வகுப்பு தமிழ்நாடு பள்ளி சமசீர் புத்தகம் கேள்விகள் மற்றும் பதில்கள்.