ஈர்ப்பு நிலை ஆற்றல்

ஈர்ப்பு நிலை ஆற்றல் (Gravitational Potential Energy)

நிலை ஆற்றல் பற்றிய கருத்தும் இயற்பியல் சார்ந்த அதன் பொருள் பற்றியும் முன் பாடங்களில் கற்றுள்ளோம். ஈர்ப்பியல் விசை ஒரு ஆற்றல் மாற்றா விசையாகும். எனவே இந்த ஆற்றல் மாற்றா விசையின் புலத்துடன் தொடர்புடைய ஈர்ப்பு நிலை ஆற்றலை நாம் பின் வருமாறு வரையறை செய்யலாம்.

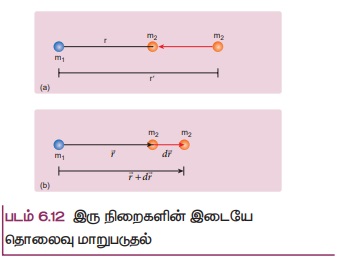
m1 மற்றும் m2 என்ற இரு நிறைகள் ஆரம்பத்தில் r' தொலைவில் உள்ளன. m1 நிறையானது நிலையாக உள்ளது என்க. நிறை m2 ஐ r' நிலையில் இருந்து r நிலைக்கு 6.12 (a) இல் காட்டியுள்ளபடி நகர்த்த வேலை செய்ய வேண்டும்.

நிறை m2 ஐ மிகச் சிறிய தொலைவு d  அதாவது லிருந்து  + d க்கு (படம் 6.12 (b) இல் காட்டியுள்ளபடி) நகர்த்த வெளியிலிருந்து வேலை செய்யப்பட வேண்டும். 

இந்த மிகச்சிறிய வேலை பின் வருமாறு எழுதப்படுகிறது

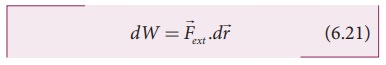
இந்த வேலையானது ஈர்ப்பியல் விசைக்கு எதிராக செய்யப்பட்டுள்ளது. எனவே ஈர்ப்பியல் விசை

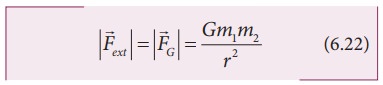
சமன்பாடு 6.22 ஐ 6.21ல் பிரதியிட

r’ ல் இருந்து துகளை r க்கு இடம் பெயரச் செய்த மொத்த வேலை

இந்த வேலை (W) யானது m1, மற்றும் m2, நிறைகள் முறையே r மற்றும் r’ தொலைவில் உள்ள போது அவ்வமைப்பின் ஈர்ப்பு நிலை ஆற்றல்களின் வேறுபாட்டை தருகிறது.

நிலை 1: r > 'r' எனில் 

ஈர்ப்பியல் விசை ஒரு கவர்ச்சி விசை என்பதால் நிறை m2 நிறை m1, ஆல் கவரப்படுகிறது. எனவே நிறை m2, ஐ, r லிருந்து r' க்கு நகர்த்த வெளிப்புறத்திலிருந்து வேலை செய்ய வேண்டிய தேவை இல்லை. இங்கு அமைப்பானது தனது ஆற்றலை செலவழித்து வேலை செய்கிறது. எனவே செய்யப்பட்ட வேலை எதிர்க்குறி பெறும். இது படம் 6.13 (a) இல் காட்டப்பட்டுள்ளது.

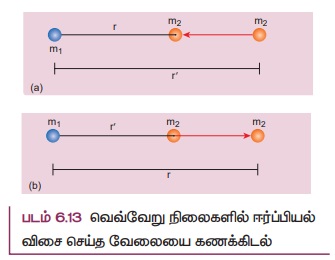
நிகழ்வு 2: r < r' எனில்

r லிருந்து r' க்கு m2 நிறையை நகர்த்த ஈர்ப்பு விசைக்கு எதிராக வேலை செய்ய வேண்டும். எனவே வெளிப்புறத்திலிருந்து வேலையானது செய்யப்பட வேண்டும். ஆகவே செய்யப்பட்ட வேலை நேர்க்குறி மதிப்பைப் பெறுகிறது.

‘’நிலை ஆற்றல் மாறுபாடு’’ என்பதே இயற்பியலில் முக்கியத்துவம் உடையது. தற்போது ஈர்ப்பு நிலை ஆற்றலை நன்கு வரையறுக்க ஒரு ஆதாரப்புள்ளியை தேர்ந்தெடுப்போம் 

அந்த ஆதாரப் புள்ளி r' = ∞ முடிவிலி என்க.

இதன் படி சமன்பாடு (6.28) உள்ள இரண்டாம் பகுதி சுழி ஆகும்.

எனவே

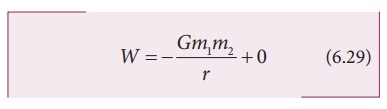
r தொலைவில் அமைந்த நிறைகள் m1 மற்றும் m2 உடைய அமைப்பின் ஈர்ப்பு நிலை ஆற்றலானது, நிறை m1 நிலையாக உள்ளபோது, நிறை m2 வை r தொலைவிலிருந்து முடிவிலாத் தொலைவுக்கு கொண்டு செல்ல செய்த வேலைக்கு சமம் என நாம் வரையறுக்கலாம் ஆகவே ஈர்ப்பு நிலை ஆற்றல்

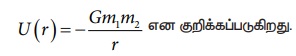
r தொலைவில் அமைந்த நிறைகள் m1 மற்றும் m2 உடைய அமைப்பின் ஈர்ப்பு நிலை ஆற்றலானது, முடிவிலாத் தொலைவு மற்றும் r தொலைவில் இந்த நிறைகளின் அமைப்பு உள்ளபோது பெற்றுள்ள ஈர்ப்பு நிலை ஆற்றல்களின் வேறுபாட்டிற்கு சமம் என்பதும் குறிப்பிடத்தக்கது.

அதாவது U ( r ) = U ( r ) - U ( ∞ ). 

ஆனால் இங்கு U  (∞) = 0 என ஆதாரப்புள்ளியை நாம் தேர்ந்தெடுத்து உள்ளோம்.

ஈர்ப்பு நிலை ஆற்றலானது எப்பொழுதும் எதிர்க் குறி மதிப்பு பெறும். ஏனெனில் முடிவிலாத் தொலைவிலிருந்து நிறைகள் (அமைப்பு) ஒன்றையொன்று மெதுவாக நெருங்கி வரும்போது அமைப்பால் வேலை செய்யப்படுகிறது.

ஈர்ப்பு நிலை ஆற்றல் U ( r ) ன் அலகு ஜுல் (Joule). மேலும் இது ஸ்கேலார் அளவு ஆகும். ஈர்ப்பு நிலை ஆற்றலானது நிறைகளையும் அவற்றுக்கு இடையேயான தொலைவினையும் சார்ந்தது.