வானியல் பற்றிய அடிப்படைக் கருத்துகள்

வானியல் பற்றிய அடிப்படைக் கருத்துகள்

மனிதகுல வரலாற்றில் தோன்றிய மிகப் பழைய அறிவியல் பிரிவு வானியல் ஆகும். முற்காலத்தில் இயற்பியலில் இருந்து பிரித்துப் பார்க்க முடியாத பகுதியாக வானியல் இருந்தது. 16 ஆம் நூற்றாண்டு வரை இயற்பியலில் வானியலின் பங்களிப்பு மிக அதிகம். ஹிப்பார்க்கஸ், அரிஸ்டார்கஸ், தாலமி, கோபர்நிகஸ் மற்றும் டை கோபிராஹே ஆகியோர்களால் பல நூற்றாண்டுகளாக திரட்டப்பட்ட வானியல் தரவுகளின் அடிப்படையில் தான் கெப்ளர் விதிகளும் நியுட்டனின் ஈர்ப்பியல் விதிகளும் உருவாக்கப்பட்டன, உறுதி செய்யப்பட்டன. டைகோ பிராஹே-வின் வானியல் தரவுகள் உதவியின்றி கெப்ளர் விதிகள் உருவாகி இருக்காது. கெப்ளர் விதிகளின் உதவியின்றி நியுட்டன் ஈர்ப்பியல் விதியை உருவாக்கி இருக்க முடியாது. 

பாட ஆரம்பத்தில் கோபர்நிகஸின் சூரிய மையக் கொள்கையானது தாலமியின் புவிமையக் கொள்கைக்கு பதிலாக அமைந்தது எனப்பார்த்தோம். எனவே புவிமையக் கோட்பாட்டின் குறைகளை நாம் பகுத்தாய்ந்து விளக்குவது முக்கியமானதாகும்.

புவிமையக்கொள்கையும் - சூரியமையக் கொள்கையும்

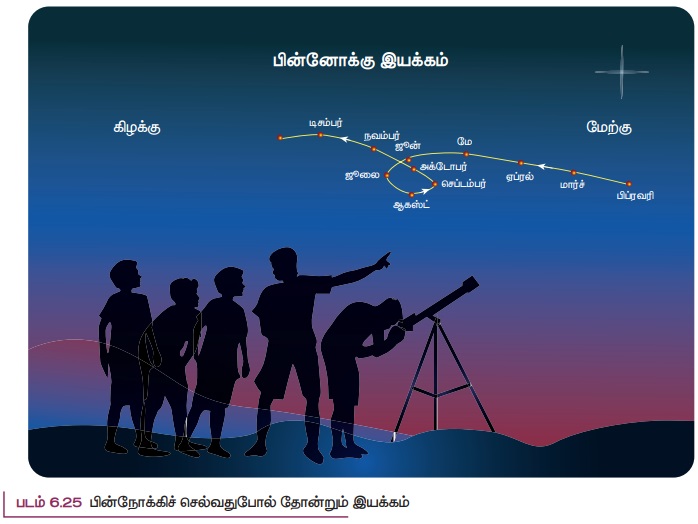
தொடர்ந்து சில மாதங்களுக்கு இரவில் வெறுங்கண்களால் கோள்களின் இயக்கங்களை உற்று நோக்கினோம் எனில் கோள்கள் கிழக்கு திசையில் பயணித்து பின்பு பின்னோக்கி மேற்கு திசையில் இயங்கி மீண்டும் கிழக்கு திசையில் பயணிப்பதை காணலாம். இதற்கு "கோள்களின் பின்னோக்கு இயக்கம்" (Retro grade motion) என்று பெயர். செவ்வாயின் பின்னோக்கு இயக்கத்தை படம் 6.25 இல் காணலாம்.

ஓர் ஆண்டு காலத்திற்கு செவ்வாய் கோளின் இயக்கத்தை உற்று நோக்கும் போது அது முதலில் கிழக்கு திசை நோக்கி (பிப்ரவரி முதல் ஜுன்) செல்லும். பின்பு பின்னோக்கி (ஜுலை, ஆகஸ்டு, செப்டம்பர்) செல்லும். பிறகு அக்டோபர் முதல் மீண்டும் கிழக்கு திசையில் செல்கிறது. முற்காலத்தில் வானியல் அறிஞர்கள் கண்ணுக்கு புலனாகும் அனைத்து கோள்களின் பின்னோக்கு இயக்கத்தை பதிவு செய்து அதனை விளக்க முயற்சி செய்தனர். சூரியன் மற்றும் அனைத்து கோள்களும் புவியை மையமாகக் கொண்டு வட்டப்பாதையில் சுற்றி வருகின்றன என அரிஸ்டாட்டில் கூறினார். அவ்வாறு வட்டப்பாதையில் கோள்கள் இயங்கினால் குறுகிய காலத்திற்கு ஏன் கோள்கள் பின்னோக்கி இயங்குகின்றன? என்பதை விளக்க முடியவில்லை.

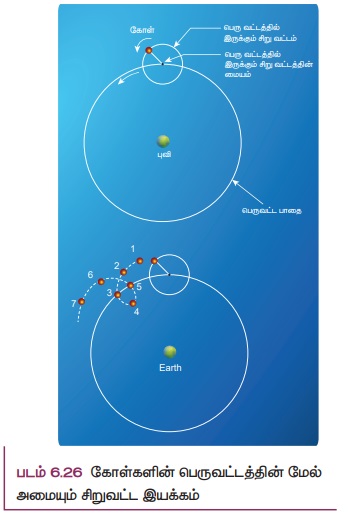
எனவே தாலமி இந்த புவிமையக் கோட்பாடில்" பெருவட்டத்தின் மேல் அமையும் சிறு வட்டச்சுழற்சி (epicycle) என்ற கருத்தினை முன்மொழிந்தார். இக்கருத்தின்படி, புவியினைக் கோள் வட்டப் பாதையில் சுற்றும் அதே வேளையில் மற்றும் ஒரு வட்டப்பாதை இயக்கத்திற்கும் உள்ளாகும். அதற்கு பெருவட்டத்தின் மேல் அமையும் சிறுவட்ட சுழற்சி எனப் பெயர். வட்டப்பாதையில் புவியினை சுற்றும் இயக்கத்தையும், பெருவட்டத்தின் மேல் அமையும் சிறுவட்ட இயக்கத்தையும் ஒன்றிணைக்கும்போது புவியினை ஒரு பொருத்து கோள்கள் பின் நோக்கி செல்வது போல தோன்றும் இயக்கத்தை தருகிறது. அரிஸ்டாட்டிலின் புவிமையக் கருத்துடன் பெருவட்டத்தின் மேல் அமையும் சிறுவட்ட இயக்கத்தை தாலமி இணைத்தார்.

ஆனால் தலாமியின் இந்த சிறு வட்டச் சுழற்சி விளக்கமானது மிகவும் கடினமாக இருந்தது. 15 ஆம் நூற்றாண்டில் போலந்து நாட்டு வானியல் அறிஞர் கோபர்நிக்கஸ், இந்த சிக்கலை எளிய முறையில் தீர்க்கும் விதமாக சூரிய மையக் கொள்கையை முன்மொழிந்தார். இக்கொள்கைப்படி, சூரிய குடும்ப அமைப்பின் மையம் சூரியனே. அனைத்து கோள்களும் சூரியனைச் சுற்றி வருகின்றன. புவியினைச் சார்ந்து கோள்களின் சார்பு இயக்கத்தின் காரணமாக கோள்கள் ‘’பின் நோக்கி செல்வது போன்ற இயக்கத்தை" (Retrograde motion) பெறுகின்றன. சூரிய மையக் கொள்கையின் அடிப்படையில் கோள்களின் இந்த பின் நோக்கி செல்வது போன்ற இயக்கம் படம் 6.27 இல் காட்டப்பட்டுள்ளது.

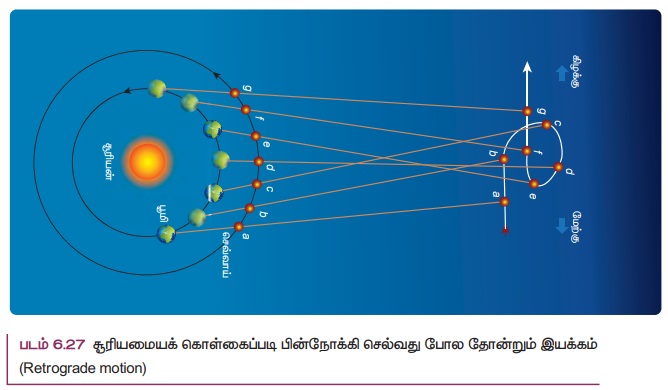
புவியானது செவ்வாய் கோளை விட விரைவாக சூரியனை சுற்றி வருகிறது. புவிக்கும் செவ்வாய் கோளுக்கும் இடையேயான சார்பு இயக்கத்தின் (Relativemotion) காரணமாக ஜுலை முதல் அக்டோபர் வரை செவ்வாய் கோள் பின் நோக்கி செல்வது போல தோன்றுகிறது. இதே போல பிற கோள்களின் பின்னோக்கு இயக்கங்களையும் கோபர் நிகஸின் சூரிய மையக் கொள்கையால் விளக்க முடிந்தது. இந்த எளிமைத் தன்மையின் காரணமாகவே சூரிய மையக் கொள்கை புவி மையக் கொள்கைக்கு பதிலாக படிப்படியாக ஏற்றுக் கொள்ளப்பட்டது. இயற்கை நிகழ்வுகளுக்கு ஒன்றுக்கு மேற்பட்ட விளக்கங்கள் தரப்படும் போது, எளிமையான விளக்கமே அல்லது மாதிரியே பொதுவாக ஏற்றுக்கொள்ளப்படும். மேற்கூறிய கருத்து மட்டுமல்லாது, தாலமியின் கொள்கைக்கு பதிலாக கோபர்நிகஸ் கொள்கை ஏற்றுக் கொள்ளபட்டதற்கான விரிவான விளக்கத்தை வானியல் நூல்களில் காணலாம்.

செயல்பாடு

மாணவர்கள் செவ்வாயின் இயக்கத்தை வெறும் கண்களால் உற்று நோக்கி அதன் பின்நோக்கு இயக்கத்தை கண்டறியலாம். இதனை கண்டறிய 6 முதல் 7 மாத காலம் தேவைப்படும். எனவே ஜுன் மாதம் முதல் ஆரம்பித்து அடுத்த ஆண்டு ஏப்ரல் மாதம் வரை மாணவன் இரவு வானத்தை உற்றுக் கவனிக்க வேண்டும். பெயருக்கு ஏற்ப சிவந்த நிறமுடைய இக்கோள் விண்ணில் நன்கு ஒளிர்ந்து காணப்படும். விண்ணில் செவ்வாய் கோளின் நிலை அறிய "Google" உதவியை நாடலாம்.

கெப்ளரின் மூன்றாம் விதியும் வானியல் தொலைவுகளும்

கெப்ளர் தனது மூன்று விதிகளையும் தருவிப்பதற்கு டைகோ பிராஹேவின் வானியல் தரவுகளை முழுமையாகப் பயன்படுத்தினார். தனது மூன்றாம் விதியில் சூரியனுக்கும் கோளுக்கும் இடையேயான தொலைவுக்கும், கோளின் சுற்றுக் காலத்திற்கும் உள்ள தொடர்பினை தருவித்தார். வானியல் அறிஞர்கள் வடிவியல் மற்றும் முக்கோணவியலின் உதவியுடன் ஒரு கோளுக்கும் சூரியனுக்கும் இடையே உள்ள தொலைவினை புவிக்கும் சூரியனுக்கும் இடையே உள்ள தொலைவின் (வானியல் அலகு) மடங்காகக் கண்டறிந்தார்கள். இங்கு சூரியனிலிருந்து புதன் மற்றும் வெள்ளியின் தொலைவு கண்டறியப்பட்ட விதத்தை காண்போம். புதன் மற்றும் வெள்ளி கோள்கள் உள் கோள்கள் எனப்படுகின்றன. பூமியிலிருந்து பார்க்கும்போது சூரியனுக்கும் வெள்ளிக் கோளுக்கும் இடையே உள்ள அதிகபட்ச கோணம் 46° ஆகும். அதேபோல புதன் கோளுக்கும் சூரியனுக்கும் இடையே உள்ள அதிகபட்ச கோணம் 22.50 ஆகும்.

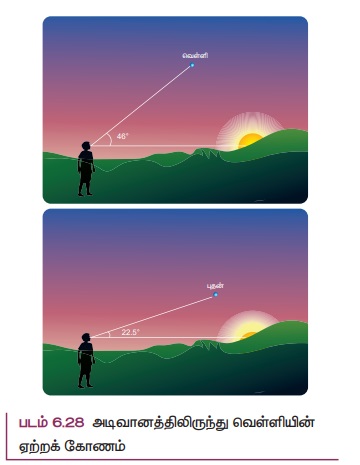
புவியைப் பொறுத்து வெள்ளிக்கோள் பெரும் நீட்சி நிலையில் (460) உள்ளபோது, சூரியனுக்கும், வெள்ளிக்கும் உள்ள கோட்டுக்கும், வெள்ளிக்கும் பூமிக்கும் உள்ள கோட்டுக்கும் இடையே உள்ள கோணம் 90° ஆகும். இதன் மூலம் புவிக்கும் சூரியனுக்கும் இடையே உள்ள தொலைவு காணலாம். புவிக்கும் சூரியனுக்கும் உள்ள தொலைவு ஒரு வானியல் அலகு (1 AU) என்று எடுத்துக் கொள்ளலாம்.

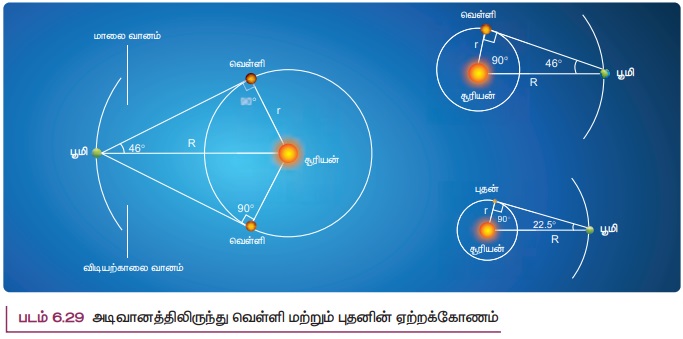
திரிகோணமிதி கொள்கைப்படி படம் 6.29 இல் உள்ள செங்கோண முக்கோணத்தில்

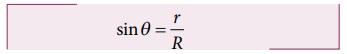
இங்கு R = 1 AU.

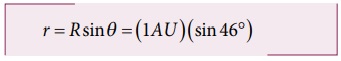
sin 46° = 0.77 என்பதிலிருந்து வெள்ளி சூரியனிலிருந்து 0.77 AU தொலைவில் உள்ளது என கணக்கிடப்பட்டது. இதே போல் θ = 22.50 என பிரதியிட்டு புதனுக்கும் சூரியனுக்கும் உள்ள தொலைவு 0.38 AU என கணக்கிடப்பட்டது. வெளிக்கோள்களான செவ்வாய் மற்றும் வியாழன் போன்ற கோள்களின் தொலைவானது சற்று மாறுபட்ட முறையில் கண்டறியப்பட்டன. அட்டவணை 6.2 இல் சூரியனுக்கும் கோள்களுக்கும் உள்ள தொலைவுகள் தரப்பட்டுள்ளன.

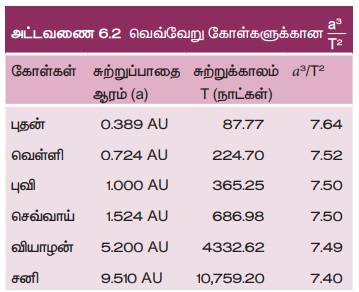
இதிலிருந்து கெப்ளர் விதியைச் சரிபார்க்க உயர்நிலைப் பள்ளியில் கற்கும் வடிவியல் மற்றும் முக்கோணவியல் கருத்துக்களே போதுமானவை என்பது நன்கு தெரிகிறது.

செயல்பாடு

வெள்ளியினை தொலைநோக்கி துணையின்றி வெறும் கண்களால் காண இயலும். சூரிய உதயம் மற்றும் மறைவின் போது வெள்ளியினை நாம் காணலாம். மாணவர்கள் வெள்ளியின் இயக்கத்தினை தொடர்ந்து உற்று நோக்கிட வேண்டும். அதன் மூலம் அதன் பெரும் ஏற்றக்கோணம் 46° என்பதை உறுதி செய்க. மேலும் சூரியனிலிருந்து வெள்ளி உள்ள தொலைவை அளவீடு செய்க. வெள்ளியின் நிலையினை கூகுள் (அல்லது) ஸ்டெல்லாரியம் (Stellarium) செயலி மூலமாக கண்டறியலாம்.

புவியின் ஆரத்தை அளத்தல்:

கி. மு. 225 ல் அலேக்ஸாண்ட்ரியா (Alexandria) வில் வாழ்ந்த கிரேக்க நூலகர் எரட்டோஸ்தனீஸ் ("Eratos thenes") புவியின் ஆரத்தை முதன்முதலில் அளந்தார். தற்போது நவீன முறையில் கண்டறியப்பட்ட மதிப்புடன் ஒப்பிட இம்மதிப்பு கிட்டத்தட்ட துல்லியமாக அமைந்துள்ளது. எரட்டோஸ்தனீஸ் பயன்படுத்திய கணக்கீட்டுக்கு தேவையான கணிதம் இன்று உயர்நிலை வகுப்பில் சொல்லித் தரப்படுகிறது. கோடை சூரிய திருப்பு முக நிலையில் (சூரியன் தன் இயக்க திசையை மாற்றும் நாள்) (Solstice) நண்பகலில் சைன் (Syene) நகரில் சூரிய ஒளி நிழல் ஏற்படுத்தாதைக் கண்டார். அதே நேரத்தில் சையென் நகரிலிருந்து 500 மைல் தொலைவில் உள்ள அலெக்ஸாண்ட்ரியா நகரில் செங்குத்துத் திசைக்கு 7.20 சாய்வாக சூரிய ஒளி நிழல் விழுகிறது எனக் கண்டார் (படம் 6.30)

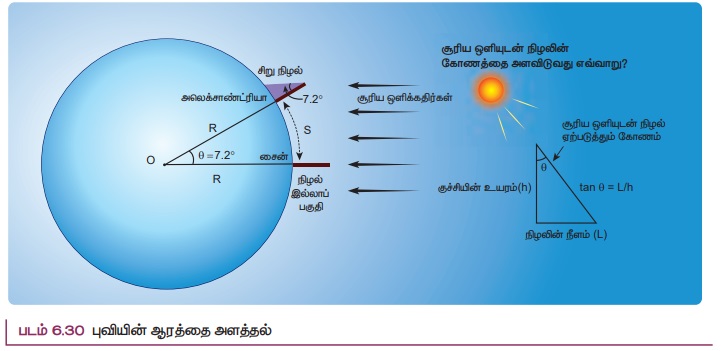
7.2 டிகிரி வேறுபாடு ஏற்படக் காரணம் புவியின் மேற்பரப்பு வளைந்து காணப்படுவதே என உணர்ந்தார். 

இந்த கோணம்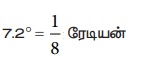

சைன் மற்றும் அலெக்சாண்டிரியா நகருக்கு இடையேயான வட்டவில்லின் நீளம் S என்க.

மேலும் புவியின் ஆரம் R எனில்

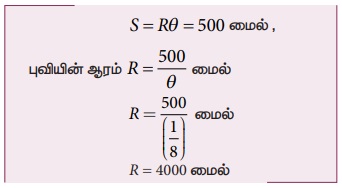
1 மைல் = 1.609 km. எனவே அவர் புவியின் ஆரம் R = 6436 km எனக் கணக்கிட்டார். வியப்பளிக்கும் வண்ணம் இம்மதிப்பு தற்போது கண்டறியப்பட்ட மதிப்பான 6378 km க்கு மிக அருகே உள்ளது.

3 ஆம் நுற்றாண்டில் கிரேக்க நாட்டு வானியல் அறிஞர் ஹிப்பார்க்கஸ் புவிக்கும் நிலவுக்கும் உள்ள தொலைவினை கண்டறிந்தார்.

செயல்பாடு

புவியின் ஆரத்தை அளப்பதற்கு, குறைந்தது 500 km தொலைவில் அமைந்த இரு இடங்களை (பள்ளிகளை) தேர்ந்தெடுக்கவும். இவ்விடங்கள் ஒரே தீர்க்க ரேகையால் (longitude) அமைந்திருக்க வேண்டும். (எடுத்துக்காட்டாக ஓசூரும் கன்னியாகுமரியும் ஒரே குறுக்கு கோட்டில் 77.82° E) அமைந்துள்ளன. h உயரம் உடைய குச்சியை ஒரு மைதானத்தில் செங்குத்தாக நிறுத்தவும். மிகச் சரியாக நண்பகல் வேளையில் இரு இடங்களிலும் கம்பத்தின் நிழலின் நீளத்தை (L) அளவிடவும். படம் 6.30 ல் காட்டியுள்ளபடி படம் வரைக. tan θ = L/h சமன்பாட்டை பயன்படுத்தி ஒவ்வொரு இடத்திலும் கோணத்தின் மதிப்பை (ரேடியனில்) கண்டறிக. இருகோணங்களுக்கும் உள்ள இடையே வேறுபாடு (0') புவிப்பரப்பு வளைந்துள்ளதால் ஏற்படுகிறது. கூகுள் மேப் மூலம் இரு இடங்களுக்கிடையேயான தொலைவினை கண்டறிக. தொலைவினை இக்கோண வேறுபாட்டால் வகுக்க புவியின் ஆரத்தினை கண்டறியலாம்.

வியப்பூட்டும் வானியல் உண்மைகள்

1. சந்திர கிரகணம் மற்றும் புவியின் நிழலின் ஆரம் அளவிடுதலும் 

2018 ஜனவரி 31, அன்று முழு சந்திர கிரகணம் நடைபெற்றதை தமிழகம் உட்பட பல இடங்களில் உற்று நோக்கி பதிவு செய்யப்பட்டது. நிலா புவியின் நிழலைக் கடக்கும்போது, இப்புவி நிழலின் ஆரத்தை அளவீடு செய்யலாம். படம் 6.31ல் இம்முறை விளக்கப்பட்டுள்ளது.

புவியின் கருநிழல் பகுதியில் நிலா உள்ளபோது சிவப்பு நிறத்தில் நிலா தெரியும். புவியின் கருநிழல் பகுதியினை விட்டு நிலா வெளியேறிய உடனே அது பிறைநிலவு போல தோன்றும். அவ்வாறு நிலா வெளியேறும்போது டிஜிட்டல் கேமரா மூலம் எடுக்கப்பட்ட நிழல் படத்தை (படம் 6.32) பார்க்கவும்.

படம் (6.32) இலிருந்து புவி கரு நிழலின் தோற்ற ஆரம் மற்றும் நிலாவின் தோற்ற ஆரம் (படம் 6.33) ஆகியவற்றை அளக்கலாம். பின்பு அவற்றின் தகவு கணக்கிடலாம். (படம் 6.33 மற்றும் படம் 6.34)

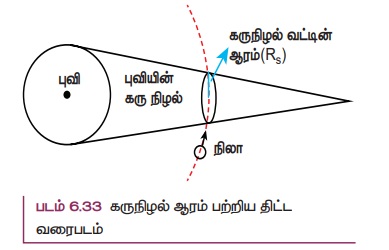
நிழற்படத்தில் புவியின் கருநிழலின் தோற்ற ஆரம் (apparent radius) = Rs = 13.2 cm

நிழற்படத்தில் நிலாவின் தோற்ற ஆரம் (apparent radius) = Rm= 5.15 cm 

இந்த ஆரங்களின் தகவு Rs/Rm ≈ 2.56

புவியின் கருநிழலின் ஆரம் Rs = 2.56 × Rm 

நிலாவின் ஆரம் Rm = 1737 km

புவி கருநிழலின் ஆரம்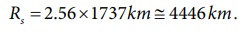

ஆரத்தின் சரியான அளவு = 4610 km.

கணக்கீட்டில் சதவீதப் பிழை

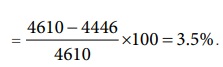
உயர்திறன் தொலை நோக்கி மூலம் படங்கள் எடுக்கப்பட்டால் பிழையின் அளவு குறையும். எளிய கணித செயல்பாட்டின் மூலம் இந்த கணக்கீடு செய்யப்பட்டுள்ளது என்பது கவனிக்கத்தக்கது.

சந்திர கிரகணத்தின் போது நிலாவின் மீது விழும் புவியின் நிழலின் வடிவத்தை உற்றுநோக்கி புவியானது கோளக வடிவமுடையது என வானியல் அறிஞர்கள் வெகு காலத்திற்கு முன்பே நிரூபித்தனர்.

2. ஒவ்வொரு மாதமும் சூரிய கிரகணம் மற்றும் சந்திரகிரகணம் இரண்டுமே தோன்றுவதில்லை ஏன்?

முழு நிலவு நாளின் போது நிலவின் சுற்றுப்பாதையும் புவியின் சுற்றுப்பாதையும் ஒரே தளத்தில் அமைந்தால் சந்திரகிரகணம் தோன்றும். 

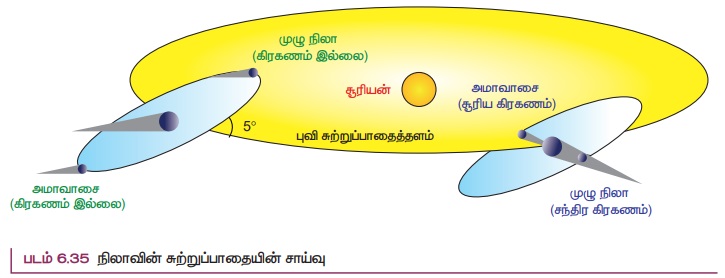
அதேபோல் அமாவாசை அன்றும் அமைந்தால் சூரிய கிரகணம் தோன்றும். ஆனால் நிலாவின் சுற்று பாதையானது புவியின் சுற்றுப்பாதைத் தளத்திலிருந்து 5° சாய்ந்து காணப்படுகிறது. இந்த 5° சாய்வு உள்ளதால், ஆண்டின் ஒரு குறிப்பிட்ட காலத்தில் மட்டுமே சூரியன், புவி மற்றும் நிலவு ஆகியவை ஒரே நேர்கோட்டில் அமைகின்றன. அவ்வாறு அமையும் பொழுது மட்டுமே இம்மூன்றின் நிலையினைப் பொறுத்து சந்திர கிரகணமோ அல்லது சூரிய கிரகணமோ ஏற்படும். இது படம் (6.35)ல் காட்டப்பட்டுள்ளது.

3. புவியில் பருவ காலங்கள் தோன்றுவது ஏன்?

சூரியனை புவி நீள்வட்டப்பாதையில் சுற்றுகிறது. எனவே சூரியனுக்கு அண்மையில் புவி உள்ளபோது கோடைகாலமும் சேய்மையில் உள்ளபோது குளிர்காலமும் தோன்றுகிறது என்பது தவறான கருத்தாகும். உண்மையில் புவியானது சூரியனை 23.5° கோண சாய்வுடன் சுற்றி வருவதாலேயே பருவ காலங்கள் தோன்றுகின்றன’. இது படம் 6.36 ல் காட்டப்பட்டுள்ளது.

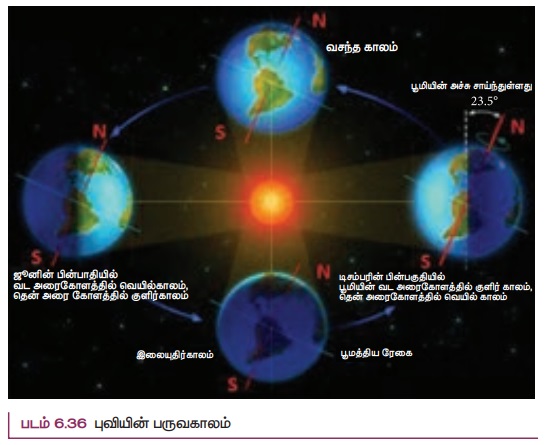
23.5° சாய்வின் காரணமாக புவியின் வடகோளப்பகுதி சூரியனுக்கு வெகுதொலைவில் உள்ள போது, புவியின் தென்கோளப்பகுதி சூரியனுக்கு அருகில் அமையும். எனவே வடகோளப்பகுதியில் குளிர்காலமாக உள்ளபோது, தென்கோளப்பகுதியில் கோடை காலமாக இருக்கும். 

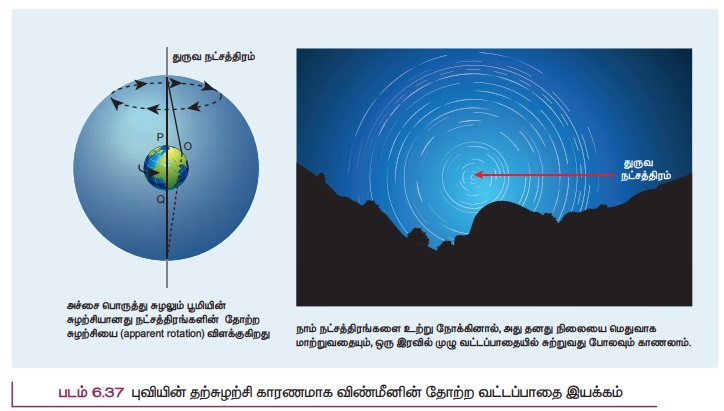
4. விண்மீனின் தோற்ற இயக்கமும் புவியின் சுழற்சியும்

இரவு நேரங்களில் விண்மீன்கள் நகர்வது போது தோன்றுவதை உற்று நோக்குவதன் மூலம் புவி தன்னைத்தானே சுழல்கிறது என நிரூபிக்கலாம். புவியின் தற்சுழற்சி காரணமாகவே துருவ விண்மீனை மற்ற விண்மீன்கள் வட்டப்பாதையில் சுற்றி வருவது போல தோன்றுகிறது (படம் 6.37)

குறிப்பு

புவியின் சுழற்சி அச்சுக்கு நேராக துருவ விண்மீன் அமைந்துள்ளதால் அவ்விண்மீன் நிலையானதாக தோன்றுகிறது. போலாரிஸ் விண்மீனே (Polaris) துருவ விண்மீன் ஆகும்.

சிந்தனைக்கு 

சூரிய ஒளிக்கதிர்களையும் மற்றும் நிழலினையும் பயன்படுத்தி புவியானது 23.5° சாய்ந்துள்ளது என எவ்வாறு நிரூபிப்பாய்?

வானியல் மற்றும் ஈர்ப்பியலில் சமீபத்திய வளர்ச்சிகள்: 

19 ஆம் நூற்றாண்டு வரை வானியலானது வெறும் கண்களால் அல்லது தொலைநோக்கி மூலம் உற்று நோக்கப்படுதலை சார்ந்து இருந்தது. 19 ஆம் நூற்றாண்டின் முடிவில் மின்காந்த அலைகளின் நிறமாலை கண்டறியப்பட்டவுடன் பிரபஞ்சத்தைப் பற்றிய நமது புரிதல் பெருமளவில் அதிகரித்தது. 19 ஆம் நூற்றாண்டின் இறுதியில் ஏற்பட்ட இந்த வளர்ச்சியால் நியூட்டனின் ஈர்ப்பியல் விதியால் சில நிகழ்வுகள் மற்றும் முரண்பாடுகளை விளக்க முடியவில்லை என கண்டறியப்பட்டது. ஈர்ப்பியல் துறையில் 20 ஆம் நூற்றாண்டின் மிகச் சிறந்த கொள்கைகளில் ஒன்றான “பொது சார்பியல் தத்துவம்" ஆல்பர்ட் ஐன்ஸ்டீனால் உருவாக்கப்பட்டது.

இருபதாம் நூற்றாண்டில் வானியலும் ஈர்ப்பியலும் ஒன்றிணைந்தன. மேலும் பல மடங்கு வளர்ச்சி அடைந்தன. விண்மீன் தோற்றமும் மறைவும் எவ்வாறு ஏற்படுகிறது என்பது நன்கு புரிந்து கொள்ளப்பட்டது. வான் இயற்பியல் மற்றும் ஈர்ப்பியல் துறைகளில் இந்திய இயற்பியல் அறிஞர்கள் முக்கிய பங்களிப்புகள் அளித்திருக்கின்றனர். கருந்துளை மற்றும் விண்மீனின் மறைவு பற்றிய கொள்கையினை சுப்பிரமணியன் சந்திரசேகர் உருவாக்கினார். இதற்காக 1983 இல் நோபல் பரிசு பெற்றார். இந்திய வானியல் அறிஞர்களில் குறிப்பிடத்தக்கவரான மேக்நாட் சாகா (Meghanad saha) விண்மீன்களில் நடைபெறும் அயனியாக்கத்திற்கு உரிய சமன்பாட்டை கண்டுபிடித்தார். இது ‘’சாகாவின் அயனியாக்கச் சமன்பாடு’’ எனப்படும். இச்சமன்பாடு விண்மீன்களை வகைப்படுத்த உதவுகிறது. அமல் குமார் சௌத்ரி (Amal Kumar Ray - Choudhuri) உருவாக்கிய ‘’ராய் - சௌத்ரி சமன்பாடும்’’ ஈர்ப்பியல் துறைக்கு மிக சிறந்த பங்களிப்பாகும். இன்னொரு முக்கிய இந்திய வானியற்பியலரான ஜெயந்த் வி.நர்லிகர் (Jayand V.Narlikar) வானியற்பியலில் முன்னோடியான பல பங்களிப்புகளை தந்துள்ளார். மேலும் வானியல் மற்றும் வானியற்பியல் பற்றிய ஆர்வத்தைத் தூண்டும் நூல்கள் பல எழுதியுள்ளார்.

IUCAA (Inter University Center for Astronomy and Astrophysics) என்ற ஆராய்ச்சி நிறுவனம் பேராசிரியர் ஜெயந்த் வி. நர்லிகரால் ஆரம்பிக்கப்பட்டது. இந்நிறுவனம் மூலம் வானியல் மற்றும் ஈர்ப்பியல் துறைகளில் பல்வேறு ஆய்வுகள் நடைபெற்று வருகின்றன.மாணவர்கள் இத்துறைகளில் ஏற்பட்டுள்ள வளர்ச்சிகள் பற்றி நூலகம் சென்று மேலும் அறிந்து கொள்ள வேண்டும்.