12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 3 : சமன்பாட்டியல்
பல்லுறுப்புக் கோவைச் சமன்பாடுகளின் அடிப்படைக் கூறுகள் (Basics of Polynomial Equations)
பல்லுறுப்புக் கோவைச் சமன்பாடுகளின் அடிப்படைக் கூறுகள் (Basics of Polynomial Equations)
1. பல்லுறுப்புக்கோவைச் சமன்பாடுகளின் வகைகள் (Different types of Polynomial Equations)
எந்தவொரு குறையற்ற முழு எண் n −க்கு, x எனும் ஒற்றை மாறியில் n படியுள்ள ஒரு பல்லுறுப்புக் கோவையானது,
P ≡ P(x) = an xn + an−1 xn−1 + ... + a1 x + a0 ஆகும். …………….(1)
இங்கு a, ∈ ℂ ஆகியவை மாறிலிகளாகவும், r = 0, 1, 2, ... , n எனவும், இங்கு an ≠ 0 ஆகும். x எனும் மாறி மெய்யெண் அல்லது கலப்பெண்ணாக இருக்கலாம்.
P எனும் பல்லுறுப்புக் கோவையின் அனைத்து கெழுக்களும் மெய்யெண்கள் எனில், இதனை " ℝ −ன் மீதான பல்லுறுப்புக்கோவை P " என்போம். இதே போன்று, " ℂ −ன் மீதான பல்லுறுப்புக்கோவை P" எனவும், " Q −ன் மீதான பல்லுறுப்புக்கோவை P" எனவும், " ℤ −ன் மீதான பல்லுறுப்புக்கோவை P " எனவும் கலைச்சொற்களைப் பயன்படுத்துகிறோம்.
P எனும் சார்பு, P = P(x) = an xn + an−1 xn−1 + ... + a1 x + a0 என வரையறுக்கப்பட்டு பல்லுறுப்புக் கோவைச் சார்பு என வழங்கப்படுகிறது.
an xn + an−1 xn−1 + ... + a1 x + a0 = 0 …………….(2)
என்பது பல்லுறுப்புக்கோவைச் சமன்பாடு என அழைக்கப்படுகின்றது.
ஏதேனும் சில c ∈ ℂ −க்கு ancn + an−1cn−1 + ... + a1c + a0 = 0 எனில், c என்பது பல்லுறுப்புக்கோவை (1)−ன் ஒரு பூச்சியமாக்கி எனவும், பல்லுறுப்புக் கோவைச் சமன்பாடு (2)−ன் ஒரு மூலம் அல்லது தீர்வு எனவும் அழைக்கப்படுகின்றது.
c என்பது x எனும் ஒரு மாறி உள்ள சமன்பாட்டின் மூலம் எனில், " x = c ஒரு மூலம்" என எழுதுவோம். ar எனும் மாறிலிகள் கெழுக்கள் எனப்படுகின்றது. an எனும் கெழு தலைமைக் கெழு எனவும், anxn என்பது தலைமை உறுப்பு அல்லது முதன்மை உறுப்பு எனவும் அழைக்கப்படுகிறது. கெழுக்கள் மெய்யெண்ணாகவோ அல்லது கலப்பெண்ணாகவோ இருக்கலாம். இதில் விதிக்கப்படும் ஒரே நிபந்தனை என்பது தலைமை கெழு பூச்சியமற்ற எண்ணாக இருக்கவேண்டும். தலைமைக் கெழு 1 என இருக்கும் பல்லுறுப்புக் கோவை தலை ஒற்றை பல்லுறுப்புக் கோவை எனப்படும்.
குறிப்புரை
கீழ்க்காணும் கூற்றுக்களைக் கவனத்தில் கொள்ளவும்
• x −ன் அனைத்து மதிப்புகளுக்கும் பல்லுறுப்புக்கோவைச் சார்புகள் வரையறுக்கப்படுகின்றன.
• ஒவ்வொரு பூச்சியமற்ற மாறிலியும் பூச்சியத்தை படியாகக் கொண்ட பல்லுறுப்புக் கோவையாகும்.
• 0 எனும் மாறிலியும் ஒரு பல்லுறுப்புக்கோவையாகும், இது பூச்சிய பல்லுறுப்புக் கோவை எனப்படுகிறது. இதன் படி வரையறுக்கப்படவில்லை.
• பல்லுறுப்புக்கோவையின் படி ஒரு குறையற்ற முழு எண்ணாக இருக்கும்.
• தலைமை கெழு பூச்சியம் கொண்ட ஒரே பல்லுறுப்புக்கோவை பூச்சிய பல்லுறுப்புக்கோவை மட்டுமே ஆகும்.
• படி இரண்டு உடைய பல்லுறுப்புக்கோவை இருபடிப் பல்லுறுப்புக்கோவை எனப்படும்.
• படி மூன்று உடைய பல்லுறுப்புக்கோவை முப்படிப் பல்லுறுப்புக்கோவை எனப்படும்,
• படி நான்கு உடைய பல்லுறுப்புக்கோவை நாற்படிப் பல்லுறுப்புக்கோவை எனப்படும்,
ஒரு மாறி x−ல் அமைந்த ஒரு பல்லுறுப்புக்கோவையை, x ன் படி இறங்குவரிசையில் அமையுமாறு எழுதுவது வழக்கம். அதாவது மிக உயர்ந்த படி கொண்ட உறுப்பில் தொடங்கி மாறிலி உறுப்பு கடைசி உறுப்பாக இருக்குமாறு எழுதுவது வழக்கம்.
சான்றாக, 2x + 3y + 4z = 5 மற்றும் 6x2 + 7x2y2 + 8z = 9 ஆகியவை x, y, z என்ற மூன்று மாறிகளைக் கொண்ட சமன்பாடுகள் ஆகும்; x2 − 4x + 5 = 0 என்பது x எனும் ஒரு மாறி கொண்ட சமன்பாடு ஆகும். முந்தைய வகுப்புகளில் முக்கோணவியல் சமன்பாடுகள், நேரிய சமன்பாடுகளின் தொகுப்புகள், மற்றும் சில பல்லுறுப்புக் கோவை சமன்பாடுகள் ஆகியவற்றிற்கு தீர்வு கண்டோம்.
x2 −5x + 6 எனும் பல்லுறுப்புக்கோவையின் பூச்சியமாக்கி 3 எனவும் மற்றும் x2 − 5x + 6 = 0 எனும் சமன்பாட்டின் மூலம் அல்லது தீர்வு 3 எனவும் அறிவோம். மேலும் cos(x) = sin(x) மற்றும் cos(x) + sin(x) = 1 ஆகியன x எனும் ஒரு மாறி கொண்ட சமன்பாடுகளாகும். இருப்பினும், cos(x) − sin(x) மற்றும் cos(x) + sin(x) −1 ஆகியன பல்லுறுப்புக் கோவைகளாகாது. எனவே cos (x) = sin (x) மற்றும் cos (x) + sin(x) = 1 ஆகியன "பல்லுறுப்புக் கோவைச் சமன்பாடுகளாகாது".
இப்பாடப்பகுதியில் "பல்லுறுப்புக் கோவைச் சமன்பாடுகளைப் பற்றி மட்டுமே கவனத்தில் கொள்கிறோம். மேலும், ஒரே ஒரு மாறி கொண்ட பல்லுறுப்புக் கோவைச் சமன்பாடு மூலம் தீர்வு காணக்கூடிய சமன்பாடுகளை மட்டுமே கருத்தில் கொள்வோம்.
sin2(x) + cos2(x) = 1 என்பது R −ல் உள்ள முற்றொருமையாகும். அதே சமயத்தில் sin(x) + cos(x) = 1 மற்றும் sin3(x) + cos3(x) = 1 ஆகியன சமன்பாடுகளாகும்.
முக்கியமாக, பல்லுறுப்புக் கோவைகளின் கெழுக்கள் மெய்யெண்களாகவோ அல்லது கலப்பெண்களாகவோ இருந்தாலும் அடுக்குக் குறி குறையற்ற முழுக்களாகத்தான் இருக்க வேண்டும் என்பது குறிப்பிடத்தக்கது. உதாரணமாக, 3x−2 + 1 மற்றும் 5x1/2 + 1 ஆகியன பல்லுறுப்புக்கோவைகளாகாது. பல்லுறுப்புக்கோவைகளைப் பற்றியும், பல்லுறுப்புக் கோவைச் சமன்பாடுகளைப் பற்றியும் குறிப்பாக இருபடிச் சமன்பாடுகளைப் பற்றியும் முன்னரே கற்றுள்ளோம். இப்பாடப்பகுதியில் அவற்றைப் பற்றி சுருக்கமான ஒரு மீள்பார்வையுடன் மேலும் சில கருத்துக்களையும் காண்போம்.
2. இருபடிச் சமன்பாடுகள் (Quadratic Equations)
இருபடிச் சமன்பாடான ax2 + bx + c = 0 −ல், b2 − 4ac என்பது பண்புகாட்டி என அழைக்கப்பட்டு ∆ எனக் குறிப்பிடப்படுகின்றது. ax2 + bx + c எனும் பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்கள் [−b +√∆]/2a மற்றும் [−b −√∆] /2a என்பன ax2 + bx + c = 0 −ன் மூலங்களாகும் என நாமறிவோம். இவ்விரு மூலங்களையும் ஒருங்கே 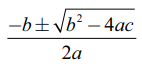 எனக் குறிப்பிடுகிறோம். இங்கு a ≠ 0 எனக் குறிப்பிடுவது தேவையற்றது. ஏனெனில் ax2 + bx + c என்பது இருபடி சமன்பாடு எனக் கூறுவதிலிருந்தே a ≠ 0 என்பது தெளிவாகிறது.
எனக் குறிப்பிடுகிறோம். இங்கு a ≠ 0 எனக் குறிப்பிடுவது தேவையற்றது. ஏனெனில் ax2 + bx + c என்பது இருபடி சமன்பாடு எனக் கூறுவதிலிருந்தே a ≠ 0 என்பது தெளிவாகிறது.
மூலங்கள் சமமாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை ∆ = 0 ஆகும் எனக் கற்றறிந்துள்ளோம். a, b, c என்பன மெய் எனில்
• ∆ > 0 என இருந்தால், இருந்தால் மட்டுமே மூலங்கள் மெய்யாகவும் மற்றும் வெவ்வேறாகவும் இருக்கும்.
• ∆ < 0 என இருந்தால், இருந்தால் மட்டுமே இருபடிச் சமன்பாட்டிற்கு மெய் தீர்வுகள் இருக்காது.