Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ, Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї, Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї, Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї - Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┐Я«»Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«┐Я«ЕЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Vieta's formula for Polynomial Equations) | 12th Maths : UNIT 3 : Theory of Equations
12 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї : Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я««Я»Ї 3 : Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«▓Я»Ї
Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┐Я«»Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«┐Я«ЕЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Vieta's formula for Polynomial Equations)
2. Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┐Я«»Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«┐Я«ЕЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Vieta's formula for Polynomial Equations)
Я«ЄЯ«░Я»ЂЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ«цЯ»ѕ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я»Ї Я«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЅЯ«»Я«░Я»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЋЯ«▒Я»ЇЯ«фЯ»ІЯ««Я»Ї. Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«џЯ«┐Я«▓ Я«цЯ«ЋЯ«хЯ«▓Я»ЇЯ«ЋЯ«│Я»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЅЯ«»Я«░Я»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«цЯ»Ђ Я«јЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«ЋЯ»Ї Я«ЋЯ«▒Я»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї n Я«фЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЋЯ«│Я»ѕЯ«»Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ n Я«фЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»І Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
(a) Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї (The Fundamental Theorem of Algebra)
P(x) = 0 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я««Я»ѓЯ«▓Я««Я»Ї a Я«јЯ«ЕЯ«┐Я«▓Я»Ї (x Рѕњ a) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ P(x) РѕњЯ«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є P(x) РѕњЯ«ЕЯ»Ї Я«фЯ«ЪЯ«┐ РЅЦ 1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ»ѕ P(x) = 0 РѕњЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, (x Рѕњ a)(x Рѕњ b) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ P(x) РѕњЯ«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, P(x) РѕњЯ«ЕЯ»Ї Я«фЯ«ЪЯ«┐ РЅЦ 2 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Є, P(x) = 0 РѕњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ n Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ«ЪЯ«┐ n Я«єЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»І Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, n Я«фЯ«ЪЯ«┐ Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї nРѕњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«цЯ»Ђ.
Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї "Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»Ї" Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЋЯ«▒Я»ЇЯ«▒Я«цЯ»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. P Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ (x Рѕњ a)k Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї (x Рѕњ a)k+l Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, a Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«▓Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»Ї k Я«јЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЅЯ«цЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«Ћ x2 Рѕњ 6x + 9 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x3 Рѕњ 7x2 + 159x РђЊ 9 = 0 Я«єЯ«ЋЯ«┐Я«» Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ 3 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«▓Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»Ї 2 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«▓Я«фЯ»ЇЯ«фЯ»єЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«▓Я»ЂЯ««Я»Ї x2 Рѕњ (4 + 2i)x + 3 + 4i Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x4 Рѕњ 8x3 + 26x2 Рѕњ 40x + 25 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ 2 + i Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«▓Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»Ї 2 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї a Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«▓Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»Ї 1 Я«јЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«▓Я»Ї, a Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«јЯ«│Я«┐Я«» Я««Я»ѓЯ«▓Я««Я»Ї Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
P(x) = 0 РѕњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»ЇЯ«БЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«џЯ»ЄЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»Ђ n Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«Ъ Я«фЯ«ЪЯ«┐ n РѕњЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЁЯ«цЯ»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»ЄЯ«цЯ«ЙЯ«ЕЯ»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я«хЯ»ЄЯ«▒Я»Ђ Я«хЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«џЯ»іЯ«▓Я»ЇЯ«хЯ«цЯ»єЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«▓Я»Ї Рђюn Я«фЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЪЯ«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»ЇЯ«БЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«џЯ»ЄЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ n Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Ї Я«ЄЯ«░Я«ЙЯ«цЯ»Ђ" Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї.
Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«▓Я«┐Я«▓Я»ЄЯ«»Я»Є Я««Я«┐Я«ЋЯ«хЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ЂЯ«хЯ««Я»Ї Я«хЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«ц Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЕЯ»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«еЯ»ѓЯ«▓Я«┐Я«ЕЯ»Ї Я«фЯ«ЙЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»Ђ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я«┐Я«ЕЯ»ЇЯ«▒Я«┐Я«цЯ»Ї Я«цЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 3.1 (Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї) (The Fundamental Theorem of Algebra)
Я«фЯ«ЪЯ«┐ n РЅЦ 1 Я«јЯ«Е Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«еЯ»ЇЯ«цЯ«фЯ«ЪЯ»ЇЯ«џЯ««Я»Ї Я«њЯ«░Я»Ђ Я««Я»ѓЯ«▓Я««Я«ЙЯ«хЯ«цЯ»Ђ Рёѓ РѕњЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«цЯ»ЇЯ«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»Ђ Я««Я»ѓЯ«▓Я««Я«ЙЯ«Ћ n Я«фЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»ЇЯ«БЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«еЯ»ЇЯ«цЯ«фЯ«ЪЯ»ЇЯ«џЯ««Я»Ї n Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Рёѓ РѕњЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї. Я«еЯ««Я«цЯ»Ђ Я«хЯ«┐Я«хЯ«ЙЯ«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї
n Я«фЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Рёѓ РѕњЯ«▓Я»Ї Я«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ n Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»ЇЯ«БЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
Я«џЯ«┐Я«▓ Я«еЯ»ѓЯ«▓Я«ЙЯ«џЯ«┐Я«░Я«┐Я«»Я«░Я»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»ѕЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«ц Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«хЯ«░Я»Ї.
(b) Я«хЯ«┐Я«»Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«┐Я«ЕЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї (Vieta's Formula)
(i) Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┐Я«»Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«┐Я«ЕЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї (Vieta's Formula for Polynomial equation of degree 3)
Я«ЄЯ«ЕЯ«┐ Я«ЄЯ«цЯ»Ђ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЅЯ«»Я«░Я»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
ax3 + bx2 + cx + d = 0.
Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«БЯ»ЇЯ«ЪЯ»Ђ. Я«ЁЯ«хЯ»ѕ ╬▒, ╬▓ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬│ Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є,
ax3 + bx2 + cx + d = a(x Рѕњ ╬▒)(x Рѕњ ╬▓)(x Рѕњ ╬│)
Я«хЯ«▓Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
ax3 + bx2 + cx + d = ax3 Рѕњ a(╬▒ + ╬▓ + ╬│)x2 + a(╬▒╬▓ + ╬▓╬│ + ╬│╬▒)xРѕњ a(╬▒ ╬▓ ╬│).
Я«њЯ«цЯ»ЇЯ«ц Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ Я«њЯ«фЯ»ЇЯ«фЯ«┐Я«Ъ,
╬▒ + ╬▓ + ╬│ = Рѕњb/a , ╬▒╬▓ + ╬▓╬│ + ╬│╬▒ = c/a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬▒╬▓╬│ = Рѕњd/a Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ«ЪЯ«┐ 3 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, a РЅа 0 Я«јЯ«ЕЯ»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї a РѕњЯ«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ««Я»ЂЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є ╬▒, ╬▓ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬│ Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
x2 РѕњЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ = Рѕњ (╬▒ + ╬▓ + ╬│),
x2 РѕњЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ = ╬▒╬▓ + ╬▓╬│ + ╬│╬▒, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ = Рѕњ╬▒╬▓╬│ .
(ii) Я«фЯ«ЪЯ«┐ n > 3 Я«ЅЯ«ЪЯ»ѕЯ«» Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┐Я«»Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«┐Я«ЕЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї (Vieta's Formula for Polynomial equation of degree n > 3)
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї n Я«ЅЯ«»Я«░Я»ЇЯ«фЯ«ЪЯ«┐ Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»єЯ«»Я»ЇЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«њЯ«░Я»Ђ n Я«фЯ«ЪЯ«┐ Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ«▓Я»ѕЯ«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї a1, a2, ... , an Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
xnРѕњ1РѕњЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ = РѕЉ1 = РѕњРѕЉ ╬▒1
xnРѕњ2РѕњЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ = РѕЉ2 = РѕЉ ╬▒1 ╬▒2
xnРѕњ3РѕњЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ = РѕЉ3 = РѕњРѕЉ ╬▒1 ╬▒2 ╬▒3
x РѕњЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ = РѕЉnРѕњ1 = (Рѕњ1)nРѕњ1РѕЉ ╬▒1 ╬▒2 Рђд ╬▒nРѕњ1
x0 РѕњЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ = Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ = РѕЉn = (Рѕњ1)n ╬▒1 ╬▒2 Рђд ╬▒n

Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ РѕЉ╬▒1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї, РѕЉ╬▒1╬▒2 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«┐Я«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я«фЯ«▓Я«ЕЯ»Ї, РѕЉ ╬▒1╬▒2╬▒3 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я««Я»ЂЯ««Я»ЇЯ««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Ћ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я«фЯ«▓Я«ЕЯ»Ї, Я«јЯ«ЕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«хЯ»ЇЯ«хЯ«БЯ»ЇЯ«БЯ««Я»Є Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ»іЯ«▓Я»ЇЯ«▓Я«┐Я«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Є Я«фЯ»ІЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, ╬▒ , ╬▓ , ╬│ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬┤ Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«еЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЪЯ«┐ (Я«џЯ«цЯ»ЂЯ«░Я»Ї) Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, РѕЉ ╬▒1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ РѕЉ ╬▒ Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї, РѕЉ ╬▒1╬▒2 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ РѕЉ ╬▒╬▓ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї
Я«єЯ«ЋЯ«хЯ»Є,
РѕЉ ╬▒ = ╬▒ + ╬▓ + ╬│ + ╬┤
РѕЉ╬▒╬▓ = ╬▒╬▓ + ╬▒╬│ + ╬▒╬┤ + ╬▓╬│ + ╬▓╬┤ + ╬│╬┤
РѕЉ╬▒╬▓╬│ = ╬▒╬▓╬│ + ╬▒╬▓╬┤ + ╬▒╬│╬┤ + ╬▓╬│╬┤
РѕЉ╬▒╬▓╬│╬┤ = ╬▒╬▓╬│╬┤
Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«│Я«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«ЙЯ«Е Я«јЯ«БЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«цЯ»ЇЯ«цЯ«ЋЯ»ѕЯ«» Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«хЯ«џЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я«ЁЯ«цЯ«┐Я«Ћ Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«БЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѕЯ«»Я«ЙЯ«│Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«хЯ«ЕЯ««Я»Ї Я«цЯ»ЄЯ«хЯ»ѕ. Я«ЅЯ«цЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«Ћ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї 1, 2, 2, Я«јЯ«ЕЯ«┐Я«▓Я»Ї, РѕЉ╬▒ = 5 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕЉ╬▒╬▓ = (1├Ќ2) + (1 ├Ќ 2) + (2 ├Ќ 2) = 8.
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«хЯ«┐Я«хЯ«ЙЯ«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, Я«њЯ«░Я»Ђ Я«цЯ«▓Я»ѕЯ«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▒Я»ЇЯ«фЯ«▓Я«ЕЯ»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ xnРѕњ1 РѕњЯ«ЕЯ»Ї Я«ЋЯ»ЂЯ«БЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕ (Рѕњ1)РѕњЯ«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▒Я»ЇЯ«фЯ«▓Я«ЕЯ»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ѕ (Рѕњ1)n РѕњЯ«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 3.3
╬▒, ╬▓, ╬│ Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ»ѕ x3 + px2 + qx + r = 0 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї РѕЉ [ 1/╬▓╬│ ] РѕњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
x3 + px2 + qx + r = 0 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї a, ╬▓, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 7 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї,
РѕЉ1 ╬▒ + ╬▓ + ╬│ = Рѕњp Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕЉ3 ╬▒╬▓╬│ = Рѕњr
Я«јЯ«ЕЯ«хЯ»Є,
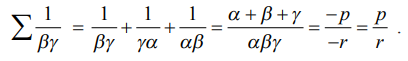
(c) Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«хЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї (Formation of Polynomial Equations with given Roots)
Я«ЄЯ«░Я»ЂЯ«фЯ«ЪЯ«┐Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЁЯ««Я»ѕЯ«цЯ»ЇЯ«цЯ»ІЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ, Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЅЯ«»Я«░Я»ЇЯ«фЯ«ЪЯ«┐ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«јЯ«ЎЯ»ЇЯ«ЎЯ«ЕЯ««Я»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЋЯ«▒Я»ЇЯ«фЯ»ІЯ««Я»Ї. a1,a2, Рђд. , an Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«ЪЯ»ѕЯ«» Я«њЯ«░Я»Ђ n Я«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«цЯ»Ђ? Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▒Я»ЇЯ«фЯ«▓Я«ЕЯ«ЙЯ«Ћ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«хЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«┤Я«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, ╬▒1, ╬▒2, Рђд ╬▒n Я«јЯ«Е Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«» Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
(x Рѕњ ╬▒1)(x РђЊ ╬▒2)(x РђЊ ╬▒3) ... (x РђЊ ╬▒n) = 0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«хЯ«цЯ»Ђ Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я«▓Я»ЇЯ«▓. Я«цЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«┤Я»ЂЯ«ц Я«ЁЯ«цЯ«┐Я«Ћ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«цЯ»ЄЯ«хЯ»ѕ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«еЯ»ЄЯ«░Я«ЪЯ«┐Я«»Я«ЙЯ«Ћ Я«еЯ««Я»ЇЯ««Я«ЙЯ«▓Я»Ї Я«јЯ«│Я«┐Я«цЯ«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«цЯ«┐Я«хЯ«┐Я«Ъ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ«хЯ«цЯ»ЂЯ««Я«ЙЯ«Ћ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ««Я«▓Я»ЄЯ«»Я»Є Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«│Я»ЇЯ«│ x РѕњЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«┐Я«хЯ«┐Я«Ъ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї.
Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї ╬▒, ╬▓, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬│ Я«ЅЯ«ЪЯ»ѕЯ«» Я«њЯ«░Я»Ђ Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
x3 Рѕњ (╬▒ + ╬▓ + ╬│)x2 + (╬▒╬▓ + ╬▓╬│ + ╬│╬▒)x Рѕњ ╬▒╬▓╬│ = 0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
╬▒1, ╬▒2, Рђд ╬▒n Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ n Я«фЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ
xn РђЊ (РѕЉ ╬▒1)xnРѕњ1 + (РѕЉ ╬▒1 ╬▒2 )xnРѕњ2 Рѕњ (РѕЉ ╬▒1 ╬▒2 ╬▒3)xnРѕњ3 +... + (Рѕњ1)n ╬▒1╬▒2 Рђд ╬▒n = 0 Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, РѕЉ╬▒1, РѕЉ╬▒1 ╬▒2 , РѕЉ ╬▒1╬▒2╬▒3 ,... Я«єЯ«ЋЯ«┐Я«»Я«Е Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«░Я»Є Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«хЯ»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЅЯ«цЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«Ћ, 1, Рѕњ2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 3 Я«єЯ«ЋЯ«┐Я«» Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
x3 Рѕњ (1Рѕњ 2 + 3)x2 + (1 ├Ќ (Рѕњ2) + (Рѕњ2) ├Ќ 3 + 3 ├Ќ 1)x РђЊ 1 ├Ќ (Рѕњ2) ├Ќ 3 = 0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«цЯ«ЕЯ»ѕЯ«џЯ»Ї Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ x3 + 2x2 Рѕњ 5x + 6 = 0 Я«јЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. (x Рѕњ1)(x + 2)(x Рѕњ 3) = 0 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ««Я»Є x3 + 2x2 Рѕњ 5x + 6 = 0 Я«јЯ«Е Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ Я«єЯ«░Я»ЇЯ«хЯ««Я«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ«┐Я«»Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 3.4
ax4 + bx3 + cx2 + dx + e = 0 РѕњЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ a РЅа 0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
ax4 + bx3 + cx2 + dx + e = 0 РѕњЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї ╬▒, ╬▓, ╬│ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬┤ Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є,
РѕЉ1 = ╬▒ + ╬▓ + ╬│ + ╬┤ = Рѕњ b/a ,
РѕЉ2 = ╬▒ ╬▓ + ╬▒ ╬│ + ╬▒ ╬┤ + ╬▓ ╬│ + ╬▓ ╬┤ + ╬│ ╬┤ = c/a ,
РѕЉ3 = ╬▒ ╬▓ ╬│ + ╬▒ ╬▓ ╬┤ + ╬▒ ╬│ ╬┤ + ╬▓ ╬│ ╬┤ = Рѕњ d/a ,
РѕЉ4 = ╬▒╬▓╬│╬┤ = e/a .
╬▒2 + ╬▓2 + ╬│2 + ╬┤2 РѕњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»єЯ«ЕЯ«┐Я«▓Я»Ї,
(a + b + c + d)2 РЅА a2 + b2 + c2 + d2 + 2(ab + ac + ad + bc+ bd + cd)
Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ««Я»ѕЯ«»Я«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є,
╬▒2 + ╬▓2 + ╬│2 + ╬┤2 = (╬▒ + ╬▓ + ╬│ + ╬┤)2 Рѕњ 2(╬▒ ╬▓ + ╬▒ ╬│ + ╬▒ ╬┤ + ╬▓ ╬│ + ╬▓ ╬┤ + ╬│ ╬┤)
= (Рѕњ b/a)2 Рѕњ2(c/a)
= (b2 Рѕњ2ac)/ a2
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 3.5
x3 + ax2 + bx + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї p : q : r Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«» Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї p : q : r Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ, p╬╗, q╬╗ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї r╬╗ Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ. Я«ЄЯ«ЕЯ«┐,
РѕЉ1 = p╬╗ + q╬╗ + r╬╗ = Рѕњa, Рђд.. (1)
РѕЉ2 = = (p╬╗)(q╬╗) + (q╬╗)(r╬╗) + (r╬╗)(p╬╗) = b, ........(2)
РѕЉ3 = (p╬╗)(q╬╗)(r╬╗) = Рѕњc, Рђд....(3)
(1) РЄњ ╬╗ = Рѕњ a/ (p + q + r) Рђд....(4)
(3) РЄњ ╬╗3 = Рѕњ c/pqr ...........(5)
(4) РѕњЯ«љ (5)РѕњЯ«▓Я»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ, Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ
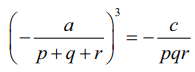 РЄњ pqra3 = c(p + q + r)3
РЄњ pqra3 = c(p + q + r)3
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 3.6
x3 + ax2 + bx + c = 0 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
x3 + ax2 + bx + c = 0 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї ╬▒, ╬▓, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬│ Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є,
РѕЉ1 = ╬▒ + ╬▓ + ╬│ = Рѕњ a , Рђд.. (1)
РѕЉ2 = ╬▒ ╬▓ + ╬▓ ╬│ + ╬│ ╬▒ = b , Рђд.. (2)
РѕЉ3 = ╬▒╬▓╬│ = Рѕњc. Рђд.. (3)
╬▒2, ╬▓2, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬│2 Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕ Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
(1), (2) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (3) Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐, Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ«хЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«хЯ»ІЯ««Я»Ї :
РѕЉ1 = ╬▒2 + ╬▓2 + ╬│2 = (╬▒ + ╬▓ + ╬│)2 Рѕњ 2(╬▒ ╬▓ + ╬▓ ╬│ + ╬│ ╬▒) = (Рѕњa2) РђЊ 2(b) = a2 Рѕњ 2b ,
РѕЉ2 = ╬▒2 ╬▓2 + ╬▓2 ╬│2 + ╬│2 ╬▒2 = (╬▒ ╬▓ + ╬▓ ╬│ + ╬│ ╬▒)2 Рѕњ 2((╬▒ ╬▓)(╬▓ ╬│) + (╬▓ ╬│)(╬│ ╬▒) + (╬│ ╬▒) (╬▒ ╬▓))
= (╬▒ ╬▓ + ╬▓ ╬│ + ╬│ ╬▒)2 Рѕњ2 ╬▒╬▓╬│ (╬▓ + ╬│ + ╬▒) = (b)2 = Рѕњ2(Рѕњc)(Рѕњa) = b2 Рѕњ 2ca
РѕЉ3 = ╬▒2 ╬▓2 ╬│2 = (╬▒ ╬▓ ╬│)2 = (Рѕњc)2 = c2
Я«јЯ«ЕЯ«хЯ»Є, Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ,
x3 Рѕњ (╬▒2 + ╬▓2 + ╬│2)x2 + (╬▒2 ╬▓2 + ╬▓2 ╬│2 + ╬│2 ╬▒2)x Рѕњ ╬▒2 ╬▓2 ╬│2 = 0.
x3 Рѕњ (a2 Рѕњ2b)x2 + (b2 Рѕњ 2ca)x Рѕњ c2 = 0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 3.7
p Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 4x2 + 4px + p + 2 = 0 Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ѕ p РѕњЯ«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«єЯ«░Я«ЙЯ«»Я»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐ Рѕє = (4p)2 Рѕњ 4(4)(p + 2) = 16(p2 РђЊ p Рѕњ 2) = 16(p + 1)(p Рѕњ 2) Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є,
Рѕњ1 < p < 2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Рѕє < 0
p = Рѕњ1 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ p = 2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Рѕє = 0
РђЊРѕъ < p < Рѕњ1 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ 2 < p < Рѕъ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Рѕє > 0
Я«јЯ«ЕЯ«хЯ»Є, Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ,
Рѕњ1 < p < 2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ«▓Я«фЯ»ЇЯ«фЯ»єЯ«БЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї;
p = Рѕњ1 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ p = 2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«џЯ««Я««Я«ЙЯ«Е Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї ;
РѕњРѕъ < p < Рѕњ1 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ 2 < p < Рѕъ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я«ЙЯ«Е Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.