கூடுதல் விவரங்களுடன் கூடிய பல்லுறுப்புக் கோவைகள் (Polynomials with Additional Information)

கூடுதல் விவரங்களுடன் கூடிய பல்லுறுப்புக் கோவைகள் (Polynomials with Additional Information)

இனி உயர்படி பல்லுறுப்புக்கோவைகளுக்குத் தீர்வு காணத் தேவைப்படும் சில கூடுதல் விவரங்களைப் பற்றி ஆராய்வோம். சில சமயங்களில் கூடுதல் தகவல்கள் நேரடியாக அதாவது கொடுக்கப்பட்ட ஒரு மூலம் 2 + 3i எனத் தரப்பட்டிருக்கும். சில சமயங்களில் மறைமுகமாக அதாவது கெழுக்களின் கூட்டல் தொகை பூச்சியம் எனத் தரப்பட்டு பல்லுறுப்புக்கோவையினை ஆய்ந்து கண்டறியும் வகையில் இருக்கும்.

1. கற்பனை மூலங்கள் அல்லது முருடு மூலங்கள் (Imaginary or Surds Roots)

மெய்யெண் கெழுக்களுடைய ஒரு நாற்படி பல்லுறுப்புக்கோவை சமன்பாட்டின் ஒரு மூலம் α +iB என்ற ஒரு மெய்யற்ற கலப்பெண் எனில் α − iβ −ம் ஒரு மூலமாகும்; எனவே, (x − (α + iβ)) மற்றும் (x – (α − iβ)) ஆகியவை பல்லுறுப்புக்கோவை சமன்பாட்டின் காரணிகளாகும். எனவே அதன் பெருக்குத்தொகையும் காரணியாகும். அதாவது, x2 − 2ax + α2 + β2 என்பதும் காரணியாகும். எனவே கொடுக்கப்பட்ட பல்லுறுப்புக்கோவை சமன்பாட்டை இக்காரணியால் வகுக்க, இருபடி பல்லுறுப்புக்கோவையாக ஈவு பெறப்படும். அதனை தெரிந்த வழிமுறைகளைப் பயன்படுத்தி தீர்ப்பதன் மூலம் பல்லுறுப்புக்கோவை சமன்பாட்டின் அனைத்து மூலங்களையும் கண்டறிய இயலும்.

விகிதமுறு கெழுக்களைக் கொண்ட ஒரு இருபடிச் சமன்பாட்டின் ஒரு மூலம் 2 + √3 எனில், 2 − √3 மற்றொரு மூலமாகும்; எனவே (x − (2 + √3))(x − (2 − √3)) −ம் ஒரு காரணியாகும்; x2 − 4x + 1 −ம் ஒரு காரணியாகும். இக்காரணியால் பல்லுறுப்புக்கோவையை வகுத்து ஈவாக பெறப்படும் இருபடி பல்லுறுப்புக்கோவையைத் தெரிந்த வழிமுறைகளைப் பயன்படுத்தித் தீர்க்க இயலும். 2 + √3 இடத்தில் இடம் பெறும் அனைத்து முருடுகளுக்கும் இதே வழிமுறைப் பொருந்தும். இதனைப் பயன்படுத்தி நாற்படி பல்லுறுப்புக்கோவை சமன்பாட்டின் அனைத்து மூலங்களையும் நம்மால் கண்டறிய இயலும்.

விகிதமுறு எண் கெழுக்களுடைய ஓர் அறுபடி பல்லுறுப்புக்கோவையின் ஒரு மூலம் மெய்யற்ற கலப்பெண் மற்றும் ஒரு மூலம் முருடு என அறிந்தால், படிப்படியாக ஆறுபடி பல்லுறுப்புக்கோவைச் சமன்பாட்டின் தீர்வு ஒரு இருபடி சமன்பாட்டின் தீர்வு கணக்காக மாற்றப்பட்டு விடும்.

எடுத்துக்காட்டு 3.15

2 + i மற்றும் 3 − √2 ஆகியவை x6 −13x5 + 62x4  − 126x3 + 65x2 + 127x – 140 = 0 எனும் சமன்பாட்டின் மூலங்கள் எனில் அனைத்து மூலங்களையும் காண்க.

தீர்வு

சமன்பாட்டின் கெழுக்கள் அனைத்தும் விகிதமுறு எண்கள் என்பதாலும் 2 + i மற்றும் 3 − √2 ஆகியவை மூலங்கள் என்பதாலும் கொடுக்கப்பட்ட பல்லுறுப்புக்கோவைச் சமன்பாட்டிற்கு 2 – i மற்றும் 3 + √2 ஆகியவையும் மூலங்களாக அமையும். எனவே, (x − (2 + i)), (x − (2 − i)), (x − (3 − √2)) மற்றும் (x −(3 + √2)) ஆகியவையும் காரணிகளாகும். ஆகையால் இவற்றின் பெருக்கல்

((x − (2 + i)) (x − (2 − i)) (x − (3 − √2)) (x − (3 + √2))

என்பதும் கொடுக்கப்பட்ட பல்லுறுப்புக்கோவை சமன்பாட்டிற்கு ஒரு காரணியாகும். அதாவது, 

(x2 − 4x + 5)(x2 − 6x + 7)

என்பது ஒரு காரணி. கொடுக்கப்பட்ட பல்லுறுப்புக்கோவைச் சமன்பாட்டை இக்காரணியால் வகுக்க, மற்றொரு காரணியாக (x2 − 3x − 4) பெறப்படுகிறது. இதிலிருந்து 4 மற்றும் −1ஆகியவை மற்ற இரு மூலங்களாகும். எனவே,

2 + i, 2 − i, 3 + √2, 3 − √2, −1, மற்றும் 4

ஆகியவை கொடுக்கப்பட்ட பல்லுறுப்புக்கோவைச் சமன்பாட்டின் மூலங்களாகும்.

2. இரட்டைப்படை அடுக்குகள் மட்டும் கொண்ட பல்லுறுப்புக்கோவைச் சமன்பாடுகள் (Polynomial equations with Even Powers Only)

2n படியுள்ள P(x) எனும் பல்லுறுப்புக்கோவைச் சமன்பாட்டில் x−ன் இரட்டைப்படை அடுக்குகள் மட்டுமே உள்ளது (அதாவது ஒற்றைப்படை அடுக்குகளின் கெழுக்கள் 0 ஆகும்) எனில் x2 = y என பிரதியிட y−ல் n−படி உள்ள பல்லுறுப்புக்கோவைச் சமன்பாடு கிடைக்கும்; இப்பல்லுறுப்புக்கோவை சமன்பாட்டிற்கு y1, y2, …. yn ஆகியவை மூலங்கள் என்க. இனி x2 = y, என n சமன்பாடுகளை மட்டும் கருதும்போது ஒவ்வொரு r−க்கும் x −க்கு இரு மதிப்புகள் கிடைக்கும்; இந்த 2n மதிப்புகளே கொடுக்கப்பட்ட x−ல் உள்ள பல்லுறுப்புக்கோவைச் சமன்பாட்டிற்கு மூலங்களாக அமையும்.

எடுத்துக்காட்டு 3.16

x4 − 9x2 + 20 = 0 எனும் சமன்பாட்டைத் தீர்க்க.

தீர்வு

கொடுக்கப்பட்டுள்ள சமன்பாடு x4 − 9x2 + 20 = 0 ஆகும்.

இது ஒரு நாற்படிச் சமன்பாடாகும். x2 = y எனப் பிரதியிட y2 − 9y + 20 = 0 எனும் இருபடி சமன்பாடு கிடைக்கிறது. இதன் தீர்வு 4 மற்றும் 5 ஆகும். இனி x2 = 4 மற்றும் x2 = 5 என எடுத்துக் கொண்டால், கொடுக்கப்பட்ட சமன்பாட்டிற்கு 2, −2, √5, −√5 என்பது தீர்வுகளாகும்.

மேற்கண்ட வழிமுறையை, x6 − 17x3 + 30 = 0, ax2k + bxk + c = 0 மற்றும் பல்லுறுப்புக் கோவைச் சமன்பாடுகளுக்கும் மற்றும் anxkn + an−1xk(n−1) + ... + a1xk + a0 (இங்கு k என்பது ஏதேனும் ஒரு முழு எண்) என்ற முறையில் அமையும் பொதுவான பல்லுறுப்புக்கோவை சமன்பாட்டிற்கும் பயன்படுத்தலாம் என்பது குறிப்பிடத்தக்கது.

3. அனைத்து கெழுக்களின் கூட்டல்தொகை பூச்சியமாகும் (Zero Sum of all Coefficients)

P(x) = 0 எனும் ஒரு பல்லுறுப்புக்கோவைச் சமன்பாட்டின் கெழுக்களின் கூடுதல் பூச்சியம் என்க. கெழுக்களின் கூட்டல்தொகை என்பது உண்மையில் என்ன? கெழுக்களின் கூட்டல் என்பது P(1) என அறிவோம். எனவே கெழுக்களின் கூடுதல் பூச்சியம் எனில் P(1) = 0 என்பதால் P(x)−ன் ஒரு மூலம் 1 ஆகும். இனி மீதமுள்ள சமன்பாட்டின் தீர்வு காண்பது எளிதாகும்.

எடுத்துக்காட்டு 3.17

x3 − 3x2 – 33x + 35 = 0 என்ற சமன்பாட்டைத் தீர்க்க.

தீர்வு

இங்கு பல்லுறுப்புக் கோவை சமன்பாட்டின் கெழுக்களின் கூடுதல் பூச்சியமாகும். எனவே பல்லுறுப்புக்கோவை சமன்பாட்டின் ஒரு மூலம் 1 ஆகும். மீதமுள்ள மூலங்களைக் கண்டறிய x3 − 3x2 – 33x + 35 −ஐ x − 1ஆல் வகுக்க, x2 − 2x − 35 என்பது ஈவாகக் கிடைக்கின்றது. இதனைத் தீர்க்க 7 மற்றும் −5 மூலங்களாகும். எனவே 1,7,−5 ஆகியவை கொடுக்கப்பட்ட சமன்பாட்டிற்கு தீர்வு ஆகும்.

4. ஒற்றைப்படி உறுப்புகளின் கெழுக்களின் கூடுதலும் இரட்டைப் படி உறுப்புகளின் கெழுக்களின் கூடுதலும் சமம் (Equal Sums of Coefficients of Odd and Even Powers)

ஒற்றைப்படியுள்ள உறுப்புகளின் கெழுக்களின் கூடுதலும் இரட்டைப் படியுள்ள உறுப்புகளின் கெழுக்களின் கூடுதலும் சமமாக இருக்கும் ஒரு பல்லுறுப்புக்கோவைச் சமன்பாடு P(x) = 0 என்க. இவ்வாறு உரைப்பதன் பொருள் என்ன? a என்பது P(x) = 0 −ல் ஒற்றைப் படியிலுள்ள உறுப்பின் கெழு எனில் P(−x) = 0 −ல், அதே ஒற்றைப் படியிலுள்ள உறுப்பின் கெழு −a என இருக்கவேண்டும். P(x) = 0 மற்றும் P(−x) = 0 −ல் உள்ள இரட்டைப்படை படியிலுள்ள உறுப்புகளின் கெழுக்கள் சமமாக இருக்க வேண்டும். எனவே கொடுக்கப்பட்ட நிபந்தனையின்படி P(−x) = 0 −ல் உள்ள அனைத்து கெழுக்களின் கூடுதல் பூச்சியமாக இருக்கும். எனவே P(−x) = 0 −ன் ஒரு மூலம் 1 ஆகும். ஆகையால் P(x) = 0−ன் ஒரு மூலம் −1 ஆகும். இனி மீதி சமன்பாட்டு கணக்கைத் தீர்ப்பது மிகவும் எளிதாகும்.

எடுத்துக்காட்டு 3.18

2x3 +11x2 − 9x −18 = 0 என்ற சமன்பாட்டைத் தீர்க்க.

தீர்வு

இங்கு ஒற்றைப் படியுள்ள உறுப்புகளின் கெழுக்களின் கூடுதலும் இரட்டைப் படியுள்ள உறுப்புகளின் கெழுக்களின் கூடுதலும் சமமாக இருக்கின்றது. எனவே, −1 என்பது இச்சமன்பாட்டின் ஒரு மூலமாகும். இனி பிற மூலங்களைக் கண்டறிய 2x3 + 11x2 − 9x – 18 −ஐ x + 1ஆல் வகுத்து 2x2 + 9x − 18 என்பதை ஈவாகப் பெறுகிறோம். இதனைத் தீர்ப்பதன் மூலம், 3/2 மற்றும் −6 ஆகியவற்றை மூலங்களாக பெறுகிறோம். எனவே கொடுக்கப்பட்ட சமன்பாட்டிற்கு −6, −1, 3/2 ஆகியவை தீர்வுகளாக அமையும்.

5. தொடர்முறையில் உள்ள மூலங்கள் (Roots in Progressions)

உயர்படி பல்லுறுப்புக்கோவைச் சமன்பாடுகளைத் தீர்க்க முன்னரே குறிப்பிட்டது போல பல்லுறுப்புக்கோவைகளை பற்றியோ அல்லது சமன்பாட்டின் தீர்வுகளை பற்றியோ சில விவரங்கள் கூடுதலாகத் தேவைப்படும். "மூலங்கள் கூட்டுத்தொடர் முறையாக உள்ளன", “மூலங்கள் பெருக்குத்தொடர் முறையாக உள்ளன" என்பவை அத்தகைய சில விவரங்களாகும். இவ்வாறான சமன்பாடுகளில் ஒன்றைப் பற்றி இங்கு ஆராய்வோம்.

எடுத்துக்காட்டு 3.19

x3 + px2 + qx + r = 0 −ன் மூலங்கள் கூட்டுத் தொடர்முறையில் இருப்பதற்கான நிபந்தனையைப் பெறுக. 

தீர்வு

மூலங்கள் கூட்டுத்தொடரில் உள்ளன என்க. பின்னர் அம்மூலங்கள் a − d , a , a + d ஆகும். வியட்டாவின் சூத்திரத்தைப் பயன்படுத்த, நாம் பெறுவது

(a − d) + a + (a + d) = − p/1 = p ⇒ 3α =  −p ⇒ α =  −p/3 .

ஆனால், கொடுக்கப்பட்ட சமன்பாட்டிற்கு α ஒரு மூலம் என்பதால்,

(−p/3)3 + p(−p/3)2  + q(−p/3)  + r = 0 ⇒ 9pq = 2p3 + 27r இதுவே, கொடுக்கப்பட்ட சமன்பாட்டின் மூலங்கள் கூட்டுத் தொடர் அமையத் தேவையான நிபந்தனையாகும்.

எடுத்துக்காட்டு 3.20

ax3 + bx2 + cx + d = 0 எனும் சமன்பாட்டின் மூலங்கள் பெருக்குத் தொடர்முறையில் இருப்பதற்கான நிபந்தனையைக் காண்க. இங்கு a, b, c, d ≠ 0 எனக்கொள்க.

தீர்வு

மூலங்கள் பெருக்குத் தொடர்முறையில் உள்ளன என்க. எனவே, அவற்றை α/λ, α, αλ எனக் கருதுக.

வியட்டாவின் சூத்திரங்களைப் பயன்படுத்த நமக்குக் கிடைப்பது

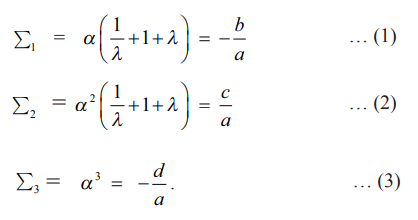
சமன்பாடு (2)−ஐ சமன்பாடு (1)−ஆல் வகுக்க,

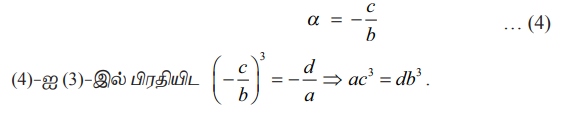
எடுத்துக்காட்டு 3.21

x4 + px2 + qx + r = 0 −ன் மூலங்கள் இசைத்தொடர் முறையில் உள்ளன எனில், 9pqr = 27r2 +2q3 என நிரூபிக்க. இங்கு p, q, r ≠ 0 என்க.

தீர்வு

மூலங்கள் இசைத் தொடர்முறையில் உள்ளன என்க. எனவே அவற்றின் பெருக்கல் தலைகீழிகள் கூட்டுத் தொடர் முறையில் இருக்கும். மேலும்,

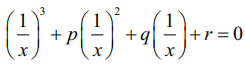  ⇔ rx3 + qx2 + px + 1 = 0 ……... (1)

(1) −ன் மூலங்கள் கூட்டுத்தொடர் முறையில் இருப்பதால் அவற்றினை a − d, a, a + d என்க. வியட்டாவின் சூத்தரங்களைப் பயன்படுத்த,

∑1 = (α − d) + α + (α + d) = −q/r ⇒ 3α = − q/r ⇒ α = − q/3r .

ஆனால் (1)−ன் மூலம் α என்பதால்,

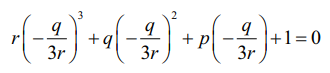⇒ −q3 + 3q3 − 9pqr + 27r2 = 0 ⇒ 9pqr = 2q3 +27r2.

எடுத்துக்காட்டு 3.22

x3 − 6x2 − 4x + 24 = 0 என்ற சமன்பாட்டின் மூலங்கள் கூட்டுத் தொடர் முறையாக உள்ளது என அறியப் படுகிறது. சமன்பாட்டின் மூலங்களைக் காண்க.

தீர்வு

மூலங்கள் a − d, a, a + d என்க. எனவே மூலங்களின் கூடுதல் 3a என்பது கொடுக்கப்பட்ட சமன்பாட்டின்படி 6−க்கு சமம். எனவே 3a = 6 ஆகும். ஆகையால் a = 2 ஆகும். மூலங்களின் பெருக்கல் a3 – ad2 என்பது சமன்பாட்டின்படி −24 −க்கு சமம். a −ன் மதிப்பைப் பிரதியிட 8 – 2d2 = −24  என ஆகும். எனவே, d = ±4 ஆகும். d = 4 எனில் –2, 2, 6 என மூலங்கள் கிடைக்கும். மேலும் d = −4 எனில், 6, 2, −2 (அதே மூலங்கள் பின்னோக்கு வரிசையில்) என மூலங்கள் கிடைக்கும்.