தலைகீழ் சமன்பாடுகள் (Reciprocal Equations)

2. தலைகீழ் சமன்பாடுகள் (Reciprocal Equations)

2x6 − 3x5 + √2x4 + 7x3 + √2x2 − 3x + 2 = 0.      …………….(1)

என்ற சமன்பாட்டின் ஒரு தீர்வு a என்க. இங்கு a ≠ 0 என்பது தெளிவு. இனி, 

 2α6 − 3α5 + √2α4 + 7α3 + √2α2 − 3α + 2 = 0.      

(1) −ன் இடப்பக்கத்தில் x −க்கு 1/α எனப் பிரதியிட

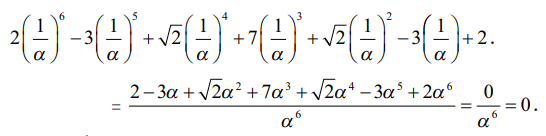
எனவே, 1/α என்பது (1)−க்கு ஒரு தீர்வாகிறது. இதே போன்று

2x5 + 3x4 − 4x3 + 4x2 − 3x − 2 = 0      …………….(2)

சமன்பாடு (2)−க்கு α ஒரு தீர்வு எனில், 1/α −ம் ஒரு தீர்வு ஆகும்.

(1) மற்றும் (2) சமன்பாடுகளுக்குள் இருக்கும் பொதுவான பண்பு என்னவெனில், சமன்பாட்டில் x −ஐ 1/x ஆல் பிரதியிட்டால் அதே சமன்பாடு மீண்டும் கிடைக்கும். உடனடியாக நம் மனதில் எழும் கேள்வியே "கொடுக்கப்பட்ட சமன்பாட்டைப் பார்த்தவுடன் அது மேற்கண்ட பண்பைப் பெற்றிருக்கின்றதா இல்லையா என்பதை இனம் காண்பது எவ்வாறு?" இவ்வினாவிற்கு தேற்றம் 3.6 விடையளிக்கிறது.

வரையறை 3.1

n−படி உள்ள P(x) எனும் ஒரு பல்லுறுப்புக்கோவை தலைகீழி பல்லுறுப்புக்கோவை எனில், கீழ்க்காணும் கூற்றுகளில் ஒன்று மெய்யாகும்.

(i) P(x) = xn P(1/x)

(ii) P(x) = −xnP(1/x)

n −படி உள்ள P(x) எனும் ஒரு பல்லுறுப்புக்கோவை, P(x) = xn P(1/x) என இருந்தால் முதல் வகை தலைகீழ் சமன்பாடு எனப்படும்.

n−படி உள்ள P(x) எனும் ஒரு பல்லுறுப்புக்கோவை, P(x) = − xn P(1/x) என இருந்தால் இரண்டாம் வகை தலைகீழ் சமன்பாடு எனப்படும்.

தேற்றம் 3.6

(i) an = a0 , an−1 = a1 , an−2 = a2 … (ii) an = −a0 , an−1 = −a1 , an−2 = −a2 … என்ற கூற்றுகளில் ஒன்று மெய் எனில், anxn + an−1xn−1 + an−2xn−2  + ... + a2x2 + a1x + a0 = 0 (இங்கு a ≠ 0) என்ற பல்லுறுப்புக்கோவைச் சமன்பாடு தலைகீழி பல்லுறுப்புக்கோவைச் சமன்பாடு எனப்படும். இதன் மறுதலையும் உண்மை.

நிரூபணம்

பல்லுறுப்புக்கோவைச் சமன்பாடு

P(x) = anxn + an−1xn−1 + an−2xn−2  + ... + a2x2 + a1x + a0 = 0  …………..(1)

(1) −ல் x −ஐ 1/x −ஆல் பிரதியிட்டால்,

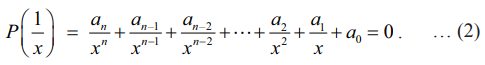
எனக் கிடைக்கும். (2)−ன் இருமருங்கும் xn −ஆல் பெருக்க,

xnP(1/ x) = a0xn + a1xn−1 + a2xn−2  + ... + an−2x2 + an−1x + an = 0  …………..(3)

எனக் கிடைக்கும். இனி (1) என்பது தலைகீழ் சமன்பாடு ⇔ P(x) = ± xnP(1/ x) ⇔  (1) மற்றும் (3) ஆகிய இரு சமன்பாடுகளும் ஒன்றேயாகும்.

இது சாத்தியம்,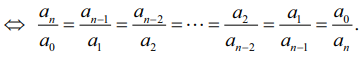

என இருக்கவேண்டும். இங்கு விகிதாச்சாரம் λ என்க. எனவே, an / a0 = λ மற்றும் a0 / an = λ எனக் கிடைக்கிறது. இவ்விரு சமன்பாடுகளையும் பெருக்கினால், λ2 = 1எனக் கிடைக்கிறது. எனவே, λ = 1 மற்றும் λ = −1 என இரு நிலைகள் கிடைக்கின்றன.

நிலை (i) : 

λ =1 இந்நிலையில் an = a0 , an−1 = a1 , an−2 = a2, … எனக் கிடைக்கிறது. அதாவது, (1)−ல் முதலிலிருந்தும் கடைசியிலிருந்தும் சமதூரத்தில் உள்ள கெழுக்கள் சமமாக உள்ளன.

நிலை (ii) :

λ = −1 இந்நிலையில் an = −a0 , an−1 = −a1 , an−2 = −a2 … எனக் கிடைக்கிறது. அதாவது, சமன்பாடு (1) −ல் முதலிலிருந்தும் கடைசியிலிருந்தும் சமதூரத்தில் உள்ள கெழுக்கள் எண்ணளவில் சமமாகவும் மற்றும் எதிர் குறியையும் பெற்றிருக்கும்.

குறிப்பு

முதல்வகை தலைகீழ் சமன்பாடுகளில் கெழுக்கள் முதலில் இருந்தும் (இறுதியில் இருந்தும்) சமமாக உள்ளன. உதாரணத்திற்கு, 6x5 + x4 − 43x3 − 43x2  + x + 6 = 0 எனும் சமன்பாடு முதல்வகை தலைகீழ் சமன்பாடாகும்.

இரண்டாம்வகை தலைகீழ் சமன்பாடுகளில் கெழுக்கள் முதலில் இருந்தும் (இறுதியில் இருந்தும்) எண்ணளவில் சமமாகவும் குறிகள் நேர் எதிராகவும் உள்ளன. உதாரணத்திற்கு, 6x5 − 41x4 + 97x3 − 97x2 + 41x − 6 = 0 எனும் சமன்பாடு இரண்டாம் வகை தலைகீழ் சமன்பாடாகும்.

குறிப்புரை

(i) தலைகீழ் சமன்பாட்டிற்கு 0 ஒரு தீர்வாகாது.

(ii) கெழுக்களும் தீர்வுகளும் மெய்யெண்கள் வரம்பிற்குள் உட்படுத்தப்படவில்லை

(iii) “ P(x) = 0 எனும் பல்லுறுப்புகோவை சமன்பாட்டில் எப்பொழுதெல்லாம் α ஒரு மூலமாகிறதோ அப்பொழுதெல்லாம் 1/α −ம் ஒரு மூலமாக இருக்கும் பல்லுறுப்புக்கோவைச் சமன்பாடு தலைகீழ் பல்லுறுப்புக்கோவை சமன்பாடாகத்தான் இருக்கவேண்டும்" என்ற கூற்று உண்மையல்ல. உதாரணமாக 2x3 − 9x2 + 12x – 4 = 0 என்ற பல்லுறுப்புக்கோவைச் சமன்பாட்டின் மூலங்கள் 2,2, 1/2 ஆகும். x3P(1/x) ≠ ±P(x) என்பதால், இச்சமன்பாடு தலைகீழ் சமன்பாடாகாது. தலைகீழ் சமன்பாடுகள் an−r = ar அல்லது an−r = −ar என்பதைப் பொறுத்து முதல்வகை மற்றும் இரண்டாம் வகை என இரு வகைப்படும். நிரூபணமின்றி சில முடிவுகள் இங்கு தரப்படுகிறது.:

• முதல்வகை சார்ந்த ஓர் ஒற்றைப் படை படி தலைகீழ் சமன்பாட்டிற்கு, x =−1 ஒரு தீர்வாகும். 

• இரண்டாம்வகை சார்ந்த ஓர் ஒற்றைப் படை படி தலைகீழ் சமன்பாட்டிற்கு, x = 1 ஒரு தீர்வாகும்.

• இரண்டாம்வகை சார்ந்த ஓர் இரட்டைப் படை படி தலைகீழ் சமன்பாட்டிற்கு, மைய உறுப்பு பூச்சியமாகத் தான் இருக்கும். மேலும் x = 1 மற்றும் x = −1 தீர்வுகளாகும்.

• இரட்டைப்படை தலைகீழ் சமன்பாடுகளில் x + 1/x அல்லது x − 1/x ஐ, y எனப் பிரதியிட, கொடுக்கப்பட்ட பல்லுறுப்புக்கோவை சமன்பாட்டின் படி மதிப்பில் பாதி படியாக ஒரு பல்லுறுப்புக்கோவை சமன்பாட்டைப் பெறுகிறோம். இப்பல்லுறுப்புக்கோவை சமன்பாட்டை தீர்ப்பதன் மூலம் தேவையான பல்லுறுப்புக்கோவை சமன்பாட்டிற்கான மூலங்கள் பெற இயலும். 

எடுத்துக்காட்டாக,

6x6 − 35x5 + 56x4 − 56x2 + 35x – 6 = 0

என்பது இரட்டைப்படை இரண்டாம் வகை தலைகீழ் சமன்பாடாகும். எனவே 1 மற்றும் −1 ஆகியவை சமன்பாட்டின் இரு தீர்வுகள் என்பதால் x2 − 1 என்பது பல்லுறுப்புக் கோவையின் ஒரு காரணியாகும். எனவே பல்லுறுப்புக்கோவையை x2 – 1 −ஆல் வகுக்க, 6x4 − 35x3 + 62x2 − 35x + 6 என ஒரு காரணி கிடைக்கிறது. இக்காரணியை x2 −ஆல் வகுத்து உறுப்புகளை ஒழுங்குபடுத்த 6(x2 + 1/x2) – 35(x + 1/x) + 62 எனக்கிடைக்கிறது u = (x + 1/x) எனப் பிரதியிட, சமன்பாடு 6(u2 – 2) – 35u + 62 = 0 என இருபடி சமன்பாடாகிறது.மேலும் 6u2 − 35u + 50 = 0 என எளிமைபடுத்தப் படுகிறது. இதனைத் தீர்க்க u =10/3 = 5/2 எனக் கிடைக்கிறது. u = 10/3 என்பதன் மூலம், x = 3, 1/3 என்ற மதிப்புகளும் u = 5/2 என்பதன் மூலம் x = 2, 1/2 என்ற மதிப்புகளும் கிடைக்கிறது.எனவே +1, −1, 2, ½, 3 , 1/3 ஆகியவை தீர்வுகளாக அமைகின்றன.

எடுத்துக்காட்டு 3.27

7x3 − 43x2 = 43x −7 என்ற சமன்பாட்டைத் தீர்க்க. 

தீர்வு

கொடுக்கப்பட்ட சமன்பாட்டை 7x3 − 43x2 − 43x + 7 = 0 என மாற்றி எழுதலாம். இது முதல்வகையைச் சார்ந்த ஒற்றைப்படை படி தலைகீழ் சமன்பாடு. எனவே −1 ஒரு தீர்வாகும். ஆகையால் x + 1 ஒரு காரணியாகும். 7x3 − 43x2 − 43x + 7 என்ற பல்லுறுப்புக்கோவையை x + 1 ஆல் வகுக்க 7x2 − 50x + 7 எனும் ஒரு காரணி கிடைக்கிறது. இதனைத் தீர்க்க 7 மற்றும் 1/7 மூலங்களாகக் கிடைக்கிறது. எனவே கொடுக்கப்பட்ட சமன்பாட்டிற்கு −1, 1/7, 7 தீர்வுகளாக அமையும்.

எடுத்துக்காட்டு 3.28

x4 − 10x3 + 26x2 −10x + 1 = 0 என்ற சமன்பாட்டைத் தீர்க்க.

தீர்வு

இது இரட்டைப்படை முதல் வகை தலைகீழ் சமன்பாடாகும். எனவே இதனை,

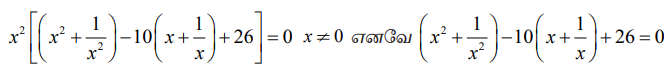
என மாற்றி எழுதலாம். y = (x + 1/x) என்க.

[(y2 − 2) −10y + 26] = 0 ⇒ (y2 −10y + 24) = 0 ⇒ (y − 6) ( y −4) = 0.

நிலை (i)

y = 6 எனில்,  x + 1/x = 6 ⇒ x = 3 + 2√2, x = 3 − 2√2.

நிலை (ii)

y = 4 எனில், x + 1/x = 4 ⇒ x = 2 + √3, x = 2 − √3.

எனவே, மூலங்கள் 3 ± 2√2, 2 ± √3 ஆகும்.