சமன்பாட்டியல் - இருபடிச் சமன்பாட்டிற்கான வியட்டாவின் சூத்திரங்கள் (Vieta's formula for Quadratic Equations) | 12th Maths : UNIT 3 : Theory of Equations
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 3 : சமன்பாட்டியல்
இருபடிச் சமன்பாட்டிற்கான வியட்டாவின் சூத்திரங்கள் (Vieta's formula for Quadratic Equations)
வியட்டாவின் சூத்திரங்கள் மற்றும் பல்லுறுப்புக் கோவைச் சமன்பாடுகளை உருவாக்குதல் (Vieta's Formulae and Formation of Polynomial Equations)
ஒரு பல்லுறுப்புக்கோவையின் கெழுக்கள் அவற்றின் மூலங்களின் கூடுதல் மற்றும் மூலங்களின் பெருக்கல் இவற்றை தொடர்புபடுத்தும் சூத்திரமே வியட்டாவின் சூத்திரமாகும். பல்லுறுப்புக் கோவையில் பிரெஞ்சு கணிதவியலாளரான வியட்டாவின் பங்கு நவீன இயற்கணிதத்திற்கு வழிகோலியது.
1. இருபடிச் சமன்பாட்டிற்கான வியட்டாவின் சூத்திரங்கள் (Vieta's formula for Quadratic Equations)
ax2 + bx + c = 0 எனும் இருபடி சமன்பாட்டின் மூலங்கள் α மற்றும் β என்க.
பின்னர்,
ax2 + bx + c = a(x − α)(x − β) = ax2 − a(α + β)x + a(α β).
ஒத்த அடுக்குகளின் கெழுக்களை ஒப்பிடும்போது, α + β = − b/a . மற்றும் αβ = c/a என கிடைக்கின்றது. எனவே α மற்றும் β ஆகியவற்றை மூலங்களாகக் கொண்ட ஒரு இருபடிச் சமன்பாடு x2 − (α + β)x + αβ = 0 ஆகும். அதாவது, கொடுக்கப்பட்ட மூலங்களைக் கொண்ட இருபடிச் சமன்பாடு
x2 − (மூலங்களின் கூடுதல்) x + (மூலங்களின் பெருக்கல்) = 0 ……………(1)
குறிப்பு
மேற்கண்ட கூற்றில், ஒருமைச் சொல்லான 'ஒரு' பயன்படுத்தப்பட்டுள்ளது. உண்மையில் P(x) = 0 எனும் இருபடிச் சமன்பாட்டின் மூலங்கள் α மற்றும் β எனில் c எனும் பூச்சியமற்ற மாறிலிக்கு, cP(x) என்பதும் α மற்றும் β ஆகியவற்றை மூலங்களாகக் கொண்ட இருபடிச் சமன்பாடாகும்.
கெழுக்களுக்கும் மூலங்களுக்கும் இடையே உள்ள தொடர்புகளைப் பயன்படுத்தி முந்தைய வகுப்புகளில் α மற்றும் β மூலங்களாக உடைய இருபடிச்சமன்பாட்டை உருவாக்கினோம். உண்மையில் அத்தகைய சமன்பாட்டில் ஒன்றுதான் சமன்பாடு (1)−ல் தரப்பட்டுள்ளது. எடுத்துக்காட்டாக, 3 மற்றும் 4 ஆகியவற்றை மூலங்களாகக் கொண்ட ஒரு இருபடிச்சமன்பாடு x2 − 7x + 12 = 0 ஆகும்.
மேலும் கொடுக்கப்பட்ட பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்களின் சார்புகளை மூலங்களாகக் கொண்ட புதிய பல்லுறுப்புக் கோவை சமன்பாட்டை உருவாக்கலாம். இந்த முறையில் கொடுக்கப்பட்ட பல்லுறுப்புக் கோவைச் சமன்பாட்டின் மூலங்களைக் காணாமலேயே புதிய பல்லுறுப்புக் கோவைச் சமன்பாட்டை உருவாக்கலாம். எடுத்துக்காட்டாக, கொடுக்கப்பட்ட ஒரு பல்லுறுப்புக் கோவைச்சமன்பாட்டின் மூலங்களுடன் 2−ஐ கூட்டுவதன் மூலம் புதிய பல்லுறுப்புக் கோவை சமன்பாட்டை பின்வருமாறு உருவாக்குவோம். (பார்க்க எடுத்துக்காட்டு 3.1).
எடுத்துக்காட்டு 3.1
17x2 + 43x − 73 = 0 எனும் இருபடிச் சமன்பாட்டின் மூலங்கள், α மற்றும் β எனில் α + 2 மற்றும் β + 2 என்பவற்றை மூலங்களாகக் கொண்ட ஒரு இருபடிச்சமன்பாட்டை உருவாக்கவும்.
தீர்வு
17x2 + 43x – 73 = 0 எனும் இருபடிச் சமன்பாட்டின் மூலங்கள், α மற்றும் β என்பதால்,
α + β = −43/17 மற்றும் αβ = −73/17 ஆகும்.
தேவையான இருபடிச் சமன்பாட்டின் மூலங்கள் α + 2 மற்றும் β + 2 ஆகும். எனவே,
மூலங்களின் கூடுதல் = α + β + 4 = −43/17 + 4 = 25/17
மூலங்களின் பெருக்கல் = α β + 2(α + β) + 4 = −73/17 + 2(−43/17) + 4 = −91/17
எனவே, தேவையான இருபடிச் சமன்பாடு x2 − 25/17 x − 91/17 = 0 ஆகும். இச்சமன்பாட்டை 17 −ஆல் பெருக்க, α + 2 மற்றும் β + 2 ஆகியவற்றை மூலங்களாகக் கொண்ட 17x2 − 25x − 91 = 0 எனும் இருபடிச் சமன்பாடு கிடைக்கிறது.
எடுத்துக்காட்டு 3.2
2x2 −7x + 13 = 0 எனும் இருபடிச் சமன்பாட்டின் மூலங்கள் α மற்றும் β எனில் α2 மற்றும் β 2 ஆகியவற்றை மூலங்களாகக் கொண்ட ஒரு இருபடிச் சமன்பாட்டை உருவாக்கவும்.
தீர்வு
கொடுக்கப்பட்ட இருபடிச் சமன்பாட்டின் மூலங்கள் α மற்றும் β என்பதால், α + β = 7/2 மற்றும் αβ = 13/2 ஆகும்.
எனவே, தேவையான இருபடிச் சமன்பாட்டை பெற,
மூலங்களின் கூடுதல் = α2 + β 2 = (α + β) 2 − 2α β = −3/4
மூலங்களின் பெருக்கல் = α2β 2 = (α β) 2 = 169/4
எனவே, தேவையான இருபடிச் சமன்பாடு x2 + 3/4x + 169/4 = 0 எனக்கிடைக்கிறது.
4x2 + 3x + 169 = 0
இதுவே α2 மற்றும் β2 ஆகியவற்றை மூலங்களாகக் கொண்ட இருபடிச் சமன்பாடாகும்
குறிப்புரை
எடுத்துக்காட்டு 3.1 மற்றும் 3.2−லிருந்து α + β மற்றும் αβ மதிப்புகளைப் பயன்படுத்தி மூலங்களின் கூடுதல் மற்றும் பெருக்கல் தொகையைக் கணித்தோம். இவ்வாறு கொடுக்கப்பட்ட இருபடிச் சமன்பாட்டின் மூலங்களின் கூடுதல் மற்றும் பெருக்கலைக் கொண்டு தேவையான இருபடிச் சமன்பாட்டின் மூலங்களின் கூடுதல் மற்றும் பெருக்கலை கணக்கிட்டுத் தேவையான இருபடிச்சமன்பாட்டை உருவாக்க இயலும். இங்கு கொடுக்கப்பட்ட சமன்பாட்டின் தீர்வு காணவில்லை என்பது குறிப்பிடத்தக்கது. பல்லுறுப்புக் கோவை சமன்பாட்டை உருவாக்கும் பணி முடிவடைந்த பின்னர் கூட α மற்றும் β மதிப்பு நமக்குத் தெரிவதில்லை.
2. பல்லுறுப்புக் கோவைச் சமன்பாடுகளுக்கான வியட்டாவின் சூத்திரங்கள் (Vieta's formula for Polynomial Equations)
இருபடி பல்லுறுப்புக்கோவைகள் பற்றி அறிந்ததை மேலும் உயர் படி பல்லுறுப்புக்கோவைகளுக்கு நீட்டிக்கலாம். இப்பாடப்பகுதியில் உயர்படி பல்லுறுப்பு கோவைகளின் பூச்சியங்களாக்கிகளுக்கும் அதன் கெழுக்களுக்கும் உள்ள தொடர்பினைப் பற்றி கற்போம். பல்லுறுப்புக் கோவையின் பூச்சியங்களாக்கிகளைப் பற்றி சில தகவல்கள் தெரிந்திருந்தால் உயர்படி பல்லுறுப்புக்கோவைகளை உருவாக்குவது எப்படி என்பதைப் பற்றிக் கற்போம். இப்பாடப்பகுதியில் n படியுள்ள பல்லுறுப்புக் கோவையின் பூச்சியங்களாக்கிகளையோ அல்லது n படியுள்ள பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்களையோ பயன்படுத்துவோம்.
(a) அடிப்படை இயற்கணிதத் தேற்றம் (The Fundamental Theorem of Algebra)
P(x) = 0 எனும் பல்லுறுப்புக்கோவை சமன்பாட்டின் ஒரு மூலம் a எனில் (x − a) என்பது P(x) −ன் ஒரு காரணியாகும். எனவே P(x) −ன் படி ≥ 1 ஆகும். a மற்றும் b என்பவை P(x) = 0 −ன் மூலங்கள் எனில், (x − a)(x − b) என்பது P(x) −ன் ஒரு காரணியாகும். ஆகையால், P(x) −ன் படி ≥ 2 எனக் கூறலாம். இவ்வாறே, P(x) = 0 −க்கு n மூலங்கள் இருந்தால், அதன் படி n ஆகவோ அல்லது அதற்கு மேற்பட்டோ இருக்கவேண்டும். அதாவது, n படி உள்ள ஒரு பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்கள் n−க்கு மேற்பட்டு இருக்காது.
முந்தைய வகுப்புகளில் "மடங்கெண்" பற்றி கற்றதை நினைவில் கொள்வோம். P எனும் பல்லுறுப்புக்கோவை சமன்பாட்டிற்கு (x − a)k என்பது ஒரு காரணியாகவும் (x − a)k+l காரணியாக இல்லாமலும் அமைந்தால், a எனும் மூலத்தின் மடங்கெண் k என்று அழைக்கப்படும். உதாரணமாக x2 − 6x + 9 = 0 மற்றும் x3 − 7x2 + 159x – 9 = 0 ஆகிய பல்லுறுப்புக்கோவைச் சமன்பாடுகளுக்கு 3 எனும் மூலத்தின் மடங்கெண் 2 ஆகும். இங்கு கலப்பெண்களை நாம் கெழுக்களாகப் பயன்படுத்தவில்லை என்றாலும் x2 − (4 + 2i)x + 3 + 4i மற்றும் x4 − 8x3 + 26x2 − 40x + 25 = 0 என்ற பல்லுறுப்புக்கோவைச் சமன்பாடுகளுக்கு 2 + i எனும் மூலத்தின் மடங்கெண் 2 ஆகும். ஒரு பல்லுறுப்புக்கோவை சமன்பாட்டின் a எனும் மூலத்தின் மடங்கெண் 1 என்றால், a என்பது பல்லுறுப்புக் கோவை சமன்பாட்டின் எளிய மூலம் என அழைக்கப்படும்.
P(x) = 0 −க்கு மடங்கெண்ணையும் சேர்த்து n மூலங்கள் இருந்தால், அப்போதும் கூட படி n −க்குச் சமமாகவோ அல்லது அதைவிட அதிகமாகவேதான் இருக்கும் எனக் காண்கிறோம். வேறு வார்த்தைகளில் சொல்வதென்றால் “n படியுள்ள ஒரு பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்களுடன் மடங்கெண்ணையும் சேர்த்து கணக்கிட்டாலும் அச்சமன்பாட்டிற்கு n மூலங்களுக்கு மேல் இராது" எனலாம்.
சமன்பாட்டியலிலேயே மிகவும் முக்கியத்துவம் வாய்ந்த தேற்றங்களில் ஒன்று அடிப்படை இயற்கணிதத் தேற்றமாகும். அதன் நிரூபணம் இந்நூலின் பாடத்திட்டத்திற்கு அப்பாற்பட்டது என்பதால் தேற்றத்தின் கூற்று நிரூபணமின்றித் தரப்பட்டுள்ளது.
தேற்றம் 3.1 (அடிப்படை இயற்கணிதத் தேற்றம்) (The Fundamental Theorem of Algebra)
படி n ≥ 1 என உள்ள ஒவ்வொரு பல்லுறுப்புக்கோவை சமன்பாட்டிற்கும் குறைந்தபட்சம் ஒரு மூலமாவது ℂ −ல் இருக்கும்.
இத்தேற்றத்தின் கூற்று மூலமாக n படியுள்ள ஒரு பல்லுறுப்புக்கோவை சமன்பாட்டிற்கு மூலங்களின் மடங்கெண்ணையும் கணக்கில் எடுத்துக் கொண்டு குறைந்தபட்சம் n மூலங்கள் ℂ −ல் இருக்கும் என நிரூபிக்க இயலும். நமது விவாதத்தில் இந்த கூற்றையும் தொகுத்துக் கூறினால்
n படியுள்ள ஒரு பல்லுறுப்புக்கோவை சமன்பாட்டிற்கு ℂ −ல் சரியாக n மூலங்கள் அவற்றின் மடங்கெண்ணையும் கருத்தில் கொள்ளப்பட்டு அமையும்.
சில நூலாசிரியர்கள் மேற்கண்ட கூற்றைத்தான் அடிப்படை இயற்கணித தேற்றம் எனக் குறிப்பிடுவர்.
(b) வியட்டாவின் சூத்திரம் (Vieta's Formula)
(i) முப்படி பல்லுறுப்புக்கோவைச் சமன்பாட்டிற்கான வியட்டாவின் சூத்திரம் (Vieta's Formula for Polynomial equation of degree 3)
இனி இது போன்ற தொடர்புகளை உயர்படி பல்லுறுப்புக் கோவைகளுக்கும் விரிவுபடுத்தலாம். கீழ்க்காணும் முப்படி பல்லுறுப்புக் கோவை சமன்பாட்டை கருதுவோம்.
ax3 + bx2 + cx + d = 0.
அடிப்படை இயற்கணிதத் தேற்றத்தின்படி இதற்கு மூன்று மூலங்கள் உண்டு. அவை α, β மற்றும் γ என்க. எனவே,
ax3 + bx2 + cx + d = a(x − α)(x − β)(x − γ)
வலப்பக்கத்தை விரிவுபடுத்தி பின்வருமாறு எழுதலாம்.
ax3 + bx2 + cx + d = ax3 − a(α + β + γ)x2 + a(αβ + βγ + γα)x− a(α β γ).
ஒத்த அடுக்குகளின் கெழுக்களை ஒப்பிட,
α + β + γ = −b/a , αβ + βγ + γα = c/a மற்றும் αβγ = −d/a எனப் பெறலாம்.
பல்லுறுப்புக் கோவையின் படி 3 என்பதால், a ≠ 0 என்றிருக்க வேண்டும். இதனால் a −ஆல் வகுப்பது அர்த்தமுள்ளதாகும். ஒற்றை முப்படி பல்லுறுப்புக்கோவையின் மூலங்கள் முறையே α, β மற்றும் γ எனில்,
x2 −ன் கெழு = − (α + β + γ),
x2 −ன் கெழு = αβ + βγ + γα, மற்றும்
மாறிலி உறுப்பு = −αβγ .
(ii) படி n > 3 உடைய பல்லுறுப்புக் கோவை சமன்பாட்டிற்கான வியட்டாவின் சூத்திரம் (Vieta's Formula for Polynomial equation of degree n > 3)
மேற்க்கண்ட தொடர்புகள் n உயர்படி ஒற்றை பல்லுறுப்புக்கோவை சமன்பாட்டிற்க்கும் மெய்யாகும். ஒரு n படி உள்ள தலைஒற்றை பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்கள் a1, a2, ... , an எனில்,
xn−1−ன் கெழு = ∑1 = −∑ α1
xn−2−ன் கெழு = ∑2 = ∑ α1 α2
xn−3−ன் கெழு = ∑3 = −∑ α1 α2 α3
x −ன் கெழு = ∑n−1 = (−1)n−1∑ α1 α2 … αn−1
x0 −ன் கெழு = மாறிலி = ∑n = (−1)n α1 α2 … αn

இங்கு ∑α1 என்பது அனைத்து மூலங்களின் கூடுதல், ∑α1α2 என்பது அனைத்து மூலங்களையும் இரண்டிரண்டு மூலங்களாக எடுத்துக்கொண்டு பெருக்கிக் கிடைக்கும் மதிப்புகளின் கூட்டல் பலன், ∑ α1α2α3 என்பது அனைத்து மூலங்களையும் மும்மூன்றாக பெருக்கிக் கிடைக்கும் மதிப்புகளின் கூட்டல் பலன், எனத் தொடர்ச்சியாக இவ்வண்ணமே குறிப்பிட்டுச் சொல்லிக் கொண்டே போகலாம். எடுத்துக்காட்டாக, α , β , γ மற்றும் δ என்பன நாற்படி (சதுர்) பல்லுறுப்புக் கோவை சமன்பாட்டின் மூலங்கள் எனில், ∑ α1 என்பதை ∑ α என்றும், ∑ α1α2 என்பதை ∑ αβ எனவும் எழுதலாம்
ஆகவே,
∑ α = α + β + γ + δ
∑αβ = αβ + αγ + αδ + βγ + βδ + γδ
∑αβγ = αβγ + αβδ + αγδ + βγδ
∑αβγδ = αβγδ
மூலங்கள் வெளிப்படையான எண் வடிவத்தில் இருந்தாலும் இத்தகைய குறியீடுகளை வசதிக்காக பயன்படுத்துகிறோம்.
அதிக மடங்கெண் கொண்ட மூலங்களைக் கையாளும்போது கவனம் தேவை. உதாரணமாக ஒரு முப்படி பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்கள் 1, 2, 2, எனில், ∑α = 5 மற்றும் ∑αβ = (1×2) + (1 × 2) + (2 × 2) = 8.
மேற்கண்ட விவாதத்திலிருந்து, ஒரு தலைஒற்றை பல்லுறுப்புக்கோவை சமன்பாட்டிற்கு மூலங்களின் கூட்டற்பலன் என்பது xn−1 −ன் குணகத்தை (−1)−ஆல் பெருக்க கிடைக்கும் பெருக்கல் தொகையாகும். மேலும், மூலங்களின் பெருக்கற்பலன் என்பது மாறிலி உறுப்பை (−1)n −ஆல் பெருக்கக் கிடைப்பதாகும்.
எடுத்துக்காட்டு 3.3
α, β, γ என்பவை x3 + px2 + qx + r = 0 எனும் சமன்பாட்டின் மூலங்களாக இருந்தால், கெழுக்களின் அடிப்படையில் ∑ [ 1/βγ ] −ன் மதிப்பைக் காண்க.
தீர்வு
x3 + px2 + qx + r = 0 எனும் சமன்பாட்டின் மூலங்கள் a, β, மற்றும் 7 என்பதால்,
∑1 α + β + γ = −p மற்றும் ∑3 αβγ = −r
எனவே,
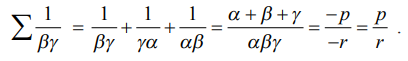
(c) கொடுக்கப்பட்ட மூலங்களை வைத்து பல்லுறுப்புக்கோவைச் சமன்பாடுகளை உருவாக்குதல் (Formation of Polynomial Equations with given Roots)
இருபடிச் சமன்பாட்டின் மூலங்கள் தெரிந்திருக்குமானால், அதன் சமன்பாட்டை அமைத்தோம். இப்பொழுது, மூலங்களை அறிந்திருந்தால் உயர்படி சமன்பாடுகளை எங்ஙனம் உருவாக்குவது என்பது பற்றி கற்போம். a1,a2, …. , an என்ற மூலங்களை உடைய ஒரு n படி பல்லுறுப்புக்கோவைச் சமன்பாட்டை எவ்வாறு காண்பது? காரணிகளின் பெருக்கற்பலனாக ஒரு பல்லுறுப்புக்கோவைச் சமன்பாட்டை எழுதுவது ஒரு வழி ஆகும். அதாவது, α1, α2, … αn என மூலங்களையுடைய ஒரு பல்லுறுப்புக்கோவைச் சமன்பாடு
(x − α1)(x – α2)(x – α3) ... (x – αn) = 0 ஆகும்.
ஆனால் இவ்வாறு ஒரு பல்லுறுப்புக்கோவைச் சமன்பாட்டை எழுதுவது வழக்கமல்ல. திட்ட வடிவத்தில் பல்லுறுப்புக்கோவைச் சமன்பாட்டை எழுத அதிக கணக்கீடுகள் தேவை. ஆனால் கெழுக்களுக்கும் மூலங்களுக்கும் உள்ளத் தொடர்பினைப் பயன்படுத்தி பல்லுறுப்புக்கோவைச் சமன்பாட்டை நேரடியாக நம்மால் எளிதாக எழுதிவிட இயலும். மேலும் முழுவதுமாக ஒரு பல்லுறுப்புக்கோவைச் சமன்பாட்டை உருவாக்காமலேயே எந்த ஒரு குறிப்பிட்ட அடுக்குள்ள x −ன் கெழுவையும் எழுதிவிட இயலும்.
மூலங்கள் α, β, மற்றும் γ உடைய ஒரு முப்படி பல்லுறுப்புக்கோவைச் சமன்பாடு
x3 − (α + β + γ)x2 + (αβ + βγ + γα)x − αβγ = 0 ஆகும்.
α1, α2, … αn மூலங்களாகக் கொண்ட n படியுள்ள ஒரு பல்லுறுப்புக்கோவை சமன்பாட்டை
xn – (∑ α1)xn−1 + (∑ α1 α2 )xn−2 − (∑ α1 α2 α3)xn−3 +... + (−1)n α1α2 … αn = 0 என எழுதலாம்.
இங்கு, ∑α1, ∑α1 α2 , ∑ α1α2α3 ,... ஆகியன முன்னரே வரையறுக்கப்பட்டவையாகும்.
உதாரணமாக, 1, −2 மற்றும் 3 ஆகிய மூலங்களைக் கொண்ட ஒரு பல்லுறுப்புக்கோவைச் சமன்பாடு
x3 − (1− 2 + 3)x2 + (1 × (−2) + (−2) × 3 + 3 × 1)x – 1 × (−2) × 3 = 0 ஆகும்.
இதனைச் சுருக்கும்போது x3 + 2x2 − 5x + 6 = 0 என்றாகும். (x −1)(x + 2)(x − 3) = 0 என்பதன் விரிவாக்கமே x3 + 2x2 − 5x + 6 = 0 என சரிபார்ப்பது ஆர்வமளிக்கக் கூடியதாகும்.
எடுத்துக்காட்டு 3.4
ax4 + bx3 + cx2 + dx + e = 0 −ன் மூலங்களின் வர்க்கங்களின் கூடுதல் காண்க. இங்கு a ≠ 0 ஆகும்.
தீர்வு
ax4 + bx3 + cx2 + dx + e = 0 −ன் மூலங்கள் α, β, γ மற்றும் δ என்க. எனவே,
∑1 = α + β + γ + δ = − b/a ,
∑2 = α β + α γ + α δ + β γ + β δ + γ δ = c/a ,
∑3 = α β γ + α β δ + α γ δ + β γ δ = − d/a ,
∑4 = αβγδ = e/a .
α2 + β2 + γ2 + δ2 −ன் மதிப்பைக் காணவேண்டுமெனில்,
(a + b + c + d)2 ≡ a2 + b2 + c2 + d2 + 2(ab + ac + ad + bc+ bd + cd)
எனும் முற்றொருமையினைப் பயன்படுத்த வேண்டும். எனவே,
α2 + β2 + γ2 + δ2 = (α + β + γ + δ)2 − 2(α β + α γ + α δ + β γ + β δ + γ δ)
= (− b/a)2 −2(c/a)
= (b2 −2ac)/ a2
எடுத்துக்காட்டு 3.5
x3 + ax2 + bx + c = 0 என்ற முப்படிச் சமன்பாட்டின் மூலங்கள் p : q : r எனும் விகிதத்தில் அமைய நிபந்தனையைக் காண்க.
தீர்வு
மூலங்கள் p : q : r எனும் விகிதத்தில் இருப்பதால், மூலங்களை, pλ, qλ மற்றும் rλ எனக் கொள்க. இனி,
∑1 = pλ + qλ + rλ = −a, ….. (1)
∑2 = = (pλ)(qλ) + (qλ)(rλ) + (rλ)(pλ) = b, ........(2)
∑3 = (pλ)(qλ)(rλ) = −c, …....(3)
(1) ⇒ λ = − a/ (p + q + r) …....(4)
(3) ⇒ λ3 = − c/pqr ...........(5)
(4) −ஐ (5)−ல் பிரதியிட, நமக்கு கிடைப்பது
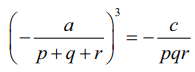 ⇒ pqra3 = c(p + q + r)3
⇒ pqra3 = c(p + q + r)3
எடுத்துக்காட்டு 3.6
x3 + ax2 + bx + c = 0 எனும் முப்படிச் சமன்பாட்டின் மூலங்களின் வர்க்கங்களை மூலங்களாகக் கொண்ட ஒரு சமன்பாட்டை உருவாக்குக.
தீர்வு
x3 + ax2 + bx + c = 0 எனும் முப்படிச் சமன்பாட்டின் மூலங்கள் α, β, மற்றும் γ என்க. எனவே,
∑1 = α + β + γ = − a , ….. (1)
∑2 = α β + β γ + γ α = b , ….. (2)
∑3 = αβγ = −c. ….. (3)
α2, β2, மற்றும் γ2 ஆகியவற்றை மூலங்களாகக் கொண்ட ஒரு சமன்பாட்டை உருவாக்க வேண்டும்.
(1), (2) மற்றும் (3) ஆகியவற்றைப் பயன்படுத்தி, பின்வருவனவற்றைக் கண்டறிவோம் :
∑1 = α2 + β2 + γ2 = (α + β + γ)2 − 2(α β + β γ + γ α) = (−a2) – 2(b) = a2 − 2b ,
∑2 = α2 β2 + β2 γ2 + γ2 α2 = (α β + β γ + γ α)2 − 2((α β)(β γ) + (β γ)(γ α) + (γ α) (α β))
= (α β + β γ + γ α)2 −2 αβγ (β + γ + α) = (b)2 = −2(−c)(−a) = b2 − 2ca
∑3 = α2 β2 γ2 = (α β γ)2 = (−c)2 = c2
எனவே, தேவையான சமன்பாடு,
x3 − (α2 + β2 + γ2)x2 + (α2 β2 + β2 γ2 + γ2 α2)x − α2 β2 γ2 = 0.
x3 − (a2 −2b)x2 + (b2 − 2ca)x − c2 = 0 ஆகும்.
எடுத்துக்காட்டு 3.7
p என்பது ஒரு மெய்யெண் எனில், 4x2 + 4px + p + 2 = 0 எனும் சமன்பாட்டின் மூலங்களின் தன்மையை p −ன் அடிப்படையில் ஆராய்க.
தீர்வு
பண்புகாட்டி ∆ = (4p)2 − 4(4)(p + 2) = 16(p2 – p − 2) = 16(p + 1)(p − 2) ஆகும்.
எனவே,
−1 < p < 2 எனில், ∆ < 0
p = −1 அல்லது p = 2 எனில், ∆ = 0
–∞ < p < −1 அல்லது 2 < p < ∞ எனில், ∆ > 0
எனவே, கொடுக்கப்பட்டுள்ள பல்லுறுப்புக்கோவைக்கு,
−1 < p < 2 எனில், கலப்பெண் மூலங்களைப் பெற்றிருக்கும்;
p = −1 அல்லது p = 2 எனில், சமமான மெய்யெண் மூலங்களைப் பெற்றிருக்கும் ;
−∞ < p < −1 அல்லது 2 < p < ∞ எனில், வெவ்வேறான மெய்யெண் மூலங்களைப் பெற்றிருக்கும்.