முழுக்களின் பெருக்கல்

முழுக்களின் பெருக்கல்

சூழல் 1

இரமணி, இரவி ஆகிய இருவரும் கூழாங்கற்களைக் குவியலாக வைத்து விளையாடிக் கொண்டிருந்தனர். இரமணி சில கூழாங்கற்களைச் சேர்க்கிறார். இரவி சில கூழாங்கற்களை நீக்குகிறார். முதலில் இரமணி 3 கற்களைச் சேர்க்கிறாள். பின்னர் அவள் மேலும் 3 கற்களைச் சேர்க்கிறாள். இதுபோல மேலும் 2 முறை அவள் சேர்க்கிறாள். மொத்தம் எத்தனை கற்களை அவள் சேர்த்தாள் எனக் கூற முடியுமா? கற்களைச் சேர்ப்பவை என்பது மிகை எண் என்பதால் அதனை இப்படி எழுதலாம் ( +3) + ( +3) + ( +3) + ( +3) = +12 அல்லது 4 × (+3) = 12

எனவே இரமணி சேர்த்த மொத்தக் கூழாங்கற்களின் எண்ணிக்கை 12 ஆகும்.

இரவி ஒவ்வொரு முறையும் 5 கூழாங்கற்களை வெளியே எடுக்கிறார். அதே போல் அவன் 3 முறை செய்தால், கற்களை எடுப்பது குறை எண் என்பதால் அதனை ( −5) + ( −5) + ( −5) = −15 அல்லது ( −5) × 3 = −15. என்று எழுதலாம். எனவே இரவி நீக்கிய மொத்தக் கூழாங்கற்களின் எண்ணிக்கை 15 ஆகும். இதிலிருந்து குறை முழுக்களின் பெருக்கலானது மிகை முழுக்களின் பெருக்கலைப் போலவே தொடர் கூட்டலாகும் என்பதை உணர்கிறோம்.

மேலும் எண்கோடு வரைந்து அதன் மூலம் முழுக்களின் பெருக்கலானது ஒரு தொடர் கூடுதலே என அறியலாம்.

4 × 3 = 12  (3ஐ நான்கு முறைக் கூட்டுக).

(−5) × 3 = −15 ((–5) ஐ மூன்று முறைக் கூட்டுக).

மேலும் ஒரு மிகை முழு (+7) ஐ மற்றொரு மிகை முழு (+8) ஆல் பெருக்கக் கிடைப்பது (+56), ஒரு மிகை முழு என்பது நாம் அறிந்ததே. ஒரு மிகை முழு +7 ஐ ஒரு குறை முழு -5 ஆல் பெருக்கக் கிடைப்பது -35 மற்றும் +5 × −7 = −35. ஆனால், ஒரு குறை முழுவான (-3) ஐ மற்றொரு குறை முழுவான (-5) ஆல் பெருக்கக் கிடைப்பது யாது? கீழ்க்காணும் முறையினை உற்றுநோக்குக.

( −5)×3 = −15

( −5)×2 = −10

(−5)×1 = −5

( −5)×0 = 0

( −5)×(−1) = +5

(−5)× (−2) = +10

( −5)× (−3) = 15

இங்கு,-15 லிருந்து -10,-10 லிருந்து -5,-5 லிருந்து 0 என ஒவ்வொரு படியிலும் எண்ணிக்கை 5 இன் மடங்கில் அதிகரிக்கின்றது. இந்த அமைப்பு முறையில் அடுத்த எண், +5 மட்டுமே, -5 இல்லை . இதே போல் (-5) × (-2) இன் பெருக்கல் தொகை மிகை முழு 10 ஆகும். மேற்கண்ட எடுத்துக்காட்டிலிருந்து நாம் அறிவது இரு குறை முழுக்களைப் பெருக்கக் கிடைப்பது ஓர் மிகை முழு என்பதே.

இவற்றை முயல்க

1. பெருக்கற்பலன் காண்க.

(i) ( −20) × ( −45) = 900

(ii) ( −9) × ( −8) = 72

(iii) ( −30) × 40 × ( −1) = 1200

(iv) ( +50) × 2 × ( −10) = –1000

2. கீழ்க்காணும் அட்டவணையில் நிரல் மற்றும் நிறையில் உள்ள முழுக்களைப் பெருக்கி அட்டவணையை நிரப்புக.

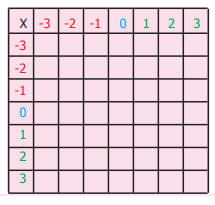
விடை :

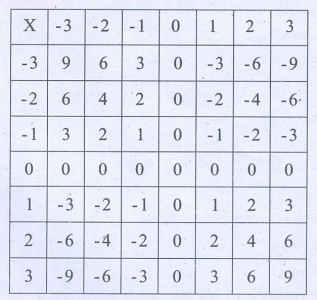
3. கீழ்க்கண்டவற்றில் தவறானது எது?

(i) (-55) × (-22) × (-33)<0 

விடை : –55 × –22 × –33 = – (55 × 22 × 33) < 0 என்பது சரி 

(ii) (-1521) ×2511<0 

விடை : –1521 × 2511 < 0 என்பது சரி

(iii) 2512-1252<0 

விடை :

2512 × 1252= 1260 > 0

எனவே  2512 – 1252 < 0 என்பது சரி

(iv) (+1981) × (+2000)<0

விடை :

+ 1981 × + 2000 = +(1981 × 2000) > 0

எனவே + 1981 × + 2000 < 0 என்பது சரி

சிந்திக்க 

15 × 16 இன் பெருக்குத் தொகையை முழுக்களின் கூட்டலாகவோ அல்லது முழுக்களின் வேறுபாடாகவோ வெளிப்படுத்த முடியுமா?

ஆம், 15 × 16 = +240 என்பதைக் கீழ்க்காணும் நான்கு வழிகளில் கணக்கிட இயலும். 

(i) 15×16 = (10+5)×(10+6) =100+60+50+30 = 240

(ii) 15 ×16 = (20 − 5)× (10 + 6) = 200 +120 + (−50)+ (−20) = 240

(iii) 15 ×16 = (10 + 5)× (20 − 4) = 200 + (−40)+100 + (−20) = 240

(iv) 15 ×16 = (20 − 5)× (20 − 4) = 400 + (−80)+ (−100)+ 20 = 240

மேற்கண்ட அமைப்பில் இருந்து, இரு மிகை முழுக்கள், இரு குறை முழுக்கள் மற்றும் ஒரு மிகை முழுவுடன் ஒரு குறை முழு ஆகியவற்றின் பெருக்கற்பலனைக் கண்டறியலாம்.

எடுத்துக்காட்டு 1.17 

மதிப்பைக் காண்க: 

(i) (–35) × (–11)

(ii) 96 × (–20)

(iii) (–5) × 12

(iv) 15×5

(v) 999 × 0

தீர்வு 

(i) (–35) × (–11) = 385

(ii) 96 × (–20) = – 1920

(iii) (–5) × 12 = –60

(iv) 15 × 5 = 75

(v) 999 x 0 = 0

எடுத்துக்காட்டு 1.18 

ஒரு பழ வியாபாரி கிலோவுக்கு ₹ 15 லாபம் வீதம் 5 கிலோ மாம்பழங்களை விற்றார். பிறகு கிலோவுக்கு ₹ 30 நட்டம் வீதம் 3 கிலோ ஆப்பிள்களை விற்றார் எனில் அவருடைய நிகர லாபம் அல்லது நட்டம் எவ்வளவு? 

தீர்வு

1 கி.கி மாம்பழம் விற்றதில் கிடைக்கும் லாபம் =  ₹ 15 

5 கி.கி மாம்பழம் விற்றதில் கிடைக்கும் லாபம் =  ₹ 15 × 5 

=  ₹ 75

1 கி.கி ஆப்பிள் விற்றதில் கிடைக்கும் நட்டம் =  ₹ 30

3 கி.கி ஆப்பிள் விற்றதில் கிடைக்கும் நட்டம் = 30 × 3 

=  ₹  90 

லாபத்தை விட நட்டம் அதிகம் என்பதால் மொத்த நட்டம் = ₹ 90 - ₹ 75

=  ₹ 15

எடுத்துக்காட்டு 1.19

ஓர் இணைய மையத்தில் மணிக்கு ₹ 15 என இணையத்தைப் பயன்படுத்துவதற்கான கட்டணம் வசூலிக்கப்படுகிறது. நிலா, தினமும் 2 மணி நேரம் வீதம் ஒரு வாரத்தில் 5 நாள்களுக்குப் பயன்படுத்தினால் எவ்வளவு கட்டணம் செலுத்த வேண்டும்? 

தீர்வு

ஒரு நாளைக்கு இணைய மையத்தில் செலவிடும் நேரம் = 2 மணி நேரங்கள் 

5 நாள்களுக்கு இணைய மையத்தில் செலவிடும் நேரம் = 5 × 2

= 10 மணி நேரங்கள் 

ஒரு மணி நேரத்திற்கு உலவுதல் கட்டணம் =  ₹  15

எனவே 10 மணிநேரத்திற்கு உலவுதல் கட்டணம் = 15 × 10 

நிலா 10 மணி நேரம் இணையத்தைப் பயன்படுத்துவதற்கான மொத்தக் கட்டணம் ₹ 150 ஆகும்.