முழுக்களின் கழித்தல்

முழுக்களின் கழித்தல்

முழுக்களின் கழித்தல் என்பது மற்றொரு அடிப்படைச் செயல் ஆகும். நாம் ஏற்கனவே பயன்படுத்திய எண்கோட்டுச் செயல்பாட்டைக் கொண்டே முழுக்களின் கழித்தலைப் பற்றிக் காண்போம். கழிக்கும்பொழுது எண்கோட்டில் குறை முழுத் திசை நோக்கித் திரும்ப வேண்டும்.

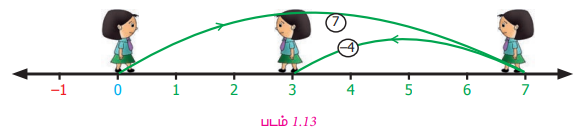
 (+7) லிருந்து (+4) ஐக் கழிக்க

பூச்சியத்தைத் தொடக்க நிலையாகக் கொண்டு மிகைமுழுத் திசை நோக்கி நிற்க. (+7) ஐக் குறிப்பதற்கு 7 அலகுகள் முன்னோக்கி நகர வேண்டும். கழித்தலைக் குறிப்பதற்குக் குறைமுழுத் திசையை நோக்கித் திரும்ப வேண்டும். பின்னர் (+4) ஐக் குறிக்க 7லிருந்து 4 அலகுகள் முன்னோக்கி நகர வேண்டும். தற்போதைய நிலை +3.

எனவே , (+7) - (+4) = +3.

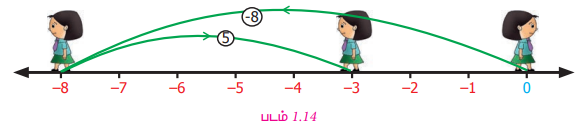
(-8) - (-5) ஐக் கண்டு பிடிப்போம். 

பூச்சியத்தைத் தொடக்க நிலையாகக் கொண்டு மிகைமுழுத் திசை நோக்கி நிற்க. -8 ஐக் குறிப்பதற்கு 8 அலகுகள் பின்னோக்கி நகர வேண்டும். தற்போது அடைந்த நிலை -8. கழித்தலைக் குறிப்பதற்குக் குறைமுழுத் திசை நோக்கித் திரும்ப வேண்டும்.

(-5) ஐக் குறிப்பதற்கு 5 அலகுகள் பின்னோக்கி நகர வேண்டும். தற்போது அடைந்த நிலை -3. அதாவது (-8) - (-5) = (-3).

நாம் கழித்தலை மற்றொரு முறையில் கற்போம். பின்வரும் அமைப்பை உற்றுநோக்குக.

7 - 2 = 5; 7 – 1 = 6; 7 – 0 = 7

இவற்றையே குறை முழுக்களுக்கு விரிவுபடுத்தும்போது என்ன நிகழும்?

7−(−1)= 8; 7 −(−2) = 9; 7 −(−3) = 10

மேலும் ஓர் அமைப்பு முறையைக் காண்போம்.

20−2 =18; 20−1=19; 20−0 = 20; 20−(−1)= 21; 20 −(−2) = 22

மேற்கண்ட அமைப்பு முறையில் 7 மற்றும் 20 என்ற எண்களிலிருந்து அடுத்தடுத்த குறை முழுக்களைக் கழிக்கும்பொழுது அதன் வேறுபாடும் அடுத்தடுத்து அதிகரிக்கிறது என்பதனை நாம் அறிகிறோம்.

குறை முழுக்களைக் கழிக்கும்பொழுது கிடைக்கும் வேறுபாடானது அதிகரிக்கிறது என்பதனை இதிலிருந்து நாம் அறியலாம். எடுத்துக்காட்டாக 7-(-2) =9. எனவே -2 ஐக் கழிப்பது என்பது 2 ஐக் கூட்டுவதற்குச் சமம்.

அதாவது -2 இன் கூட்டல் நேர்மாறு +2, அதாவது 7+2 = 9.

இதிலிருந்து முழுக்களின் கழித்தலில் குறை முழுவைக் கழிப்பதற்கு மாற்றாக அதனுடைய கூட்டல் நேர்மாறைக் கூட்டலாம் என்று அறிகிறோம்.

எடுத்துக்காட்டாக 7 லிருந்து (-5) ஐக் கழிக்க. 7 - (-5) 

(-5) ஐக் கழிப்பதற்கு மாற்றாக (-5) இன் கூட்டல் நேர்மாறான 5ஐ       7உடன் கூட்ட வேண்டும். 

ஆகவே,  7-(-5) = 12.

இவற்றை முயல்க 

1. எண்கோட்டைப் பயன்படுத்தித் தீர்க்க:

(i) (-4) - (+3);

(–4) – (+3) = –7

(ii)  (-4) - (-3) 

(–4) – (–3) = –4 + 3 = –1

2. கீழ்க்கண்டவற்றின் மதிப்புகளைக் கண்டறிந்து அவற்றின் விடைகளை ஒப்பிடுக.

(i) (-6)-(-2) மற்றும் (-6)+2 

(–6) – (–2), –6 + 2 = –4

–6 + 2 = –4

(–6) – (–2) = (–6) + 2

சமமானவை 

(ii) 35-(-7) மற்றும் 35 + 7

35 – (–7) = 35 + 7 = 42

35 + 7 = 42

35 – (–7) = 35 + 7

சமமானவை 

(i) -10 – 8 _____ -10 +8

(ii) (-20) + 10 _____ (-20) - (-10) 

(iii) (-70) - (-50) _____ (-70) -50 

(iv) 100 - (+100) ______ 100 - (-100) 

(v) -50-30 _____  -100 + 20

(i) – 10 – 8 < – 10 + 8

(ii) (–20) + 10  = –20 – (–10)

(iii) (–70) – (–50)  > (–70) – 50

(iv) 100 – (+100)  < 100– (–100)

(v) –50 – 30 = –100 + 20

குறிப்பு 

ஒவ்வொரு கழித்தல் செயல்பாடும், ஒரு கூட்டல் செயல்பாட்டை உள்ளடக்கியிருக்கும். எடுத்துக்காட்டாக, 8 – 5 = 3 என்ற கழித்தல் செயல்பாட்டிலிருந்து 3 + 5 = 8 என்ற கூட்டல் செயல்பாட்டைப் பெறலாம். அதே போன்று (-8) - (-5)= - 3 என்ற கழித்தல் செயல்பாட்டை (-8) = (-3) + (-5) என எழுதலாம்.

எடுத்துக்காட்டு 1.10 

எண்கோட்டைப் பயன்படுத்திக் கழிக்க

(i) –3 – (–2) 

(ii) +6 – (–5)

தீர்வு 

(i) –3 – (–2)

எண்கோட்டைப் பயன்படுத்தி -3 லிருந்து -2 ஐக் கழிப்பதற்கு,

எனவே, –3 – (–2) = –3 + 2 = –1

(ii) +6 – (–5)

எண்கோட்டைப் பயன்படுத்தி 6 லிருந்து -5 ஐக் கழிப்பதற்கு

எனவே, +6 - (-5) = +6 + 5 = 11. 

நாம் கூட்டல் நேர்மாறைப் பயன்படுத்தி முழுக்களின் கழித்தல் செயல்பாட்டைப் பற்றி பார்க்கலாம்.

எடுத்துக்காட்டு 1.11

(i) 70 லிருந்து (-40) ஐக் கழிக்க

(ii) (-20) லிருந்து (-12) ஐக் கழிக்க

தீர்வு 

(i)  70 - (-40)

 = 70 + [(-40) இன் கூட்டல் நேர்மாறு] 

 = 70 + 40

 = 110.

(ii)  (-20) - (-12) 

= (-20) + [(-12) இன் கூட்டல் நேர்மாறு] 

= (-20) + 12 

= - 8 

எடுத்துக்காட்டு 1.12

மதிப்பைக் காண்க : 

(i) ( −11) − ( −33) 

(ii) (−90) − ( −50) 

தீர்வு 

(i) ( −11) − ( −33)

= (−11)+ (+33)

= 22

(ii) (−90) − ( −50)

= −90 −(−50)

= −90+50

= −40

எடுத்துக்காட்டு 1.13

சித்ரா என்பவர் தன்னிடம் ₹ 150 வைத்துள்ளார். அவர் ₹ 225 மதிப்புள்ள ஒரு கைப்பையை வாங்க நினைத்தால் அவர் தோழியிடம் கடன் பெற வேண்டிய தொகை எவ்வளவு?

தீர்வு

சித்ராவிடம் இருப்புத் தொகை = ₹ 150

கைப்பையின் மதிப்பு = ₹ 225 

கடன் பெறவேண்டிய தொகை = ₹ 225 - ₹ 150

= 75 

எடுத்துக்காட்டு 1.14

செழியன் என்பவர் அவருடைய வங்கிக் கணக்கில் இருந்து ₹ 1079 மதிப்புள்ள பொருள்களை வாங்குகிறார். அதற்கு முன்பு அவருடைய கணக்கில் ₹ 5000 இருந்திருந்தால், தற்போது அவருடைய கணக்கில் எவ்வளவு பணம் இருக்கும்? 

தீர்வு

ஆரம்ப இருப்பு = ₹ 5000 

செலவிட்ட தொகை = ₹ 1079 (-)

மீதமுள்ள இருப்பு = ₹ 3921 

எடுத்துக்காட்டு 1.15

வெள்ளிக்கிழமை ஸ்ரீநகரின் வெப்பநிலை -3°C எனப் பதிவாகியுள்ளது. மறுநாள் வெப்பநிலை 1°C குறைந்தால், அன்றைய வெப்பநிலையைக் காண்க.

தீர்வு 

வெள்ளிக்கிழமை ஸ்ரீநகரின் வெப்பநிலை -3°C. மறுநாள் வெப்பநிலை 1°C குறைந்தது. 

மறுநாளின் வெப்பநிலை = −3°C – 1°C = −4°C.

எடுத்துக்காட்டு 1.16

ஒரு நீர்மூழ்கிக் கப்பல் கடல் மட்டத்தைவிட 300 அடிகள் கீழே உள்ளது. பிறகு, கப்பல் 175 அடிகள் மேல் நோக்கிச் செல்கிறது எனில், கப்பலின் தற்போதைய நிலை என்ன? 

தீர்வு 

நீர்மூழ்கிக் கப்பலின் ஆரம்ப நிலை = கடல் மட்டத்திற்கு 300 அடிகள்கீழ்

= - 300 அடிகள் 

நீர்மூழ்கிக் கப்பல் மேல் நோக்கிச் சென்ற தூரம் = 175 அடிகள்

= + 175 அடிகள்

நீர்மூழ்கிக் கப்பலின் தற்போதைய நிலை = (-300) + (+175)

= -125

அதாவது, நீர்மூழ்கிக் கப்பல் கடல் மட்டத்திலிருந்து 125 அடிகள் கீழே உள்ளது.