கூட்டல் பண்புகள்

கூட்டல் பண்புகள்

முழு எண்களின் தொகுப்புக் கூட்டலைப் பொறுத்து அடைவுப் பண்பினை நிறைவு செய்கிறது என்பதனை நாம் ஆறாம் வகுப்பில் பயின்றுள்ளோம். இரு முழு எண்களின் கூடுதல் எப்போதும் ஓர் முழு எண் ஆகும். இப்பண்பு முழுக்களின் தொகுப்பிற்குப் பொருந்துமா?

இரு முழுக்களின் கூடுதல் ஓர் முழு எண்ணா என்பதனைக் கீழ்க்கண்ட அட்டவணையைக் கொண்டு சோதிக்கவும். 

மேற்காண்பனவற்றில் இருந்து இரு முழுக்களின் கூடுதல் ஓர் முழு என அறிகிறோம். இதிலிருந்து முழுக்களின் தொகுப்பு அடைவுப் பண்பினை நிறைவு செய்கிறது என்பதை அறிகிறோம். இப்பண்பினை முழுக்கள் கூட்டலைப் பொறுத்து அடைவுப் பண்பினைப் பெற்றுள்ளது என்கிறோம்.

ஆகையால், பொதுவாக a, b என்பன ஏதேனும் இரண்டு முழுக்கள் எனில் a+b ஒரு முழு ஆகும்.

மேலும் ஒரு பண்பு பற்றி இங்குக் காண்போம். இரு முழுக்களின் வரிசையை மாற்றிக் கூட்டினாலும் அதன் கூட்டல் பலன் மாறாது. எடுத்துக்காட்டாக, 12 + ( −13) மற்றும் ( −13) + (12) ன் கூட்டல் பலன் சமம். மேலும் (-7) + (-5) = -12, (-5) + (-7) = -12

இப்பண்பினை முழுக்களுடைய கூட்டலின் பரிமாற்றுப் பண்பு என்கிறோம். 

ஆகையால், பொதுவாக a, b என்ற ஏதேனும் இரு முழுக்களுக்கு a, b; a+b = b+a.

மூன்று முழுக்களைக் கூட்டினால் அதன் கூட்டல் பலன் எப்படி இருக்கும்? எடுத்துக்காட்டாக, (-7) + (-2) + (-9) ஐ வரிசை மாற்றிக் கூட்டும்பொழுது அதன் கூட்டல் பலன் சமமாக இருக்குமா?

[(-7) + (-2) + (-9) மற்றும் (-7) + [(-2) + (-9)]. என்றவாறு வரிசை மாற்றி முழுக்களைக் கூட்டிச் சோதிக்க

[(-7)+(-2)]+ (-9). இன் மதிப்பைக் கண்டறிதல்

[(-7)+(-2)]+ (-9) = (-9) + (-9) = -9-9= -18 

[(-7)+ (-2)]+(-9) என்பதனை எண்கோட்டில் குறிக்க.

[ (−7)+ (−2) ] + (−9) = (−18) 

 (–7) + [(–2) + (–9)] இன் மதிப்பைக் கண்டறிதல் 

(–7) + [(–2) + (–9)] = (–7) + (–11) = –7 – 11 = –18

(–7) + [(–2) + (–9)] என்பதனை எண் கோட்டில் குறிக்க.

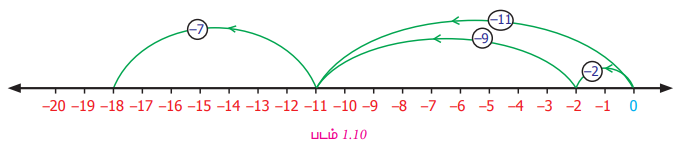
(−7)+ [(−2)  + (−9)] = (−18)

இரு முறைகளிலும் நமக்குக் கிடைக்கும் தீர்வு -18 லிருந்து எண்களின் வரிசையை மாற்றிக் கூட்டினாலும் அதன் மதிப்பு மாறாது என்று அறிகிறோம். இப்பண்பினை முழுக்களின் கூட்டலில் சேர்ப்புப் பண்பு என்கிறோம்.

ஆகையால், பொதுவாக a, b, c என்ற ஏதேனும் மூன்று முழுக்கள் எனில், a+(b+c) = (a+b)+c.

மிகை எண்கள், குறை எண்கள், பூச்சியம் ஆகியவற்றின் தொகுப்பே முழுக்கள் ஆகும். இங்குப் பூச்சியம் ஒரு மிகை முழுவும் அல்ல, ஒரு குறை முழுவும் அல்ல என்பது கவனிக்கத் தக்கது. ஏதேனும் ஒரு முழுவைப் பூச்சியத்துடன் கூட்டும்பொழுது நிகழ்வது என்ன?

எடுத்துக்காட்டாக, 7+0=7, (–3)+0 = (–3), (–27)+0 = (–27), 

 (–79)+0 = (–79), 0+(–69) = (–69), 0+(–85) = (–85).

பூச்சியத்துடன் எந்த முழுவைக் கூட்டினாலும், அதே முழுவை விடையாகப் பெறலாம். இதுவே பூச்சியத்தின் சிறப்பியல்பு ஆகும். பூச்சியம் என்பது முழுக்களின் கூட்டலைப் பொறுத்து சமனி உறுப்பு அல்லது கூட்டல் சமனி எனப்படுகிறது.

ஆகையால், பொதுவாக ஏதேனும் ஒரு முழு a இக்கு, a+0 = a = 0+a

முழுக்களின் கூட்டல் சமனி, பூச்சியமானது எண்கோட்டை மிகை முழுக்கள் குறை முழுக்கள் எனப் பிரிக்கிறது. "0"வின் இரு புறங்களிலும் சமதூரத்தில் உள்ள எண்கள் ஒன்றுக்கொன்று எதிர்மறையாக உள்ளன. அதாவது +1 மற்றும் -1, +5 மற்றும் -5,-15 மற்றும் +15. இவ்வெண்கள் அனைத்தும் எதிரெதிர்த் திசையில் அமைந்துள்ளன. இவ்வாறாக உள்ள எதிர்மறை எண்களைக் கூட்டும்பொழுது எப்போதும் நமக்குப் பூச்சியம் கிடைக்கிறது.

எடுத்துக்காட்டாக, ( −15) +15 = 0 , 21 + ( −21) = 0. முழுக்களின் இப்பண்பு "கூட்டல் எதிர்மறை" என்று அழைக்கப்படுகிறது. (-15) இன் கூட்டல் எதிர்மறை +15. ஏனெனில் இவ்விரு எண்களின் கூடுதல் பூச்சியம். இவ்வாறாக, 21 இன் கூட்டல் எதிர்மறை -21. ஒரு சோடி எதிரெதிர் முழுக்களைக் கூட்டல் எதிர்மறை முழுக்கள் என்கிறோம்.

ஆகையால், ஏதேனும் ஒரு முழு a இக்கு -a என்பது கூட்டல் எதிர்மறை ஆகும். 

a+ (-a) = 0 = (-a)+a

இவற்றை முயல்க 

1. கோடிட்ட இடங்களை நிரப்புக:

(i) 20 + (-11) = (–11) +20

(ii) (-5)+(-8) = (-8)+ (–5)

(iii) (-3)+12= 12 +(-3) 

2. சரியா, தவறா எனக் கூறுக

(i) ( −11) + ( −8) = ( −8) + ( −11) (சரி)

(ii) −7 + 2 = 2 + ( −7) (சரி)

(iii) ( −33) + 8 = 8 + ( −33) (சரி)

3. கீழ்க்காண்பனவற்றைச் சோதிக்க:

(i) [( −2) + ( −9)] + 6 = ( −2) + [(−9) + 6] 

[(-2) + (-9)] +6 = (–11) + 6 = (–5)

மேலும் (-2) + [(-9) +6] = (-2) + (-3) = -5

இரு புறங்களின் மதிப்பும் சமம், எனவே

[(-2) + (-9)] +6 = (-2) + [(-9) + 6]

(ii) [7 + ( −8)] + ( −5) = 7 + [(−8) + ( −5)]

முதலில் [7+(–8)] + (–5) = (-1) + (-5) = -6

மேலும் 7 + [(-8) + (-5)] = 7 + (-13) = 7-13 = -6

இரு புறங்களின் மதிப்பும் சமம்

7 + [–8 + –5] = 7 + [(-8) + (-5)

(iii) [(−11)+ 5] + (−14) = (−11)+ [5 + (−14)]

மேலும் [(-11) +5] + (-14) = (-6) + (-14) = (-20)

மேலும் (-11) +[5 + (-14) ] = (-11) + (-9) = -20

இரு புறங்களின் மதிப்பும் சமம்

எனவே [(-11) + 5] + (-14) = (-11) + [5+ (-14)]

(iv) ( −5) + [( −32) + ( −2)] = [( −5) + ( −32)] + ( −2)

 (–5) + [(–32) + (–2)] = (-5) + (-34) = -39

மேலும் [(-5) + (-32)] + (-2) = (-37) + (-2) = -39

4. விடுபட்ட முழுக்களைக் கண்டுபிடிக்க.

(i) 0 + (–95) = –95

(ii) −611 + 0 = −611

(iii) –79 + 0 = –79

(iv) 0 + ( −140) = –140

5. கீழுள்ளவற்றைப் பூர்த்தி செய்க:

(i) −603 + 603 = 0

(ii) 9847 + ( −9847) = 0

(iii) 1652 + (–1652) = 0

(iv) −777 + 777 = 0

(v) –5281 + 5281 = 0

எடுத்துக்காட்டு 1.7 

(i) 120 + 51 மற்றும் 51 + 120 ஆகிய இரண்டும் சமமானவையா?

(ii) (-5)+[(-4)+(-3)] மற்றும் [(-5)+(-4)]+(-3) ஆகிய இரண்டும் சமமானவையா? 

தீர்வு 

(i) 120 + 51 = 171 ; 51 + 120 = 171 என எழுதலாம்.

மேலும், இவ்விரு நிகழ்வுகளிலும் நமக்குக் கிடைக்கும் விடை சமம். முழுக்களை வரிசை மாற்றிக் கூட்ட இயலும். முழுக்களின் கூட்டல் பரிமாற்றுப் பண்பை நிறைவு செய்கிறது. 

(ii) ( −5) + [( −4) + ( −3)]  மற்றும் [( −5) + ( −4)] + ( −3) 

(–5) +[(–4) +(–3)], இல் முதலில் (–4) மற்றும் (–3) கூட்டப்பட்டுள்ளது.  பின்னர் இதனுடைய விடையுடன் (-5) ஐக் கூட்டுகிறோம்.

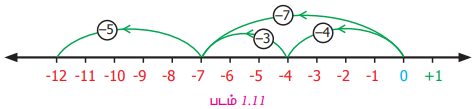
(–5) +[(–4) +(–3)] = –12 

[(-5)+(-4)]+(-3) இல், முதலில் (-5) மற்றும் (-4) கூட்டப்பட்டு அதன் விடையுடன் (-3) ஐக் கூட்டுகிறோம்.

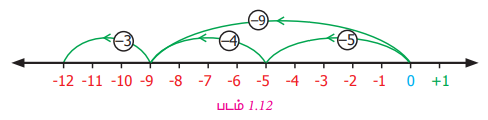
[(-5) +(-4)] + (-3) = -12 

இவ்விரு வகையிலும், -12 என்ற விடை கிடைக்கிறது. 

ஆகவே, (-5)+[(-4)+(-3)]=[(-5)+(-4)]+(-3) 

முழுக்களின் கூட்டலானது சேர்ப்புப் பண்பை நிறைவு செய்கிறது.

எடுத்துக்காட்டு 1.8 

விடுபட்ட முழுக்களைக் காண்க

(i) 0 + ( −2345) = ______

 (ii) 23479 + _____ = 0

தீர்வு  

(i) 0+(-2345)=-2345

(ii) 23479+(-23479)= 0 

ஆகவே, 23479 இன் கூட்டல் எதிர்மறை -23479 ஆகும்.

எடுத்துக்காட்டு 1.9 

கீழ்க்கண்ட சமன்பாடுகளிலுள்ள பண்புகளைக் குறிப்பிடுக. 

(i) (−45)+ (−12) = −57

(ii) (−15)+ 7 = (7)+ (−15)

(iii) −10+3= −7

(iv) (−7)+ (−5) = (−5)+ (−7)

(v) (−7)+ [(−4)+ (−3)] = [(−7)+ (−4)] + (−3)

(vi) 0 + (−7245) = −7245

தீர்வு 

(i) அடைவுப் பண்பு 

(ii) பரிமாற்றுப் பண்பு 

(iii) அடைவுப் பண்பு 

(iv) பரிமாற்றுப் பண்பு 

(v) சேர்ப்புப் பண்பு 

(vi) கூட்டல் சமனி