சாய்வினை வகையிடல் மூலம் காணுதல் (Derivative as slope)

வகையிடலின் பொருள் (Meaning of Derivatives) 

சாய்வினை வகையிடல் மூலம் காணுதல் (Derivative as slope)

ஒரு கோட்டின் சாய்வு அல்லது சரிவு : படத்தில் உள்ளது போல் Ɩ என்பது செங்குத்தற்ற கோடு என்க. கொடுக்கப்பட்ட Ɩ கோட்டில் துவக்கப் புள்ளியாகக் கொண்டு ஏதேனும் ஒரு அளவு நீளம் கொண்ட முடிவுறு கிடைமட்ட கோட்டுத் துண்டும் இக்கிடைமட்ட கோட்டுத் துண்டின் முடிவுப் புள்ளியினை துவக்கப்புள்ளியாகக் கொண்டு கொடுக்கப்பட்ட கோட்டினைத் தொடுமாறு வரையப்படுகிறது. செங்குத்து நீளமும் கிடைமட்ட நீளமும் விகிதாச்சாரப்படி மாறிலியாக இருப்பதைக் கவனிக்கலாம். இந்த விகிதமேƖ கோட்டின் சாய்வு எனப்படும். இது m எனக் குறிப்பிடப்படுகிறது.

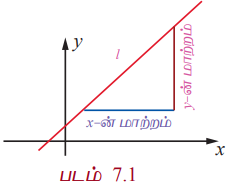
ஒரு கோட்டின் ஏறுதல் அல்லது இறங்குதல் தன்மையை அளவிட சாய்வினைப் பயன்படுத்தலாம். கோடு ஏறுதல் அல்லது இறங்குதல் முறையே m > 0 அல்லது m < 0 பொறுத்து அமையும். m = 0 எனில், y ஆனது மாறுவதில்லை. கோட்டின் சாய்வினை m என்று குறிப்பிட்டால் XY தளத்தில் y = mx + c ஒரு நேர்க்கோட்டைக் குறிக்கிறது என்பதை நினைவுகூர்க.

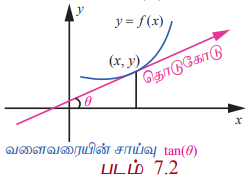
ஒரு வளைவரையின் சாய்வு அல்லது சரிவு : y = f (x) என்பது கொடுக்கப்பட்ட வளைவரை என்க. (x, f (x)) மற்றும் (x+h, f (x+ h)) என்ற இரு வெவ்வேறு புள்ளிகளை இணைக்கும் ஒரு கோட்டின் சாய்வு

f (x+h) - f (x) / h (நியூட்டன் ஈவு). -----------.(1)

h → 0 எனும்போது எல்லையானது 

lim h → 0 f (x+h) - f (x) / h = f’(x), (நியூட்டனின் ஈவின் எல்லை ) ------------.(2)

என்பது (x,y) அல்லது (x, f (x)) என்ற புள்ளியில் வளைவரையின் சாய்வாகும். 

குறிப்புரை

y = f (x) என்ற வளைவரையில் (x,y) எனும் புள்ளியைப் பொறுத்து ஏற்படும் வளைவரைக்கான தொடுகோட்டின் தொடுகோணம் θ எனில் (x,y) புள்ளியில் வளைவரையின் சாய்வு f'(x) = tan θ ஆகும். இங்கு θ ஆனது, X -அச்சிலிருந்து கடிகார திசைக்கு எதிர்திசையில் அளக்கப்படுகிறது. f'(x) என்பதை dy / dx எனவும் குறிக்கலாம். மேலும் dy/dx ஆனது கணநேர மாறுபாட்டு வீதத்தைக் குறிக்கிறது. நியூட்டனின் ஈவானது கொடுக்கப்பட்ட இடைவெளியில் சராசரி மாறுபாட்டு வீதத்தைக் குறிக்கிறது.

எடுத்துக்காட்டு 7.1

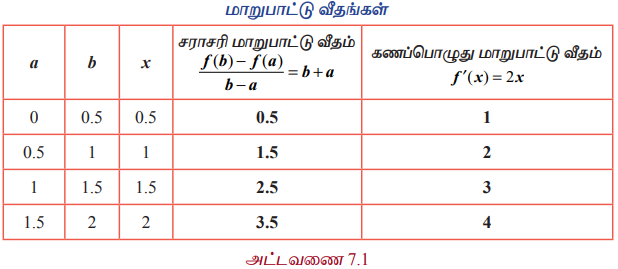
f(x) = x2, x E [0, 2] எனும் சார்பிற்கு [0, 0.5], [0.5,1],[1,1.5],[1.5,2] என்ற உள் இடைவெளிகளில் சராசரி மாறுபாட்டு வீதத்தையும் மற்றும் x = 0.5,1,1.5,2 புள்ளிகளில் ஏற்படும் கணப்பொழுது மாறுபாட்டு வீதங்களையும் காண்க.

தீர்வு 

[a,b] என்ற இடைவெளியில் சராசரி மாறுபாட்டு வீதம் f(b) – f(a) / b –a ஆகும். அதேசமயத்தில் x புள்ளியில் கணப்பொழுது மாறுபாட்டு வீதம் கொடுக்கப்பட்ட சார்பிற்கு f’(x) ஆகும். அவை முறையே, b+a மற்றும் 2x ஆகும்.

மாறுபாட்டு வீதங்கள்