வகை நுண்கணிதத்தின் பயன்பாடுகள் | கணிதவியல் - இரண்டாம் வகைக்கெழுவின் பயன்பாடுகள்(Applications of Second Derivative) | 12th Maths : UNIT 7 : Applications of Differential Calculus
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 7 : வகை நுண்கணிதத்தின் பயன்பாடுகள்
இரண்டாம் வகைக்கெழுவின் பயன்பாடுகள்(Applications of Second Derivative)
இரண்டாம் வகைக்கெழுவின் பயன்பாடுகள்(Applications of Second Derivative)
இரண்டாம் வகைக் கெழுவானது ஒரு சார்பின் குழிவு, குவிவு, வளைவு மாற்றப் புள்ளி மற்றும் இடம் சார்ந்த அறுதி மதிப்புகளை தீர்மானிக்க பயன்படுகின்றது.
குழிவு, குவிவு மற்றும் வளைவு மாற்றப் புள்ளி (Concavity, Convexity, and Points of Inflection)
ஒரு வளைவரைக்கு ஒரு புள்ளியில் வரையப்படும் தொடுகோடு வளைவரைக்கு மேற்புறமாக அமைந்தால் அப்புள்ளியில் வளைவரை கீழ்நோக்கி குழிவு (மேல் நோக்கி குவிவு) என்கிறோம். வளைவரைக்கு ஒரு புள்ளியில் வரையப்படும் தொடுகோடு வளைவரைக்கு கீழ்புறமாக அமைந்தால் அப்புள்ளியில் வளைவரை மேல்நோக்கி குழிவு (கீழ்நோக்கி குவிவு) என்கிறோம். இதனை அருகில் உள்ள வரைபடத்தின் வாயிலாக எளிதில் அறியலாம்.
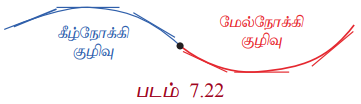
வரையறை 7.8
f(x) என்ற சார்பிற்கு I = (a,b) என்ற திறந்த இடைவெளியில் இரண்டாம் வகைக்கெழு காணத்தக்கது என்க. அப்பொழுது f (x) ஆனது கீழ்க்கண்டவாறு வகைப்படுத்தப்படுகிறது.
(i) f'(x) ஆனது திறந்த இடைவெளி I-ல் திட்டமாக ஏறும் எனில், f (x) ஆனது I-ல் மேல்நோக்கி குழிவு ஆகும்.
(ii) f'(x) ஆனது திறந்த இடைவெளி I-ல் திட்டமாக இறங்கும் எனில், f (x) ஆனது I-ல் கீழ்நோக்கி குழிவு ஆகும்..
பகுப்பாய்வின்படி, y = f (x) என்ற வகையிடத்தக்க வளைவரையின் குழிவுத் தன்மை கீழ்க்காணும் முடிவில் விளக்கப்பட்டுள்ளது.
தேற்றம் 7.11 (குழிவுத் தன்மை சோதனை)
(i) திறந்த இடைவெளி I -ல் f"(x) > 0 எனில், I -ல் f (x) மேல்நோக்கி குழிவு ஆகும்.
(ii) திறந்த இடைவெளி I -ல் f"(x) < 0 எனில், I -ல் f (x) கீழ்நோக்கி குழிவு ஆகும்.
குறிப்புரை
(1) [a,b]-ல் மேல்நோக்கி குவிவு வளைவரையின் எந்த ஒரு இடஞ்சார்ந்த பெருமமும் மீப்பெருபெருமம் ஆகும்.
(2) [a,b]-ல் கீழ்நோக்கி குவிவு வளைவரையின் எந்த ஒரு இடஞ்சார்ந்த சிறுமமும் மீச்சிறுசிறுமம் ஆகும்.
(3) எந்த ஒரு வளைவரைக்கும் ஒரே ஒரு மீப்பெரு பெருமம் (மற்றும் ஒரே ஒரு மீச்சிறு சிறுமம்)மட்டுமே உண்டு. ஆனால் ஒன்றிற்கு மேற்பட்ட இடஞ்சார்ந்த பெருமம் அல்லது இடஞ்சார்ந்தசிறுமம் இருக்கலாம்.
வளைவு மாற்றப்புள்ளி
வரையறை 7.9
ஒருசார்பின் வளைவரையானது எப்புள்ளிகளில் “மேல்நோக்கி குழிவில் இருந்து கீழ்நோக்கி குழிவாகவோ” அல்லது “கீழ்நோக்கி குழிவில் இருந்து மேல்நோக்கி குழிவாகவோ” மாறுகிறதோ அப்புள்ளிகளை f (x) -ன் வளைவு மாற்றப் புள்ளிகள் என அழைக்கிறோம்.
தேற்றம் 7.12 (வளைவு மாற்றப்புள்ளி சோதனை)
(i) f"(c) காணத்தக்கது மற்றும் f"(c)-ன் குறி ஆனது x = c-ஐ கடக்கும்போது மாறுகிறது, எனில் (c, f (c)) ஆனது f -ன் வளைவு மாற்றப் புள்ளி ஆகும்.
(ii) வளைவு மாற்றப்புள்ளி C-யில் f"(c) காணத்தக்கது எனில், f"(c) = 0 ஆகும்.
குறிப்புரை
y = f (x) என்ற வளைவரையின் வளைவு மாற்றப் புள்ளிகளை காண்பதற்கு f’’(x) ஆனது எப்புள்ளிகளில் அதன் குறியை மாற்றுகிறது என்பதை அறிவது அவசியமானதாகும். 'வழவழப்பான வளைவரைகளில் (கூர்முனைகள் அற்ற) கீழ்க்காணும் ஏதேனும் ஒன்று நடக்க வாய்ப்பு உள்ளது:
(i) f”(x) = 0 அல்லது
(ii) f"(x) அப்புள்ளியில் காணத்தக்கது அல்ல.
குறிப்புரை
(1) f"(c) காணத்தக்கதாக இல்லாத நிலையிலும், (c, f (c)) வளைவு மாற்றப் புள்ளியாக இருக்கவாய்ப்புள்ளது. உதாரணமாக, f(x) = x1/3 எனும் வளைவரையில் c = 0 .
(2) f"(c) = 0 எனும் நிலையில் (c, f (c)) ஒரு வளைவு மாற்றப் புள்ளியாக இல்லாமலும் இருக்க வாய்ப்புள்ளது. உதாரணமாக, f (x) = x4 எனும் வளைவரையில் c = 0.
(3) ஒரு வளைவு மாற்றப் புள்ளி தேக்க நிலைப் புள்ளியாக இருக்க வேண்டிய அவசியம் இல்லை. உதாரணமாக f (x) = sin x எனில், f'(x) = cos x மற்றும் f"(x) = -sin x மேலும் இதிலிருந்து (π, 0) ஆனது ஒரு வளைவு மாற்றப் புள்ளி. ஆனால் அது f (x) -ன் தேக்க நிலைப்புள்ளி அல்ல.
எடுத்துக்காட்டு 7.57
f(x) = (x-1)3 (x-5),x ∈ℝ என்ற வளைவரையின் குழிவு இடைவெளிகளைக் காண்க மேலும் ஏதேனும் வளைவு மாற்றப்புள்ளிகள் இருப்பின் அவற்றைக் காண்க.
தீர்வு
கொடுக்கப்பட்ட சார்பு 4-ஆம் வரிசை பல்லுறுப்புக் கோவை ஆகும். இப்பொழுது
f'(x) = (x-1)3 +3(x-1)2 (x-5)
= 4(x-1) 2 . (x-4)
f"(x) = 4[(x-1) 2 + 2(x-1) . (x-4)]
= 12(x-1) (x-3)
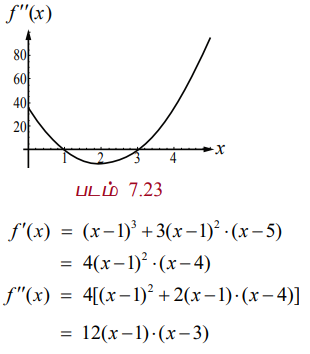
இப்பொழுது, f"(x) = 0 ⇒ x =1, x = 3.
குழிவு இடைவெளிகள் அட்டவணை 7.7-ல் அட்டவணைப்படுத்தப்பட்டுள்ளது.
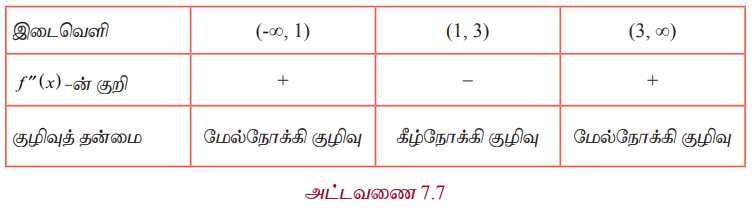
அட்டவணை 7.7
(-∞, 1) மற்றும் (3, ∞) ஆகிய இடைவெளிகளில் வளைவரை மேல்நோக்கி குழிவு ஆகும். (1,3) என்ற இடைவெளியில் வளைவரை கீழ்நோக்கி குழிவு ஆகும்.
f"(x) -ன் குறியானது x = 1 மற்றும் x = 3 ஆகியவற்றைக் கடக்கும்போது மாறுகிறது. எனவே, (1, f (1)) = (1, 0) மற்றும் (3, f (3)) = (3,-16) ஆகியவை y = f (x) என்ற வளைவரையின் வளைவு மாற்றப்புள்ளிகள் ஆகும். குறிமாற்றத்தை அருகில் உள்ள f"(x) -ன் வரைபடத்தின் மூலம் அறியலாம்.
எடுத்துக்காட்டு 7.58
y = 3 + sin x என்ற வளைவரையின் குழிவு இடைவெளிகளைக் காண்க.
தீர்வு
கொடுக்கப்பட்ட சார்பானது 2π பிரிவு இடைவெளி உள்ள சார்பு ஆகும். எனவே இந்த ஒவ்வொரு பிரிவு இடைவெளிகளிலும் தேக்க நிலைப் புள்ளிகள் மற்றும் வளைவு மாற்றப் புள்ளிகள் இருக்கும்.
y = 3 + sin x என்பதில் இருந்து
dy / dx = cos x மற்றும் d2y / dx2 = -sin x
இப்பொழுது, d2y / dx2 = -sin x = 0 ⇒ x = nπ.
(-π,π) என்ற இடைவெளியினை (-π, 0) மற்றும் (0, π) எனும் உள் இடைவெளிகளாக பிரிக்கலாம்.
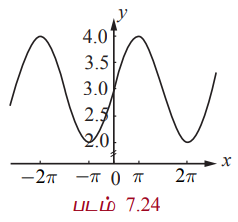
படம் 7.24
(-π, 0) எனும் இடைவெளியில், d2y / dx2 > 0 மேலும் இதிலிருந்து (-π, 0) -ல் சார்பு மேல்நோக்கி குழிவு. (0, π) எனும் இடைவெளியில் d2y / dx2 < 0, மேலும் இதிலிருந்து (0, π) -ல் சார்பு கீழ்நோக்கி குழிவு. ஆகவே, (0,3) என்பது வளைவு மாற்றப்புள்ளி ஆகும் (படம் 7.24ஐ பார்க்க). (n π,(n+1) π ) என்ற பொதுவான இடைவெளிகளைக் கருதும்போது (π ஒரு முழு எண்), இவ்விடைவெளிகளில் குழிவுத்தன்மையை ஆராய வேண்டும். இதனை மேற்கூறியவாறே ஆராய நாம் (nπ,3) ஆகியவை வளைவு மாற்றப்புள்ளிகள் என அறியலாம்.
இரண்டாம் வகைக்கெழு சோதனையை பயன்படுத்தி அறுதி மதிப்புகள்(Extrema using Second Derivative Test)
இரண்டாம் வகைக்கெழு சோதனை: இரண்டாம் வகைக்கெழு சோதனையானது நிலைப்புள்ளிகள், அறுதி மதிப்புகள் மற்றும் குழிவுத்தன்மை போன்றகருத்துகளைதொடர்புபடுத்துவது ஆகும். மேலும் இது நிலைப்புள்ளிகளில் சார்பின் இடஞ்சார்ந்த பெரும அல்லது சிறும மதிப்புகளை ஆராய சிறந்த கருவியாக பயன்படுகிறது.
தேற்றம் 7.13 (இரண்டாம் வகைக்கெழு சோதனை)
c எனும் நிலைப்புள்ளியில் f'(c) = 0 எனவும், c-ன் அண்மையில் f'(x) காணத்தக்கது எனவும், 'மேலும் f"(c) காணத்தக்கது எனவும் கொண்டால்,' f"(c) < 0 எனில் C-யில் f ஆனது இடஞ்சார்ந்த பெருமத்தை அடையும், f"(c) > 0 எனில் C-யில் f ஆனது இடஞ்சார்ந்த சிறுமத்தை அடையும். f''(c) = 0 எனில், இந்த சோதனையில் இடஞ்சார்ந்த அறுதி மதிப்புகளைப் பற்றிய தகவல் இல்லை என்கிறோம்.
எடுத்துக்காட்டு 7.59
f (x) = x4 + 32x என்ற சார்பின் இடஞ்சார்ந்த அறுதி மதிப்புகளைக் காண்க.
தீர்வு
f'(x) = 4x3 + 32 = 0 ⇒ x3 =-8 ⇒ x = -2
மேலும் f"(x) = 12x2
f"(-2) > 0 என்பதால் x = -2-ல் சார்பு இடஞ்சார்ந்த சிறும மதிப்பை அடையும். இந்த இடஞ்சார்ந்த சிறும மதிப்பு f (-2)=-48 ஆகும். எனவே, அறுதிப் புள்ளி (-2,-48)
எடுத்துக்காட்டு 7.60
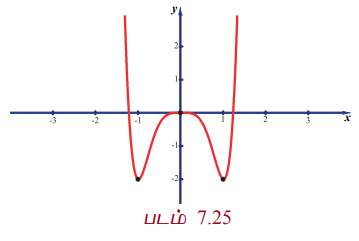
f (x) = 4x6 - 6x4 என்ற சார்பின் இடஞ்சார்ந்த அறுதி மதிப்புகளைக் காண்க.
தீர்வு
x-ஐப் பொருத்து வகையிட,
f' (x) = 24x5 - 24x3
= 24x3 (x2-1)
= 24x3 (x +1)(x-1)
f'(x) = 0 ⇒ x = -1, 0, 1.
ஆகவே நிலை எண்கள் x = -1,0,1 ஆகும்.
இப்பொழுது, f" (x) = 120x4 - 72x2 = 24x2 (5x2 - 3).
⇒ f"(-1) = 48, f" (0) = 0, f" (1) = 48.
f" (-1) மற்றும் f"(1) ஆகியவை மிகை. ஆகவே இரண்டாம் வகைக்கெழு சோதனையின்படி, x = -1,1-ல் இடஞ்சார்ந்த சிறும மதிப்புகள் இருக்கும். ஆனால், x = 0 எனில், f"(0) = 0. x = 0 -ல் இரண்டாம் வகைக்கெழுச் சோதனையானது இடஞ்சார்ந்த அறுதி மதிப்புகளைப் பற்றி எந்த தகவலையும் தருவதில்லை. எனவே, நாம் முதலாம் வகைக்கெழு சோதனையை பயன்படுத்த வேண்டும். ஓரியல்புத்தன்மை இடைவெளிகள் அட்டவணை 7.8-ல் அட்டவணைப்படுத்தப்பட்டுள்ளது.
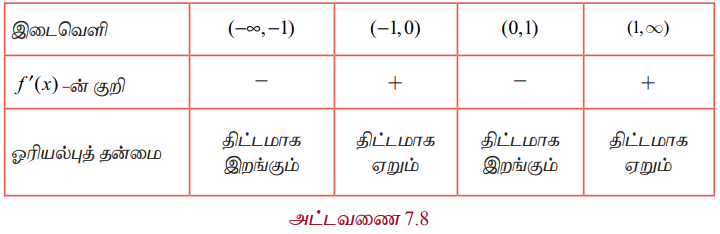
முதலாம் வகைக்கெழு சோதனையின்படி, x =-1-ல் f (x) ஆனது இடஞ்சார்ந்த சிறுமத்தை அடையும், அந்த இடஞ்சார்ந்த சிறுமம் -2 ஆகும். x = 0 -ல் f (x) ஆனது இடஞ்சார்ந்த பெருமத்தை அடையும். அந்த இடஞ்சார்ந்த பெருமம் 0 ஆகும். x = 1 -ல் f (x) ஆனது இடஞ்சார்ந்த சிறும் மதிப்பினை அடையும். அந்த இடஞ்சார்ந்த சிறுமம் - 2 ஆகும்.
குறிப்புரை
இரண்டாம் வகைக்கெழு மறையும் போது, நாம் இடஞ்சார்ந்த அறுதி மதிப்புகளைப் பற்றிய தகவலைப் பெற முடியாது. ஆகவே நாம் இச்சூழல்களில் முதலாம் வகைக்கெழு சோதனையை பயன்படுத்தலாம்!
எடுத்துக்காட்டு 7.61
x2y2 -ன் இடஞ்சார்ந்த பெறும மற்றும் சிறும மதிப்புகளை x + y = 10 என்ற கோட்டின் மீது காண்க.
தீர்வு
கொடுக்கப்பட்ட சார்பை நாம் f (x) = x2 (10-x) 2 என எழுதலாம்.
இப்பொழுது, f (x) = x2(100 - 20x + x2) = x4 - 20x3 + 100x2
எனவே, f'(x) = 4x3 - 60x2 + 200x = 4x(x2 - 15x + 50)
f'(x) = 4x(x2 -15x + 50) = 0 ⇒ x = 0, 5, 10
மேலும். f"(x) = 12x2 - 120x + 200
f(x) -ன் தேக்க நிலை எண்கள் x = 0, 5, 10 ஆகும். இவ்வெண்களில் f"(x)-ன் மதிப்புகள் முறையே 200,-100 மற்றும் 200 ஆகும். x = 0-ல், இடஞ்சார்ந்த சிறும மதிப்பு f (0) = 0 ஆகும். x = 5-ல், இடஞ்சார்ந்த பெரும் மதிப்பு f (5) = 625 ஆகும். x = 10-ல், இடஞ்சார்ந்த சிறும மதிப்பு f (10) = 0 ஆகும்.