வகை நுண்கணிதத்தின் பயன்பாடுகள் | கணிதவியல் - பயன்பாடுகள் (Applications) சராசரி மதிப்புத் தேற்றம் | 12th Maths : UNIT 7 : Applications of Differential Calculus
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 7 : வகை நுண்கணிதத்தின் பயன்பாடுகள்
பயன்பாடுகள் (Applications) சராசரி மதிப்புத் தேற்றம்
பயன்பாடுகள் (Applications)
எடுத்துக்காட்டு 7.26
ஒரு சுமை ஊர்தி சுங்கச் சாவடி சாலையில் மணிக்கு 80 கி.மீ வேகத்தில் செல்கிறது. அந்த சுமை ஊர்தி 2 மணி நேரத்தில் 164 கி.மீ பயணத்தை நிறைவு செய்கிறது. சுங்கச் சாவடி சாலை முடிவில் வேகக் கட்டுப்பாட்டை மீறியதற்கான அத்தாட்சி சீட்டு ஓட்டுனருக்கு வழங்கப்படுகின்றது. அவர் வேகக் கட்டுப்பாட்டை மீறியதை சராசரி மதிப்புத் தேற்றத்தின் துணை கொண்டு நியாயப்படுத்துக.
தீர்வு
't’ மணி நேரத்தில் ஓட்டுனர் கடந்த தொலைவு f (t) என்க. f (t) ஆனது [0,2] -ல் தொடர்ச்சியானது மற்றும் (0, 2) -ல் வகையிடத்தக்கது. மேலும், f (0) = 0 மற்றும் f (2) = 164. சராசரி மதிப்புத் தேற்றத்தைப் பயன்படுத்த, C என்ற காலத்தை f'(c) = 164 – 0 / 2 - 0 = 82 > 80
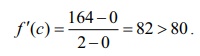
எனுமாறு காணலாம்.
எனவே, அந்த 2 மணி நேரத்தில் ஏதேனும் ஒரு கண நேரத்தில் அந்த ஓட்டுநர் 80 கி.மீ./ம வேகத்தில் பயணம் செய்திருக்க வேண்டும். ஆகவே, அவருக்கு வேகக் கட்டுப்பாட்டை மீறியதற்கான அத்தாட்சி சீட்டு வழங்கியது நியாயமே.
எடுத்துக்காட்டு 7.27
f (x) என்ற வகையிடத்தக்க சார்பு f'(x) ≤ 29 மற்றும் f (2) = 17 என்றவாறு உள்ளது எனில், f(7) -ன் அதிகபட்ச மதிப்பினைக் காண்க.
தீர்வு
சராசரி மதிப்புத் தேற்றப்படி 'C'∈ (2,7) -ஐ
f(7) - f(2) / 7 - 2 = f'(c) ≤ 29 எனக் காணலாம்.
ஆகவே, f (7) ≤ 5 × 29 + 17 = 162
எனவே, f (7) -ன் அதிகபட்ச மதிப்பு 162 ஆகும்.
எடுத்துக்காட்டு 7.28
சராசரி மதிப்புத் தேற்றத்தைப் பயன்படுத்தி,
|sin α – sin β| ≤ |α - β | α , β ∈ R என நிறுவுக.
தீர்வு
f (x) = sinx என்பது அனைத்து திறந்த இடைவெளியிலும் வகையிடத்தக்கதாகும். மூடிய இடைவெளி [α , β]-வை கருதுக. சராசரி மதிப்புத் தேற்றத்தைப் பயன்படுத்த C∈ (α , β) -ஐ
sin β - sin α / β - α = f'(c) = cos(c) எனக் காணலாம்.
எனவே |sin α - sinβ / α - β | = |cos(c) ≤ 1
ஆகவே , |sin α -sin β| ≤ |α-β|
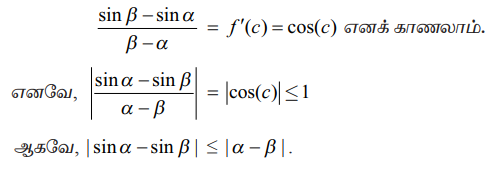
குறிப்புரை
β = 0 எனக் கொண்டால், |sin α | ≤ | α | என கிடைக்கும்.
எடுத்துக்காட்டு 7.29
ஒரு உறைவிப்பானில் இருந்து ஒரு வெப்ப நிலைமானி எடுக்கப்பட்டு கொதிக்கும் நீரில் வைக்கப்பட்டது. - 10°C-லிருந்து 100°C-க்கு உயர்த்த வெப்பநிலைமானிக்கு 22 வினாடிகள் ஆகிறது. ஏதேனும் ஒரு நேரம் t-யில் வெப்பநிலை மாறுபாட்டு வீதம் 5°C /வினாடி ஆக இருக்கும் எனக்காட்டுக.
தீர்வு
t என்ற நேரத்தில் வெப்பநிலையை f (t) என்க. சராசரி மதிப்புத் தேற்றத்தின்படி,
f'(c) = f (b) - f (a) / b - a
= 100 - (-10) / 22
= 110 / 22
= 5°C / வினாடி.
ஆகவே, ஏதேனும் ஒரு நேரம் t-யில் வெப்பநிலை மாறுபாட்டு வீதம் 5°C/வினாடி ஆகும்.