கேள்விகளுக்கான பதில்கள், தீர்வுகள் - வட்டம் (Circle): எடுத்துக்காட்டு கணக்குகள் | 12th Maths : UNIT 5 : Two Dimensional Analytical Geometry II
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 5 : இருபரிமாண பகுமுறை வடிவியல்−II
வட்டம் (Circle): எடுத்துக்காட்டு கணக்குகள்
வட்டம் (Circle): எடுத்துக்காட்டு கணக்குகள்
எடுத்துக்காட்டு 5.1
மையம் (−3, −4) மற்றும் ஆரம் 3 அலகுகள் கொண்ட வட்டத்தின் பொதுவடிவச் சமன்பாடு காண்க.
தீர்வு
வட்டத்தின் திட்ட வடிவச் சமன்பாடு (x − h)2 + (y − k)2 = r2
⇒ (x − (−3))2 + (y − (−4))2 = 32
⇒ (x + 3) 2 + (y + 4)2 = 32
⇒ x2 + y2 + 6x + 8y +16 = 0 இது பொது வடிவம் ஆகும்.
எடுத்துக்காட்டு 5.2
x2 + y2 =16 என்ற வட்டத்தின் நாண் 3x + y + 5 = 0−ஐ விட்டமாகக் கொண்ட வட்டத்தின் சமன்பாடு காண்க.
தீர்வு
தேற்றம் 5.1−ன் படி x2 + y2 =16 என்ற வட்டமும் 3x + y + 5 = 0 என்ற நேர்கோடும் வெட்டும் புள்ளிவழிச் செல்லும் வட்டத்தின் சமன்பாடு x2 + y2 – 16 + λ(3x + y + 5) = 0. இந்த வட்டத்தின் மையம் (−3λ/2 , −λ/2) . இது 3x + y + 5 = 0 என்ற கோட்டின் மீதுள்ளதால்
3(−3λ/2) − λ/2 + 5 = 0,
⇒ −9λ/2 − λ/2 + 5 = 0,
⇒ −5λ + 5 = 0,
⇒ λ = 1.
எனவே, தேவையான வட்டத்தின் சமன்பாடு x2 + y2 + 3x + y – 11 = 0.
எடுத்துக்காட்டு 5.3
x2 + y2 − 6x + 4y + c = 0 என்ற வட்டத்திற்கு c−ன் எல்லா மதிப்புகளுக்கும் x + y – 1 = 0 என்ற நேர்க்கோடு விட்டமாக அமையுமா எனத் தீர்மானிக்க.
தீர்வு
கொடுக்கப்பட்ட வட்டத்தின் மையம் (3,−2). இது x + y – 1 = 0 −ல் உள்ளது. எனவே x + y – 1 = 0 என்ற கோடு c −இன் எல்லா மதிப்பிற்கும் வட்டத்தின் மையம் வழிச்செல்லும் ஆதலால் x + y − 1 = 0 என்ற கோடு c−இன் எல்லா மதிப்பிற்கும் வட்டத்தின் விட்டமாக அமையும்.
எடுத்துக்காட்டு 5.4
(−4, −2) மற்றும் (1, 1) என்ற புள்ளிகளை விட்டத்தின் முனைகளாகக் கொண்ட வட்டத்தின் பொதுச் சமன்பாடு காண்க.
தீர்வு
தேற்றம் 5.2 −ன் படி (x1, y1) மற்றும் (x2, y2) என்ற புள்ளிகளை விட்டத்தின் முனைகளாகக் கொண்ட வட்டத்தின் சமன்பாடு (x − x1)(x – x2) + (y − y1)(y – y2) = 0
⇒ (x + 4)(x − 1) + (y + 2)(y − 1) = 0
எனவே தேவையான வட்டத்தின் சமன்பாடு x2 + y2 + 3x + y − 6 = 0.
எடுத்துக்காட்டு 5.5
x2 + y2 − 6x − 8y + 12 = 0 என்ற வட்டத்தைப் பொறுத்து (2,3) என்ற புள்ளியின் நிலையை ஆராய்க.
தீர்வு
x12 + y12 + 2gx1 + 2fy1 + c = 22 + 32 – (6 × 2) – (8 × 3) + 12,
= 4 + 9 – 12 – 24 + 12 = −11 < 0.
எனவே புள்ளி (2,3) தேற்றம் 5.3−ன் படி வட்டத்திற்கு உள்ளே அமையும்.
எடுத்துக்காட்டு 5.6
3x + 4y − 12 = 0 என்ற நேர்க்கோடு ஆய அச்சுகளை A மற்றும் B என்ற புள்ளிகளில் சந்திக்கின்றது. கோட்டுத்துண்டு AB −ஐ விட்டமாகக் கொண்ட வட்டத்தின் சமன்பாடு காண்க.
தீர்வு
நேர்க்கோடு 3x + 4y = 12 −ஐ வெட்டுத்துண்டு வடிவில் எழுத x/4 + y/3 = 1 எனக் கிடைக்கும். எனவே புள்ளிகள் A மற்றும் B முறையே (4, 0) மற்றும் (0, 3).
வட்டத்தின் சமன்பாடு விட்ட வடிவம்
(x − x1)(x – x2) + (y − y1)(y – y2) = 0
(x − 4) (x − 0) + (y − 0)(y − 3) = 0
x2 + y2 − 4x − 3y = 0.
எடுத்துக்காட்டு 5.7
ஒரு நேர்க்கோடு 3x + 4y + 10 = 0, மையம் (2,1) உள்ள ஒரு வட்டத்தில் 6 அலகுகள் நீளமுள்ள ஒரு நாணை வெட்டுகின்றது. அந்த வட்டத்தின் பொதுச் சமன்பாடு காண்க.
தீர்வு
மையம் (2, 1) உடைய வட்டத்தில் 3x + 4y + 10 = 0 என்ற நேர்க்கோடு AB என்ற நாணை வெட்டுகின்றது. AB −ன் மையப்புள்ளி M என்க.
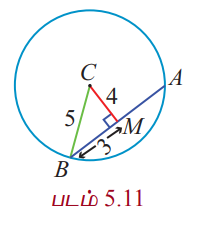
AM = BM = 3. BMC ஒரு செங்கோண முக்கோணம்
CM = |3(2) + 4(1) + 10| / √[32 + 42] = 4.
பிதாகரஸ் தேற்றப்படி BC2 = BM2 + MC2 = 32 + 42 = 25 .
BC = 5 = ஆரம்
தேவையான வட்டத்தின் சமன்பாடு (x − 2)2 + (y − 1)2 = 52
அதாவது x2 + y2 − 4x − 2y − 20 = 0 .
எடுத்துக்காட்டு 5.8
ஆரம் 3 அலகுகள் கொண்ட ஒரு வட்டம் ஆய அச்சுகளைத் தொட்டுச் செல்கின்றவாறு உருவாகும் அனைத்து வட்டங்களின் பொதுச் சமன்பாடுகளையும் காண்க.
தீர்வு
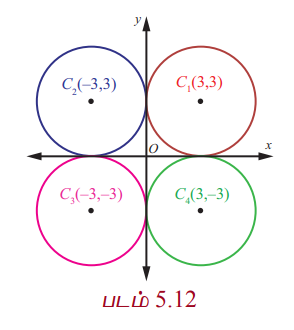
வட்டம் இரு அச்சுகளையும் தொட்டுச் செல்வதால் அச்சுகளிலிருந்து வட்டத்தின் மையத்திற்கு உள்ள தூரம் 3 அலகுகள். எனவே மையம் (±3, ±3) ஆக இருக்கும். அதனால் ஆரம் 3 உடைய நான்கு வட்டங்களின் சமன்பாடுகள் x2 + y2 ± 6x ± 6y + 9 = 0 ஆகும்.
எடுத்துக்காட்டு 5.9
ஒரு வட்டத்தின் சமன்பாடு 3x2 + (a + 1)y2 + 6x − 9y + a + 4 = 0 எனில் அதன் மையம், ஆரம் காண்க.
தீர்வு
x2 −ன் கெழு = y2 −ன் கெழு (இருபடிச் சமன்பாட்டின் பண்பு (ii)−ன் படி)
ஆதலால் 3 = a + 1, a = 2 எனக் கிடைக்கின்றது. எனவே வட்டத்தின் சமன்பாடு
3x2 + 3y2 + 6x − 9y + 6 = 0
x2 + y2 + 2x − 3y + 2 = 0
மையம் (−1, 3/2) மற்றும் ஆரம் r = √[ 1+ 9/4 – 2] = √5/2 .
எடுத்துக்காட்டு 5.10
(1, 1), (2, −1), மற்றும் (3, 2) என்ற மூன்று புள்ளிகள் வழிச்செல்லும் வட்டத்தின் சமன்பாடு காண்க.
தீர்வு
வட்டத்தின் பொதுச் சமன்பாடு x2 + y2 + 2gx + 2fy + c = 0 …..(1)
இது (1, 1), (2, −1) மற்றும் (3, 2) என்ற புள்ளிகள் வழிச்செல்வதால்
2g + 2f + c = −2, …….(2)
4g − 2f + c = −5, …….(3)
6g + 4f + c = −13. …….(4)
(2) − (3) −இலிருந்து −2g + 4f = 3. …..... (5)
(4) − (3) −இலிருந்து 2g + 6f = −8. …….(6)
(5) + (6) −இலிருந்து f = −1/2 என கிடைக்கும் மதிப்பை (6)இல் பிரதியிட g = −5/2, f, g இன் மதிப்புகளை (2)இல் பிரதியிட c = 4 எனவும் கிடைக்கிறது.
எனவே தேவையான வட்டத்தின் சமன்பாடு
x2 + y2 + 2(−5/2)x + 2(−1/2)y + 4 = 0
அதாவது x2 + y2 − 5x – y + 4 = 0.
எடுத்துக்காட்டு 5.11
x2 + y2 = 25 என்ற வட்டத்திற்கு P(−3, 4) −இல் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளைக் காண்க.
தீர்வு
P(x1, y1) −இல் தொடுகோட்டுச் சமன்பாடு xx1 + yy1 = a2 .
அதாவது, (−3, 4)−இல் x(−3) + y(4) = 25
−3x + 4y = 25
செங்கோட்டுச் சமன்பாடு xy1 − yx1 = 0
அதாவது, 4x + 3y = 0 .
எடுத்துக்காட்டு 5.12
y = 4x + c என்ற நேர்க்கோடு x2 + y2 = 9 என்ற வட்டத்தின் தொடுகோடு எனில் c −ன் மதிப்புக் காண்க.
தீர்வு
y = mx + c என்ற நேர்க்கோடு x2 + y2 = a2 என்ற வட்டத்தின் தொடுகோடாக இருக்கக் கட்டுப்பாடு c2 = a2 (1 + m2).
எனவே, c = ±√[9(1+16)]
அல்லது c = ±3√17.
எடுத்துக்காட்டு 5.13
பாசன வாய்க்கால் மீது அமைந்த சாலையில் 20மீ அகலமுடைய இரண்டு அரைவட்ட வளைவு நீர்வழிகள் அமைக்கப்பட்டன. அவற்றின் துணைத்தூண்களின் அகலம் 2 மீ. படம் 5.16−ஐப் பயன்படுத்தி அந்த வளைவுகளின் மாதிரிக்கான சமன்பாடுகளைக் காண்க.
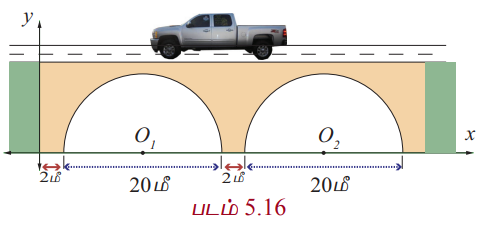
தீர்வு
அரைவட்ட வளைவு வழிகளின் மையப்புள்ளிகள் O1 மற்றும் O2 என்க.
முதல் வளைவு வழியின் மையம் O1 (12, 0) மற்றும் r = 10. இதிலிருந்து அந்த அரைவட்டத்தைக் குறிக்கும் சமன்பாடு
(x − 12)2 + (y − 0)2 = 102
⇒ x2 + y2 − 24x + 44 = 0, y > 0.
இரண்டாம் வளைவு வழியின் மையம் O2 (34, 0) மற்றும் ஆரம் r = 10. முதல் வளைவு போல இரண்டாம் வளைவு வழியின் சமன்பாடு
(x − 34)2 + y2 = 102
⇒ x2+ y2 − 68x + 1056 = 0, y > 0.