நீள்வட்டம் (Ellipse)

3. நீள்வட்டம் (Ellipse)

ஒரு தளத்தில், ஒரு நகரும் புள்ளிக்கும் குவியத்திற்கும் உள்ள தூரம் அந்த நகரும் புள்ளிக்கும் இயக்குவரைக்கும் உள்ள தூரத்தைவிடக் குறைவாக e என்ற மாறாத விகிதமுடையதாக (0 < e < 1) இருப்பின் அந்த நகரும் புள்ளியின் நியமப்பாதை ஓர் நீள்வட்டமாகும்.

(i) மையம் (0,0) உடைய நீள்வட்டச் சமன்பாட்டின் திட்ட வடிவம்

குவியம் S, இயக்குவரை l, மையத் தொலைத்தகவு e  (0 < e < 1) மற்றும் நகரும் புள்ளி P(x, y) என்க. இயக்குவரை l −க்குச் செங்குத்தாக SZ மற்றும் PM வரைக. 

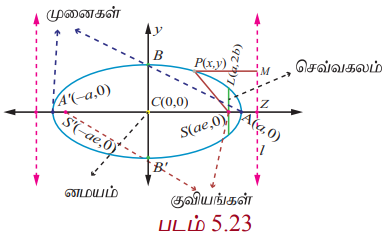
A மற்றும் A' என்ற புள்ளிகள் முறையே SZ −ஐ உட்புறமாகவும் வெளிப்புறமாகவும் e : 1 என்ற விகிதத்தில் பிரிக்கின்றன என்க. AA' = 2a என்க. AA'−ன் மையக்குத்துக்கோடு AA' −ஐ C−இல் வெட்டுகின்றது என்க.

C−ஐ மையமாகவும் CZ−இன் நீட்சியை x −அச்சாகவும், AA'−இன் மையக் குத்துக்கோட்டை y −அச்சாகவும் கொள்க. அதனால் CA = a மற்றும் CA' = a ஆகும்.

வரையறையின்படி

 (2) + (1) இதிலிருந்து CZ = a/e மற்றும் (2)−(1) இதிலிருந்து CS = ae எனக்கிடைக்கும்.

எனவே M என்பது (a/e , y) மற்றும் S என்பது (ae, 0) ஆக இருக்கும்.

வரையறையின்படி SP/PM = e  அல்லது SP2 = e2PM2

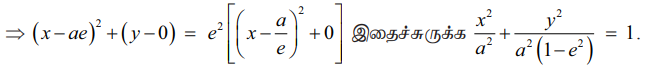
1 − e2 மிகை மதிப்பு எனவே, b2 = a2 (1− e) எனவும் ae = c, b2 = a2 − c2 எனக்கொண்டால்

இப்போது P −ன் நியமப்பாதை x2/a2 + y2/b2 = 1 எனக்கிடைக்கும். இது நீள்வட்டச் சமன்பாட்டின் திட்டவடிவம் ஆகும். மேலும் வளைவரை x, y அச்சுகளுக்கு சமச்சீராக உள்ளதைக் கவனிக்கவும்.

வரையறை 5.4

(1) கோட்டுத்துண்டு AA' என்பது நெட்டச்சு மற்றும் அதன் நீளம் 2a ஆகும்.

(2) கோட்டுத்துண்டு BB' என்பது குற்றச்சு மற்றும் அதன் நீளம் 2b ஆகும். 

(3) கோட்டுத்துண்டு CA = கோட்டுத்துண்டு CA' = அரை நெட்டச்சு = a மற்றும் கோட்டுத்துண்டு CB = கோட்டுத்துண்டு CB' = அரை குற்றச்சு = b . 

(4) சமச்சீர் தன்மையினால் குவியம் S'(−ae, 0) மற்றும் இயக்குவரை l', x = − a/e எடுத்துக்கொண்டாலும் அதே நீள்வட்டம் கிடைக்கும்.

இதன் மூலம் நீள்வட்டத்திற்கு S(ae, 0) மற்றும் S′(−ae, 0) என இரு குவியங்களும் A(a, 0) மற்றும் A'(−a, 0) என இரு முனைகளும், x = a/e மற்றும் x = − a/e என இரு இயக்குவரைகளும் உள்ளதைக் காணலாம்.

எடுத்துக்காட்டு 5.15

நீள்வட்டம் 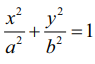 −ன் செவ்வகல நீளம் காண்க.

தீர்வு

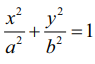   என்ற நீள்வட்டத்தின் செவ்வகலம் LL' (படம் 5.22) S(ae,0) வழிச்செல்கின்றது.

எனவே, L (ae, y1) நீள்வட்டத்தின் மீதுள்ளது.

அதனால்,

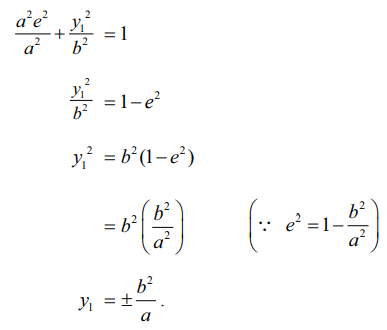
அதாவது செவ்வகலத்தின் முனைப்புள்ளிகள் L மற்றும் L' முறையே [ae, b2/a] மற்றும் [ae, −b2/a] ஆகும்.

செவ்வகலத்தின் நீளம் LL' = 2b2/a

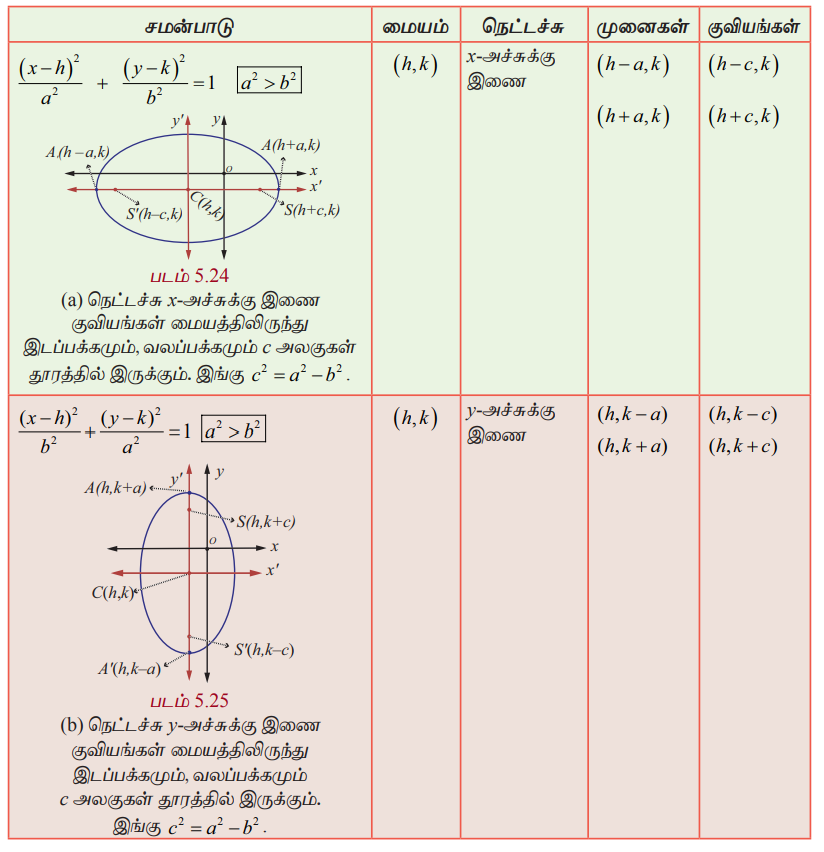
(ii) மையம் (h,k) உடைய நீள்வட்டத்தின் வகைகள் (Types of ellipses with centre at (h,k)) 

(அ) நெட்டச்சு x−அச்சுக்கு இணை (Major axis parallel to the x−axis)

நீள்வட்டத்தின் சமன்பாடு (படம் 5.24) 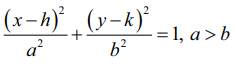ஆகும்.

நெட்டச்சின் நீளம் 2a மற்றும் குற்றச்சின் நீளம் 2b ஆகும். முனைப்புள்ளிகள் (h + a , k) மற்றும் (h − a, k), மேலும் குவியங்கள் (h + c, k) மற்றும் (h − c, k) ஆக இருக்கும். இங்கு c2 = a2 − b2. 

(ஆ) நெட்டச்சு y−அச்சுக்கு இணை (Major axis parallel to the y−axis)

நீள்வட்டத்தின் சமன்பாடு (படம் 5.25) 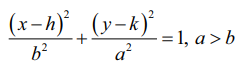  ஆகும்.

நெட்டச்சின் நீளம் 2a, குற்றச்சின் நீளம் 2b ஆகும். முனைப்புள்ளிகள் (h, k + a) மற்றும் (h, k − a) மேலும் குவியங்கள் (h, k + c) மற்றும் (h, k − c) ஆக இருக்கும். இங்கு c2 = a2 − b2.

தேற்றம் 5.5

நீள்வட்டத்தின் மீதுள்ள ஏதேனும் ஒரு புள்ளியின் குவித்தொலைவுகளின் கூடுதல் அதன் நெட்டச்சின் நீளத்திற்குச் சமம்.

நிரூபணம்

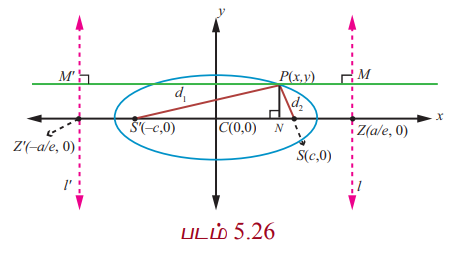
P(x, y) என்பது நீள்வட்டம் 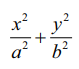  −ன் மீதுள்ள ஏதேனும் ஒரு புள்ளி என்க.

P −ன் வழியாக l , l’ இயக்குவரைகளுக்கு செங்குத்தாக MM' வரைக.

x −அச்சுக்கு செங்குத்தாக PN வரைக.

வரையறையிலிருந்து

SP = ePM

= eNZ

= e[CZ − CN]

= e[a/2 − x] = a – ex      ………….(1)

SP' = ePM'

= e[CN + CZ']

= e[x + a/e] = ex + a               ………….(2)

SP + S'P = a – ex + a + ex = 2a

குறிப்புரை

b = a ஆக இருக்கும்போது 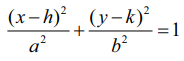  என்ற சமன்பாடு (x − h)2 + (y − k)2 = a2 என மாறும். இது மையம் (h, k) மற்றும் ஆரம் a உடைய வட்டத்தின் சமன்பாடு ஆகும்.

b = a ஆக இருக்கும் போது 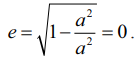 எனவே வட்டத்தின் மையத்தொலைத் தகவு பூச்சியம்.

SP/PM = 0 ⇒ PM → ∞. அதாவது வட்டத்தின் இயக்குவரை (முடிவிலியில்) கந்தழியில் உள்ளது எனலாம்.

குறிப்புரை

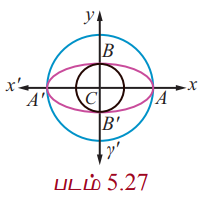
ஒரு நீள்வட்டத்தின் நெட்டச்சை விட்டமாகக் கொண்ட வட்டம் துணைவட்டம் அல்லது சுற்றுவட்டம் எனப்படும். மேலும் குற்றச்சை விட்டமாகக்கொண்ட வட்டம் உள்வட்டம் எனப்படும். அவற்றின் சமன்பாடுகள் முறையே x2 + y2 = a2 மற்றும் x2 + y2 = b2 ஆகும்.