வட்டத்தின் மீதமைந்த P என்ற புள்ளியில் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகள் (Equations of tangent and normal at a point P on a given circle)

2. வட்டத்தின் மீதமைந்த P என்ற புள்ளியில் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகள் (Equations of tangent and normal at a point P on a given circle)

ஒரு நேர்கோடு வட்டத்தை ஒரே ஒரு புள்ளியில் தொட்டுச்சென்றால் அது தொடுகோடாகும். மேலும் அந்த தொடுகோட்டுக்குச் செங்குத்தாகவும் தொடுபுள்ளி வழியாகவும் செல்லும் கோடு செங்கோடாகும்.

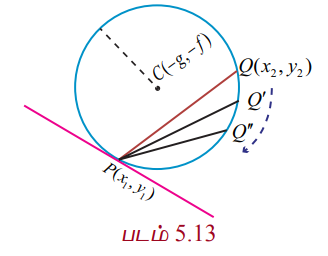
P(x1 , y1) மற்றும் Q(x2 , y2) என்பன x2 + y2 + 2gx + 2fy + c = 0 என்ற வட்டத்தின் மீதமைந்த இரு புள்ளிகள் என்க.

எனவே, x12 + y12 + 2gx1 + 2fy1 + c  = 0  ………(1)

மற்றும் x22 + y22 + 2gx2 + 2fy2 + c  = 0  ……….(2)

(2)−(1)−இலிருந்து

x22 − x12 + y22 − y12 + 2g(x2 – x1) + 2f (y2 – y1) = 0

(x2 – x1)(x2 + x1 + 2g) + (y2 – y1)(y2 + y1 + 2f) = 0

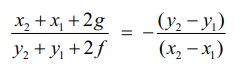
இதனால் PQ −இன் சாய்வு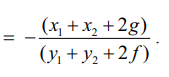

Q என்ற புள்ளி P−ஐ நோக்கி நகரும்போது PQ என்ற நாண் P என்ற புள்ளிக்கான தொடுகோடாக மாறும்.

தொடுகோட்டின் சாய்வு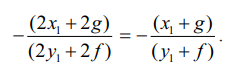

எனவே தொடுகோட்டின் சமன்பாடு y − y1 = –[(x1 + g)/(y1 + f)] (x – x1) −இலிருந்து,

yy1 + fy − y12 − fy1 + xx1 − x12 + gx − gx1 = 0 

xx1 + yy1 + gx + fy − (x12 + y12 + gx1 + fy1) = 0  ……….(1)

(x1, y1) என்ற புள்ளி வட்டத்தின் மீதுள்ளதால் x12 + y12 + 2gx1 + 2fy1 + c  =0 

எனவே, −( x12 + y12 + 2gx1 + 2fy1) = gx1 + fy1 + c   ……….(2)

இதனால் (x1, y1) என்ற புள்ளியில் தொடுகோட்டின் சமன்பாடு

xx1 + yy1 + g(x + x1) + f (y + y1) + c = 0 ஆகும்.

மேலும் செங்கோட்டின் சமன்பாடு (y − y1) = [(y1 + f) / (x1 + g)] (x − x1) 

⇒  (y − y1) (x1 + g) = (y1 + f)(x − x1)

⇒ x1 (y − y1 ) + g(y − y1) = y1 (x − x1) + f(x − x1)

⇒ yx1 − xy1 + g (y − y1) − f(x − x1) = 0 சமன்பாடுகள்

குறிப்புரை

(1) x2 + y2 = a2 என்ற வட்டத்திற்கு (x1, y1) என்ற புள்ளியில் தொடுகோட்டுச் சமன்பாடு xx1 + yy1 = a2.

(2) x2 + y2 = a2 என்ற வட்டத்திற்கு (x1, y1) என்ற புள்ளியில் செங்கோட்டுச் சமன்பாடு xy1 + yx1 = 0.

(3) செங்கோடு வட்டத்தின் மையம் வழிச் செல்லும்.