y = mx + c என்ற நேர்க்கோடு x2 + y2 = a2 என்ற வட்டத்தின் தொடுகோடாக இருக்க கட்டுப்பாடு மற்றும் தொடும் புள்ளி காணல் (Condition for the line y = mx + c to be a tangent to the circle x2 + y2 = a2 and finding the point of contact)

3. y = mx + c என்ற நேர்க்கோடு  x2 + y2 = a2 என்ற வட்டத்தின் தொடுகோடாக இருக்க கட்டுப்பாடு மற்றும் தொடும் புள்ளி காணல் (Condition for the line y = mx + c to be a tangent to the circle x2 + y2 = a2 and finding the point of contact)

y = mx + c என்ற நேர்க்கோடு x2 + y2 = a2 என்ற வட்டத்தைத் தொடுகின்றது என்க. இந்த வட்டத்தின் மையம் மற்றும் ஆரம் முறையே (0,0) மற்றும் a ஆகும்.

(i) ஒரு நேர்க்கோடு தொடுகோடாக இருக்கக் கட்டுப்பாடு (Condition for a line to be tangent) 

(0, 0) என்ற புள்ளியிலிருந்து y – mx – c = 0 என்ற நேர்கோட்டிற்கான செங்குத்து தூரம்

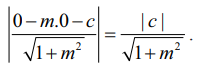இது ஆரத்திற்குச் சமம்.

எனவே |c| / √[1 + m2] = a அல்லது c2 = a2 (1 + m2) .

இதனால் y = mx + c என்ற நேர்கோடு x2 + y2 = a2 என்ற வட்டத்திற்குத் தொடுகோடாக அமைய கட்டுப்பாடு c2 = a2 (1 + m2) .

(ii) தொடுபுள்ளி (Point of contact)

y = mx+c என்ற நேர்கோடு x2 + y2 = a2 என்ற வட்டத்தை தொடும் புள்ளி (x1, y1) எனில்

y1 = mx1 +c.                           ..... (1)

(x1, y1) −இல் தொடுகோட்டின் சமன்பாடு xx1 + yy1 = a2

yy1 = −xx1 + a2                                   ..... (2)

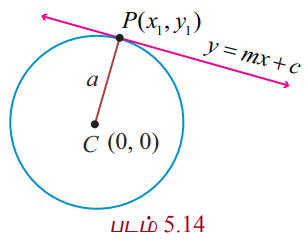
சமன்பாடு (1) மற்றும் (2) ஒரே நேர்க்கோட்டைக் குறிக்கின்றன.

எனவே கெழுக்கள் விகித சமமாக இருக்கும்.

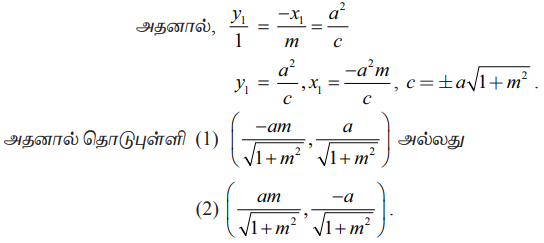
குறிப்பு

P என்ற புள்ளியில் வட்டத்தின் தொடுகோட்டுச் சமன்பாடு y = mx ± a √[1 + m2].

தேற்றம் 5.4

x2 + y2 = a2 என்ற வட்டத்திற்கு வெளியே உள்ள ஒரு புள்ளியிலிருந்து இரு தொடுகோடுகள் வரையலாம்.

நிரூபணம்

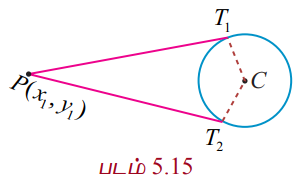
கொடுக்கப்பட்ட புள்ளி P(x1, y1) என்ற புள்ளி வட்டத்திற்கு வெளியே உள்ளது என்க. தொடுகோட்டுச் சமன்பாடு y = mx ± a√[1 + m2]. இது (x1, y1) வழிச்செல்லும். எனவே

y1 = mx1 ± a√[1 + m2]

y1 − mx1 =  a √[1 + m2] இருபுறமும் வர்க்கப்படுத்த, 

(y1 − mx1)2 = a2 (1 + m2)

y12 + m2x12 − 2mx1 y1 − a2 – a2m2 = 0

m2 (x12 − a2) − 2mx1 y1 + (y12 − a2) = 0.

m−ன் இந்த இருபடிச் சமன்பாடு, m க்கு இரண்டு மதிப்புகள் தரும். இந்த இருமதிப்புகள் வட்டத்திற்கான இரு தொடுகோடுகளைத் தரும்.

குறிப்பு

(1) புள்ளி (x1, y1) வட்டத்திற்கு வெளியில் அமையுமானால் இரு தொடுகோடுகளும் மெய்யானவையாகும்.

(2) புள்ளி (x1, y1) வட்டத்திற்கு உள்ளே அமையுமானால் இரு தொடுகோடுகளும் கற்பனையானவையாகும்.

(3) புள்ளி (x1, y1) வட்டத்தின் மீது அமையுமானால் இரு தொடுகோடுகளும் ஒன்றாக இணையும். 

எடுத்துக்காட்டு 5.11

x2 + y2 = 25 என்ற வட்டத்திற்கு P(−3, 4) −இல் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளைக் காண்க.

தீர்வு

P(x1, y1) −இல் தொடுகோட்டுச் சமன்பாடு xx1 + yy1 = a2 .

அதாவது, (−3, 4)−இல் x(−3) + y(4) = 25

   −3x + 4y = 25

செங்கோட்டுச் சமன்பாடு xy1 − yx1 = 0

அதாவது, 4x + 3y = 0 .

எடுத்துக்காட்டு 5.12

y = 4x + c என்ற நேர்க்கோடு x2 + y2 = 9 என்ற வட்டத்தின் தொடுகோடு எனில் c −ன் மதிப்புக் காண்க.

தீர்வு

y = mx + c என்ற நேர்க்கோடு x2 + y2 = a2 என்ற வட்டத்தின் தொடுகோடாக இருக்கக் கட்டுப்பாடு c2 = a2 (1 + m2).

எனவே, c = ±√[9(1+16)]

அல்லது c = ±3√17.

எடுத்துக்காட்டு 5.13

பாசன வாய்க்கால் மீது அமைந்த சாலையில் 20மீ அகலமுடைய இரண்டு அரைவட்ட வளைவு நீர்வழிகள் அமைக்கப்பட்டன. அவற்றின் துணைத்தூண்களின் அகலம் 2 மீ. படம் 5.16−ஐப் பயன்படுத்தி அந்த வளைவுகளின் மாதிரிக்கான சமன்பாடுகளைக் காண்க.

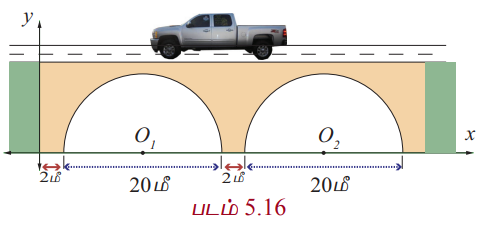
தீர்வு

அரைவட்ட வளைவு வழிகளின் மையப்புள்ளிகள் O1 மற்றும் O2 என்க.

முதல் வளைவு வழியின் மையம் O1 (12, 0) மற்றும் r = 10. இதிலிருந்து அந்த அரைவட்டத்தைக் குறிக்கும் சமன்பாடு

(x − 12)2 + (y − 0)2 = 102

⇒ x2 + y2 − 24x + 44 = 0, y > 0.

இரண்டாம் வளைவு வழியின் மையம் O2  (34, 0) மற்றும் ஆரம் r = 10. முதல் வளைவு போல இரண்டாம் வளைவு வழியின் சமன்பாடு 

(x − 34)2 + y2 = 102

⇒ x2+ y2 − 68x + 1056 = 0, y > 0.