பாடச்சுருக்கம்

பாடச்சுருக்கம்

(1) வட்டச் சமன்பாட்டின் திட்டவடிவம் (x − h)2 + (y − k)2 = r2.

(i) மையம் (h, k)

(ii) ஆரம் ‘r’

(2) வட்டச் சமன்பாட்டின் பொது வடிவம் x2 + y2 + 2gx + 2fy + c = 0

(i) மையம் (−g, −f)

(ii) ஆரம் = √[g2 + ƒ2 – c]

(3) lx + my + n = 0 என்ற நேர்க்கோடும் x2 + y2 + 2gx + 2fy + c = 0 

என்ற வட்டமும் வெட்டிக் கொள்ளும் புள்ளிகள் வழியே செல்லும் வட்டத்தின் சமன்பாடு x2 + y2 + 2gx + 2fy + c + λ (lx + my + n) = 0, λ ∈ ℝ1 .

(4) ஒரு வட்டத்தின் விட்டத்தின் முனைப்புள்ளிகள் (x1, y1) மற்றும் (x2, y2) எனில் அந்த வட்டத்தின் சமன்பாடு (x − x1)(x – x2) + (y − y1)(y – y2) = 0 ஆகும்.

(5) (x1, y1) என்ற புள்ளியில் x2 + y2 + 2gx + 2fy + c = 0 என்ற வட்டத்தின் தொடுகோடுச் சமன்பாடு xx1 + yy1 + g(x + x1) + f (y + y1) + c = 0

(6) (x1, y1) என்ற புள்ளியில் x2 + y2 + 2gx + 2fy + c = 0 என்ற வட்டத்தின் செங்கோட்டுச் சமன்பாடு yx1  −  xy1 + g(y  −  y1) −   f (x  −  x1) = 0.

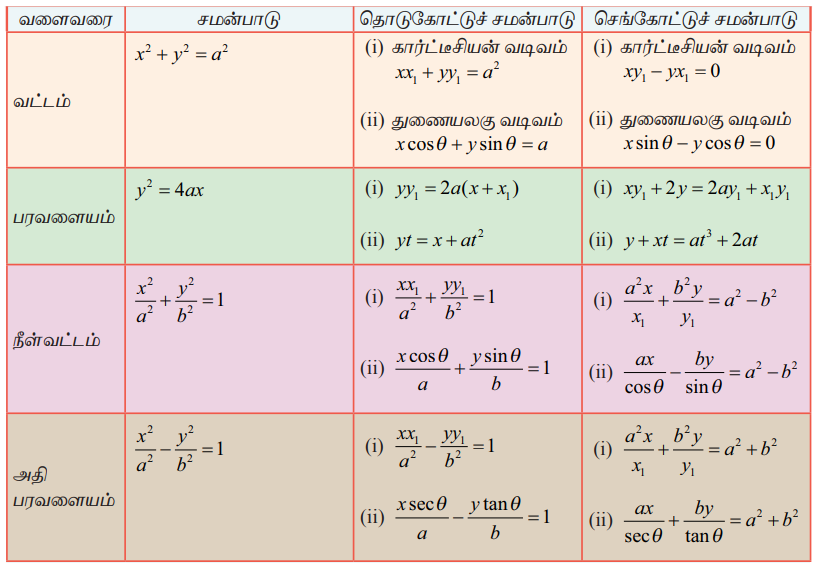
அட்டவணை 1

தொடுகோடு மற்றும் செங்கோடு

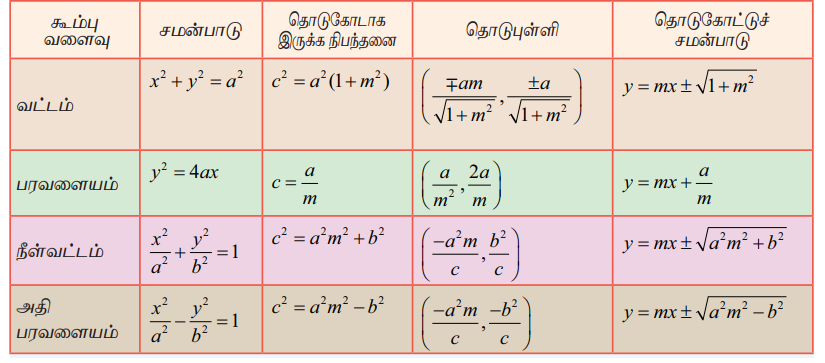
அட்டவணை 2

y = mx + c என்ற நேர்க்கோடு கூம்பு வளைகளின் தொடுகோடாக இருக்க நிபந்தனை

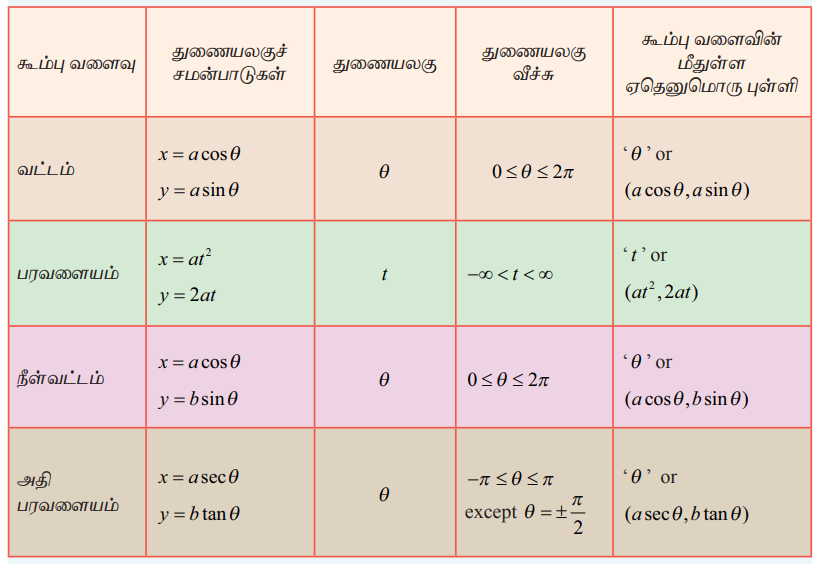
அட்டவணை 3

துணையலகு வடிவங்கள்

3. கூம்பு வளைவின் பொதுச் சமன்பாடு Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 −லிருந்து கூம்புவளைவின் வடிவங்களை அடையாளம் காணல்

(Identifying the conics from the general equation of the conic Ax2 + Bxy + Cy2 + Dx + Ey + F = 0)

இரண்டாம்படி சமன்பாட்டின் வரைபடம் பின்வரும் நிபந்தனைகளுக்கு ஏற்ப வட்டம், பரவளையம், நீள்வட்டம், அதிபரவளையம், ஒரு புள்ளி, வெற்றுக்கணம், ஒரு நேர்க்கோடு அல்லது ஒரு இரட்டை நேர்க்கோடாக இருக்கும்.

(1) A = C = 1, B = 0, D = −2h, E = −2k, F = h2 + k2 − r2 எனில் பொதுச்சமன்பாடு (x − h)2 + (y − k)2 = r2 எனக்கிடைக்கும். இது ஒரு வட்டம் ஆகும்.

(2) B = 0 மற்றும் A அல்லது C = 0 எனில், பொதுச்சமன்பாடு நாம் படித்த ஏதேனும் ஒரு பரவளையம் ஆகும்.

(3) A ≠ C மற்றும் A மற்றும் C இரண்டும் ஒரே குறியாக இருப்பின் பொதுச் சமன்பாடு நீள்வட்டத்தைத் தரும்.

(4) A ≠ C மற்றும் A மற்றும் C இரண்டும் ஒன்றுக்கொன்று எதிர்குறியாக இருக்குமானால் பொதுச் சமன்பாடு அதிபரவளையத்தைத் தரும்.

(5) A = C மற்றும் B = D = E = F = 0, எனில் பொதுச் சமன்பாடு x2 + y2 = 0 என்ற புள்ளியாக மாறும்.

(6) A = C = F மற்றும் B = D = E = 0, எனில் பொதுச் சமன்பாடு x2 + y2 + 1 = 0 என்ற வெற்றுக் கணத்தைத் தரும்.

(7) A ≠  0 அல்லது C ≠ 0 மற்றும் மற்ற கெழுக்கள் பூச்சியம் எனில் பொதுச் சமன்பாடு ஆய அச்சுகளின் சமன்பாட்டைத் தரும்.

(8) A = −C மற்றும் மற்ற அனைத்து உறுப்புகளும் பூச்சியம் எனில் பொதுச் சமன்பாடு x2 − y2 = 0 என்ற இரட்டை நேர்க்கோட்டைத் தரும்.

இணையச் செயல்பாடு (ICT CORNER)

 https://ggbm.at/vchq92pg அல்லது Scan the QR Code

இணைய உலாவியை திறக்கவும், கொடுக்கப்பட்டுள்ள உரலி/விரைவுக் குறியீட்டை தட்டச்சு செய்யவும். GeoGebra−வின் "12th Standard Mathematics" பக்கம் தோன்றும். இப்பணித்தாள் புத்தகத்தின் இடது பக்கம் உங்கள் பாடநூலுடன் தொடர்புடைய பல அத்தியாயங்கள் காணப்படும். அவற்றில் "Two Dimensional Analytical Geometry−II" எனும் அத்தியாயத்தைத் தேர்வு செய்க. இப்பொழுது இப்பாடம் தொடர்பான பல பணித்தாள்களை இப்பக்கத்தில் காண்பீர்கள். "Conic Tracing" பயிற்சித்தாளை தேர்வு செய்க.