Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ, Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ, Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї, Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ, Я«хЯ«ЋЯ»ѕЯ«ЋЯ«│Я»Ї - Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї (Hyperbola) | 12th Maths : UNIT 5 : Two Dimensional Analytical Geometry II
12 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї : Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я««Я»Ї 5 : Я«ЄЯ«░Я»ЂЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«фЯ«ЋЯ»ЂЯ««Я»ЂЯ«▒Я»ѕ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»ЇРѕњII
Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї (Hyperbola)
4. Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї (Hyperbola)
Я«њЯ«░Я»Ђ Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, Я«њЯ«░Я»Ђ Я«еЯ«ЋЯ«░Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ«ЋЯ«░Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Ћ, e (e > 1) Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я«ЙЯ«▒Я«ЙЯ«ц Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я«ЅЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ«ЋЯ«░Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«┐Я«»Я««Я«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕ Я«ЊЯ«░Я»Ї Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(i) Я««Я»ѕЯ«»Я««Я»Ї (0, 0) Я«ЅЯ«ЪЯ»ѕЯ«» Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«цЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї
A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї A' Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є SZ РѕњЯ«љ Я«ЅЯ«ЪЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«хЯ»єЯ«│Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї e : 1 Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ«┐Я«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е Я«јЯ«ЕЯ»ЇЯ«Ћ. AA' = 2a Я«јЯ«ЕЯ»ЇЯ«Ћ. AA' РѕњЯ«ЕЯ»Ї Я««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ AA' РѕњЯ«љ CРѕњЯ«ЄЯ«▓Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Ћ. CРѕњЯ«љ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї CZ РѕњЯ«ЄЯ«ЕЯ»Ї Я«еЯ»ђЯ«ЪЯ»ЇЯ«џЯ«┐Я«»Я»ѕ xРѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, AA' РѕњЯ«ЄЯ«ЕЯ»Ї Я««Я»ѕЯ«»Я«ЋЯ»Ї Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ y РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ. Я«ЁЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї CA = a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї CA' = a Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
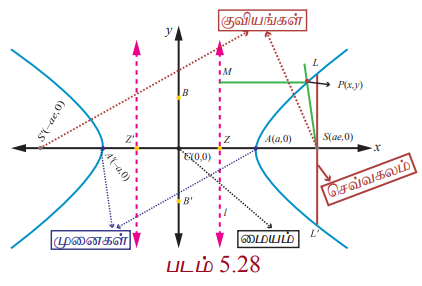
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«»Я«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ AS/AZ = e Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї AРђЎS/AРђЎZ = e Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
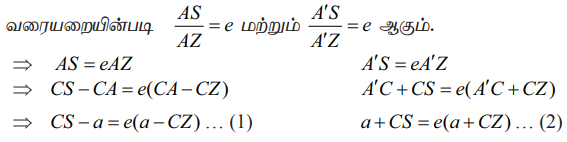
(1) + (2)РѕњЯ«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ CS = ae Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (2)Рѕњ(1)РѕњЯ«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ CZ = a/e Я«јЯ«Е Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї
Я«јЯ«ЕЯ«хЯ»Є, S РѕњЯ«ЕЯ»Ї Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕЯ«ЋЯ«│Я»Ї (ae, 0). PM = x Рѕњ a/e , Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ x Рѕњ a/e = 0 Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. P(x, y) Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐, SP/PM = e Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ SP2 = e2PM2.
Я«ЁЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї (x Рѕњ ae)2 + (y Рѕњ 0)2 = e2[x Рѕњ a/e]2
РЄњ (x Рѕњ ae)2 + y2 = (ex Рѕњ a)2
РЄњ (e2 Рѕњ1)x2 Рѕњ y2 = a2 (e2 Рѕњ 1)
РЄњ 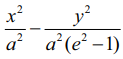 Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ a2 (e2 Рѕњ 1) = b2 Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ PРѕњЯ«ЕЯ»Ї Я«еЯ«┐Я«»Я««Я«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕ
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ a2 (e2 Рѕњ 1) = b2 Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ PРѕњЯ«ЕЯ»Ї Я«еЯ«┐Я«»Я««Я«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕ 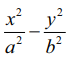 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«цЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ ae = c Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ, b2 = c2 Рѕњ a2 Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ««Я«џЯ»ЇЯ«џЯ»ђЯ«░Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«цЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ ae = c Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ, b2 = c2 Рѕњ a2 Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ««Я«џЯ»ЇЯ«џЯ»ђЯ«░Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 5.5
(1) Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ AA' Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»ЇЯ«џЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 2a Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(2) Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ BB' Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«џЯ»ЇЯ«џЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 2b Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(3) Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ CA = Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ CA' = Я«ЁЯ«░Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»ЇЯ«џЯ»Ђ = a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ CB = Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ CBРђ▓ = Я«ЁЯ«░Я»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ѕЯ«»Я«џЯ»ЇЯ«џЯ»Ђ = b Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(4) Я«џЯ««Я«џЯ»ЇЯ«џЯ»ђЯ«░Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я««Я»Ї S'(Рѕњae, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я»ѕ l', x = Рѕњ a/e Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ»Є Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ S(ae, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї S'(Рѕњae, 0) Я«јЯ«Е Я«ЄЯ«░Я»Ђ Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї A(a, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї A'(Рѕњa, 0) Я«јЯ«Е Я«ЄЯ«░Я»Ђ Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»ЂЯ««Я»Ї, x = a/e Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x = Рѕњa/e Я«јЯ«Е Я«ЄЯ«░Я»Ђ Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я»ѕЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«▓Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 2b2/a , Я«јЯ«Е Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«цЯ»ЂЯ«фЯ»ІЯ«▓ Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«цЯ»іЯ«▓Я»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї (Asymptotes)
P(x, y) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ y = f(x) Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«хЯ«│Я»ѕЯ«хЯ«░Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«јЯ«ЕЯ»ЇЯ«Ћ. P Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«Е Я«цЯ»ѓЯ«░Я««Я»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ P Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«єЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«хЯ«┐Я«▓Я«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ«┐Я«▓Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ«░Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«цЯ»іЯ«▓Я»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«БЯ»ЇЯ«ЪЯ»Ђ. Я«ЁЯ«цЯ»Є Я«џЯ««Я«»Я««Я»Ї Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ..
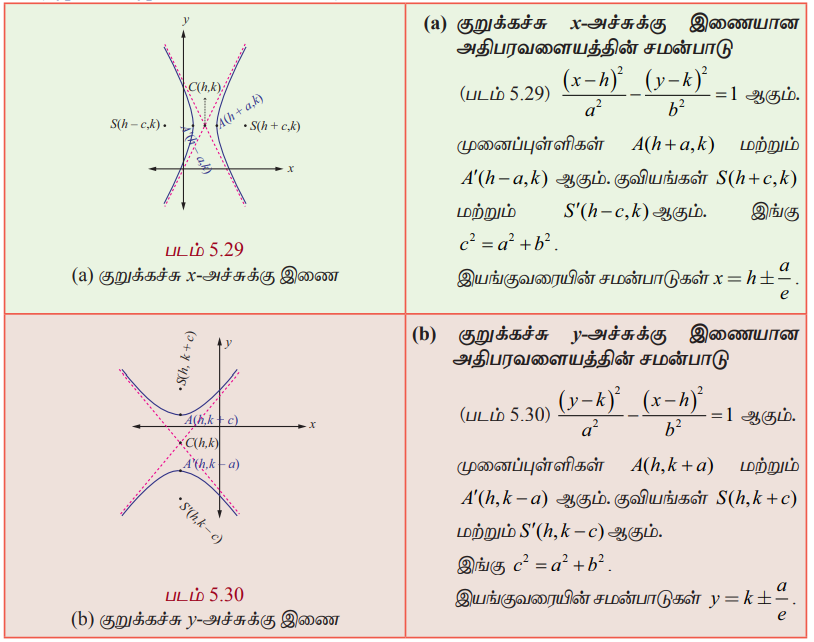
(ii) (h,k) РђЊЯ«љ Я««Я»ЂЯ«ЕЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЅЯ«ЪЯ»ѕЯ«» Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Types of Hyperbola with centre at (h, k))
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«░Я»ѕ
(1) Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»ЇЯ«џЯ»ѕ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ««Я«ЙЯ«ЋЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«цЯ»ЂЯ«БЯ»ѕЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ x2 + y2 = a2.
(2) Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я«ЙЯ«Е Я«цЯ»ѓЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ | PS РђЊ PS'| = 2a .
(Я«ЄЯ«цЯ»ѕ Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«▓Я«ЙЯ««Я»Ї.)
Я«ЄЯ«цЯ»ЂЯ«хЯ«░Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«фЯ«ЪЯ«┐Я«цЯ»ЇЯ«цЯ»ІЯ««Я»Ї. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░ Я«ЄЯ«еЯ»ЇЯ«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«хЯ«ЋЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я««Я»ЂЯ«ЪЯ«┐Я«»Я«ЙЯ«ц Я«фЯ«▓ Я«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е, Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї, Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї, Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ.
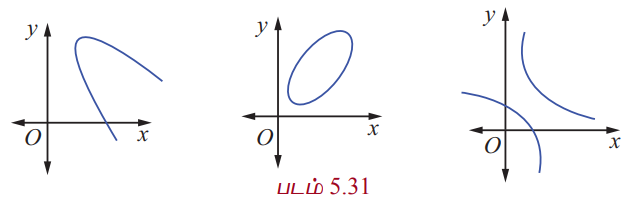
Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«хЯ«│Я»ѕЯ«хЯ«░Я»ѕЯ«ЋЯ«│Я»ѕ Я«џЯ«░Я«┐Я«»Я«ЙЯ«Е Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ»єЯ«»Я«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐ Я««Я»ѓЯ«▓Я««Я»Ї Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.16
Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я««Я»Ї (РѕњРѕџ2, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я»ѕ x = Рѕџ2 Я«ЅЯ«ЪЯ»ѕЯ«» Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
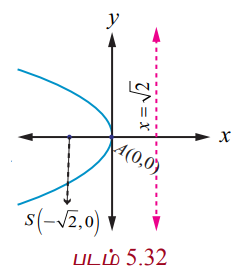
Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«цЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ««Я«џЯ»ЇЯ«џЯ»ђЯ«░Я»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ x РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЕЯ»ѕ (0, 0) Я«єЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
(y Рѕњ 0)2 = Рѕњ4Рѕџ2 (x Рѕњ 0)
РЄњ y2 = Рѕњ4Рѕџ2x.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.17
Я««Я»ЂЯ«ЕЯ»ѕ (5, Рѕњ2) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я««Я»Ї (2, Рѕњ2) Я«ЅЯ«ЪЯ»ѕЯ«» Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
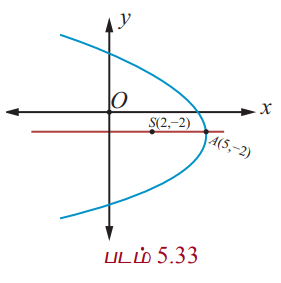
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«ЕЯ»ѕ A(5, Рѕњ2) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я««Я»Ї S(2, РђЊ2), Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«цЯ»ѓЯ«░Я««Я»Ї AS = a = 3.
Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«џЯ»ЇЯ«џЯ»ђЯ«░Я»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ x Рѕњ Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«цЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ»Ђ.
Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
(y + 2)2 = Рѕњ4(3)(x Рѕњ 5)
РЄњ y2 + 4y + 4 = Рѕњ12x + 60
РЄњ y2 + 4y + 12x Рѕњ 56 = 0 .
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.18
Я««Я»ЂЯ«ЕЯ»ѕ (Рѕњ1, Рѕњ2), Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ yРѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (3, 6) Я«хЯ«┤Я«┐Я«џЯ»ЇЯ«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
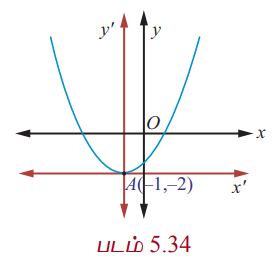
Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ y РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
(x+1)2 = 4a(y + 2).
Я«ЄЯ«цЯ»Ђ (3, 6) Я«хЯ«┤Я«┐Я«џЯ»ЇЯ«џЯ»єЯ«▓Я»ЇЯ«хЯ«цЯ«ЙЯ«▓Я»Ї
(3 + 1)2 = 4a(6 + 2)
РЄњ a = 1/2
Я«јЯ«ЕЯ«хЯ»Є Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (x + 1)2 = 2(y + 2)
Я«ЄЯ«цЯ»ѕЯ«џЯ»ЇЯ«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ x2 + 2x Рѕњ 2y Рѕњ 3 = 0 Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.19
x2 Рѕњ 4x Рѕњ 5y РђЊ 1 = 0. Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЕЯ»ѕ, Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я««Я»Ї, Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«▓, Я«еЯ»ђЯ«│Я««Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
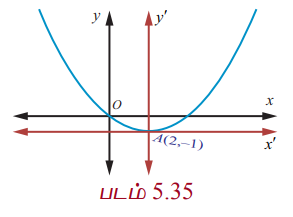
Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
x2 Рѕњ 4x Рѕњ 5y Рѕњ 1 = 0
РЄњ x2 Рѕњ 4x = 5y + 1
РЄњ x2 Рѕњ 4x + 4 = 5y + 1 + 4.
(x Рѕњ 2)2 = 5 (y + 1) Я«ЄЯ«цЯ»Ђ Я«цЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, 4a = 5 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЕЯ»ѕ (2, Рѕњ1), Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я««Я»Ї (2, ┬╝).
Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
y РђЊ k + a = 0
y + 1 + 5/4 = 0
4y + 9 = 0.
Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«▓Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 5 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.20
Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (┬▒2, 0), Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї (┬▒3, 0) Я«ЅЯ«ЪЯ»ѕЯ«» Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
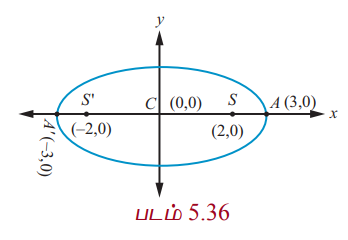
Я«фЯ«ЪЯ««Я»Ї 5.36Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ
SS' = 2c Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 2c = 4 ; A'A = 2a = 6
РЄњ c = 2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a = 3,
РЄњ b2 = a2 Рѕњ c2 = 9 РђЊ 4 = 5.
Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ»Ђ x РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»Ђ, a > b.
Я««Я»ѕЯ«»Я««Я»Ї (0, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я««Я»Ї (┬▒2, 0).
Я«јЯ«ЕЯ«хЯ»Є Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
x2/9 + y2/5 = 1.
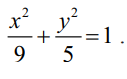
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.21
Я««Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕЯ«цЯ»ЇЯ«цЯ«ЋЯ«хЯ»Ђ ┬й, Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ (2, 3) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я»ѕ x = 7 Я«ЅЯ«ЪЯ»ѕЯ«» Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ»Ђ, Я«ЋЯ»ЂЯ«▒Я»ЇЯ«▒Я«џЯ»ЇЯ«џЯ»Ђ Я«еЯ»ђЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ SP/PM = e Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ SP2 = e2PM2
Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї, (x Рѕњ 2)2 + ( y Рѕњ 3)2 = 1/4(x Рѕњ 7)2
РЄњ 3x2 + 4y2 Рѕњ 2x Рѕњ 24y + 3 = 0, Я«ЄЯ«цЯ»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї
РЄњ 3(x РђЊ 1/3)2 + 4(y Рѕњ 3)2 = 3(1/9) + 4 ├Ќ 9 Рѕњ 3 = 100/3
РЄњ 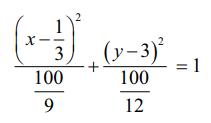 Я«ЄЯ«цЯ»Ђ Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«цЯ»Ђ Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї = 2a = 2Рѕџ(100/9) = 20/3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
Я«ЋЯ»ЂЯ«▒Я»ЇЯ«▒Я«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї= 2b = 2Рѕџ(100/12) =10/Рѕџ3.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.22
4x2 + 36y2 + 40x Рѕњ 288y + 532 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ»Ђ, Я«ЋЯ»ЂЯ«▒Я»ЇЯ«▒Я«џЯ»ЇЯ«џЯ»Ђ Я«еЯ»ђЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я««Я»ЂЯ«┤Я»ЂЯ«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«ЋЯ»ЇЯ«Ћ 4x2 + 36y2 + 40x Рѕњ 288y + 532 = 0,
4(x2 + 10x + 25 Рѕњ 25) + 36(y2 Рѕњ 8y + 16 Рѕњ 16) + 532 = 0 Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ
4(x2 + 10x + 25) + 36(y2 Рѕњ 8y + 16) = Рѕњ532 + 100 + 576
4(x + 5)2 + 36( y Рѕњ 4)2 = 144.
Я«ЄЯ«░Я»ЂЯ«фЯ»ЂЯ«▒Я««Я»ЂЯ««Я»Ї 144РѕњЯ«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
(x + 5)2/36 + (y Рѕњ 4)2/4 = 1.
Я«ЄЯ«цЯ»Ђ Я««Я»ѕЯ«»Я««Я»Ї (РђЊ5, 4), Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ»Ђ xРѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я«ЁЯ«░Я»ѕ Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 12 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ЇЯ«▒Я«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 4. Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї (1, 4) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (Рѕњ11, 4).
Я«цЯ«▒Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, c2 = a2 Рѕњ b2 = 36 РђЊ 4 = 32
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c = ┬▒4Рѕџ2.
Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Рѕњ5 Рѕњ4Рѕџ2, 4) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (Рѕњ5 + 4Рѕџ2, 4) .
Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї = 2a = 12 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
Я«ЋЯ»ЂЯ«▒Я»ЇЯ«▒Я«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї = 2b = 4 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.23
4x2 + y2 + 24x Рѕњ 2y + 21 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я««Я»Ї, Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«▓ Я«еЯ»ђЯ«│Я««Я»Ї 2 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«јЯ«┤Я»ЂЯ«ц Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
4x2 + 24x + y2 Рѕњ 2y + 21= 0
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, 4(x2 + 6x + 9 Рѕњ 9) + (y2 Рѕњ 2y + 1 Рѕњ 1) + 21 = 0
4(x + 3)2 РђЊ 36 + (y Рѕњ 1)2 РђЊ 1 + 21 = 0,
4(x + 3)2 + (y Рѕњ 1)2 = 16,
[ (x + 3)2 /4 ] + [ (y Рѕњ 1)2/16 ] = 1.
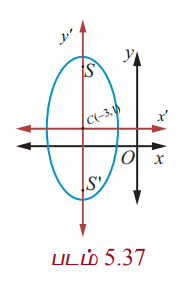
Я««Я»ѕЯ«»Я««Я»Ї (Рѕњ3, 1) a = 4, b = 2, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ»Ђ y РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕ
c2 = 16 РђЊ 4 = 12
c = ┬▒ 2Рѕџ3.
Я«јЯ«ЕЯ«хЯ»Є Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Рѕњ3, 2Рѕџ3 + 1) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (Рѕњ3, Рѕњ2Рѕџ3 + 1).
Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї (3, ┬▒ 4 + 1), Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ (Рѕњ3, 5) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (Рѕњ3, Рѕњ3), Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«▓ Я«еЯ»ђЯ«│Я««Я»Ї = 2b2/a = 2 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї. (Я«фЯ«ЪЯ««Я»Ї 5.37)
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.24
Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї (0, ┬▒4) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (0, ┬▒6) Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
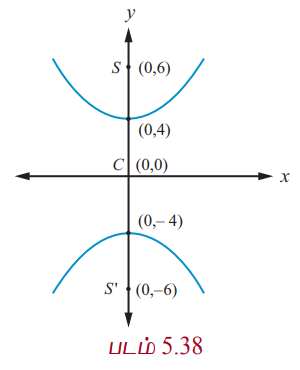
Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я««Я»ѕЯ«»Я««Я»Ї C (0, 0) (Я«фЯ«ЪЯ««Я»Ї 5.38)
Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»ЇЯ«џЯ»Ђ y РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»Ђ
AA' = 2a РЄњ 2a = 8,
SS' = 2c = 12, c = 6
a = 4
b2 = c2 Рѕњ a2 = 36 РђЊ 16 = 20.
Я«јЯ«ЕЯ«хЯ»Є Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ y2/16 Рѕњ x2/20 = 1
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.25
9x2 Рѕњ16y2 = 144 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї, Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
9x2 Рѕњ16y2 = 144 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«цЯ»Ї Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я««Я«ЙЯ«▒Я»ЇЯ«▒
x2/16 Рѕњ y2/9 = 1 Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»ЇЯ«џЯ»Ђ xРѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ»Ђ, Я««Я»ЂЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї (Рѕњ4, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (4, 0);
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c2 = a2 + b2 = 16 + 9 = 25, c = 5.
Я«јЯ«ЕЯ«хЯ»Є Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Рѕњ5, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (5, 0).
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.26
11x2 Рѕњ 25y2 Рѕњ 44x + 50y РђЊ 256 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я««Я»Ї, Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ѕЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«цЯ»ЇЯ«цЯ«ЋЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«хЯ«ЪЯ«┐Я«хЯ««Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒
11(x2 Рѕњ 4x) Рѕњ 25(y2 Рѕњ 2y) Рѕњ 256 = 0
11(x Рѕњ 2)2 Рѕњ 25 (y Рѕњ 1)2 = 256 РђЊ 44 + 25
11(x Рѕњ 2)2 Рѕњ 25(y Рѕњ 1)2 = 275
[ (x Рѕњ 2)2 /25 ] РђЊ [ (y Рѕњ 1)2/11 ] = 1
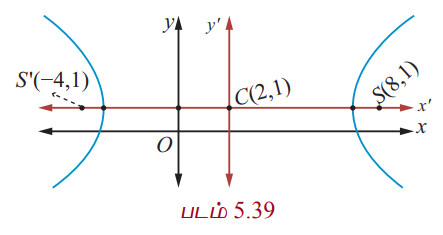
Я««Я»ѕЯ«»Я««Я»Ї (2, 1),
a2 = 25, b2 = 11
c2 = a2 + b2
= 25 + 11 = 36
c = ┬▒ 6
Я«јЯ«ЕЯ«хЯ»Є,
e = c/a = 6/5 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«хЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (8, 1) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (Рѕњ4, 1) (Я«фЯ«ЪЯ««Я»Ї 5.39).
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.27
Я«╣Я«ЙЯ«▓Я»ЄЯ«»Я«┐Я«ЕЯ»Ї Я«хЯ«ЙЯ«▓Я»Ї Я«еЯ«ЪЯ»ЇЯ«џЯ«цЯ»ЇЯ«цЯ«┐Я«░ Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕ, (Я«фЯ«ЪЯ««Я»Ї 5.51) 36.18 Я«хЯ«┐Я«БЯ»ЇЯ«хЯ»єЯ«│Я«┐ Я«ЁЯ«▓Я«ЋЯ»Ђ Я«еЯ»ђЯ«│Я««Я»ЂЯ««Я»Ї 9.12 Я«хЯ«┐Я«БЯ»ЇЯ«хЯ»єЯ«│Я«┐ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ«ЋЯ«▓Я««Я»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕЯ«цЯ»ЇЯ«цЯ«ЋЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
2a = 36.18, 2b = 9.12, Я«јЯ«ЕЯ«цЯ»ЇЯ«цЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
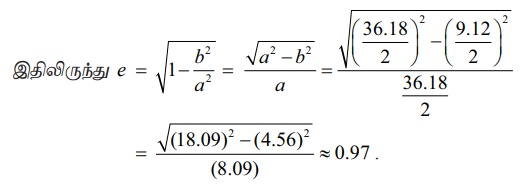
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«њЯ«░Я»Ђ Я«хЯ«┐Я«БЯ»ЇЯ«хЯ»єЯ«│Я«┐ Я«ЁЯ«▓Я«ЋЯ»Ђ (Я«џЯ»ѓЯ«░Я«┐Я«»Я«ЕЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ѓЯ««Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 1,49,597,870 Я«ЋЯ«┐.Я««Я»ђ, Я«фЯ»ѓЯ««Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«░Я»ѕЯ«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ»Ђ.