12 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї : Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я««Я»Ї 5 : Я«ЄЯ«░Я»ЂЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«фЯ«ЋЯ»ЂЯ««Я»ЂЯ«▒Я»ѕ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»ЇРѕњII
Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Conic Sections)
Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Conic Sections)
Я«хЯ«│Я»ѕЯ«хЯ«░Я»ѕЯ«ЋЯ«│Я»ѕ Я«цЯ»ђЯ«░Я»ЇЯ««Я«ЙЯ«ЕЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«фЯ«┐Я«░Я«┐Я«хЯ»Ђ 5.3РѕњЯ«ЄЯ«▓Я»Ї Я«хЯ«┐Я«хЯ«░Я«┐Я«цЯ»ЇЯ«ц Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»ЂЯ«ЪЯ«ЕЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я«ЙЯ«Е Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЊЯ«░Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»ѕ Я«њЯ«░Я»Ђ Я«цЯ«│Я«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї, Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї, Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї, Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є Я«ЁЯ«еЯ»ЇЯ«ц Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЂЯ«Ћ Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ«░Я»ѕЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
1. Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ««Я»ЇРђў (Geometric description of conic section)
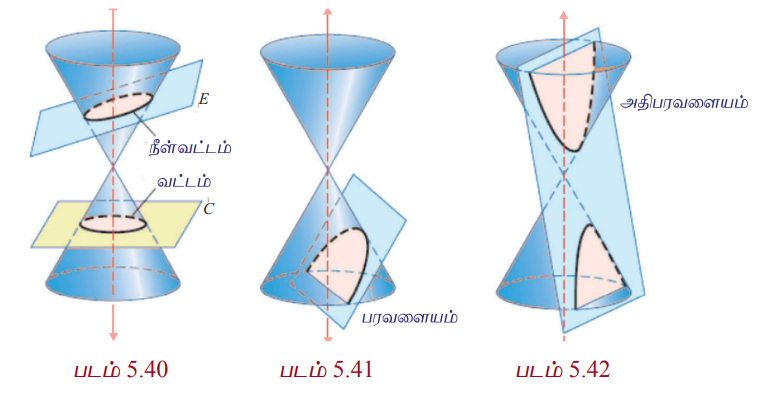
Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Е Я«њЯ«░Я»Ђ Я«цЯ«│Я««Я»Ї (Я«цЯ«│Я««Я»Ї C) Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї (Я«фЯ«ЪЯ««Я»Ї 5.40) Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я«цЯ«│Я««Я»Ї E, Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«џЯ«▒Я»ЇЯ«▒Я»Ђ Я«џЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«ц Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Є Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї (Я«фЯ«ЪЯ««Я»Ї 5.40) Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ Я«њЯ«░Я»Ђ Я«цЯ«│Я««Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї (Я«фЯ«ЪЯ««Я»Ї 5.41) Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ Я«њЯ«░Я»Ђ Я«цЯ«│Я««Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї (Я«фЯ«ЪЯ««Я»Ї 5.42) Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
2. Я«џЯ«┐Я«цЯ»ѕЯ«еЯ»ЇЯ«ц Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Degenerate Forms)
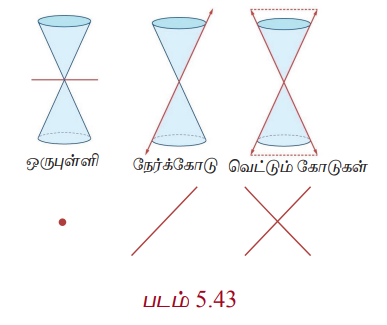
Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«┐Я«цЯ»ѕЯ«еЯ»ЇЯ«ц Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, (Я«фЯ«ЪЯ««Я»Ї 5.43) Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»ѕ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ»Ђ Я««Я»ЂЯ«ЕЯ»ѕ Я«хЯ«┤Я«┐Я«џЯ»ЇЯ«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ«Й Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ, Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐, Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ, Я«ЊЯ«░Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ, Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«БЯ««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«цЯ«│Я««Я»Ї Я«ЅЯ«░Я»ЂЯ«│Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«џЯ«┐Я«цЯ»ѕЯ«хЯ»Ђ Я«њЯ«░Я»Ђ Я«ЅЯ«░Я»ЂЯ«│Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ«┐Я«ЕЯ»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒ Я«цЯ«│Я««Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЕЯ»ѕ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒ Я«цЯ«│Я««Я»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«њЯ«░Я»Ђ Я«џЯ»ІЯ«ЪЯ«┐ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ»Ђ Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«џЯ«┐Я«цЯ»ѕЯ«еЯ»ЇЯ«ц Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї A = B = C = 0 Я«јЯ«ЕЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒ Я«цЯ«│Я««Я»Ї Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЕЯ»ѕ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«џЯ«┐Я«цЯ»ѕЯ«еЯ»ЇЯ«ц Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«░Я»ѕ
Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї (0 < e < 1) Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ«хЯ«░Я»ѕ e = Рѕџ[1 РђЊ b2/a2] , e Рєњ 0 Я«јЯ«ЕЯ«┐Я«▓Я»Ї b/a Рєњ 1 Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ b Рєњ a Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«еЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«џЯ»ЇЯ«џЯ»Ђ, Я«ЋЯ»ЂЯ«▒Я»ЇЯ«▒Я«џЯ»ЇЯ«џЯ»Ђ Я«еЯ»ђЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. e Рєњ 1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї b/a Рєњ 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«цЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«░Я»ѕ
Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»ѕ (e > 1) Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ«хЯ«░Я»ѕ e = Рѕџ[1 + b2/a2], e Рєњ 1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї b/a Рєњ 0 Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ e Рєњ 1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї bРѕњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ aРѕњЯ«љЯ«фЯ»Ї Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ«хЯ«░Я»ѕ Я««Я«┐Я«ЋЯ«џЯ»ЇЯ«џЯ«┐Я«▒Я«┐Я«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«░Я»ЇЯ««Я»ЂЯ«ЕЯ»ѕЯ«»Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї. e Рєњ Рѕъ Я«јЯ«ЕЯ«┐Я«▓Я»Ї a РѕњЯ«љЯ«фЯ»Ї Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ b Я««Я«┐Я«ЋЯ«фЯ»ЇЯ«фЯ»єЯ«░Я«┐Я«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«цЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«»Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї.
3. Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 РѕњЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»ЂЯ«хЯ«│Я»ѕЯ«хЯ«┐Я«ЕЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ѕЯ«»Я«ЙЯ«│Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я»Ї (Identifying the conics from the general equation of the conic Ax2 + Bxy + Cy2 + Dx + Ey + F = 0)
Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ««Я»ЇЯ«фЯ«ЪЯ«┐ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ««Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЈЯ«▒Я»ЇЯ«ф Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї, Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї, Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї, Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї, Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐, Я«хЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«БЯ««Я»Ї, Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
(1) A = C = 1, B = 0, D = Рѕњ2h, E = Рѕњ2k, F = h2 + k2 Рѕњ r2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»ЇЯ«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (x Рѕњ h)2 + (y РђЊ k)2 = r2 Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(2) B = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї A Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ C = 0 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»ЇЯ«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«еЯ«ЙЯ««Я»Ї Я«фЯ«ЪЯ«┐Я«цЯ»ЇЯ«ц Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(3) A РЅа C Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Є Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ««Я»Ї.
(4) A = C Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЁЯ«цЯ«┐Я«фЯ«░Я«хЯ«│Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»ѕЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ««Я»Ї.
(5) A = C Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B = D = E = F = 0, Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ x2 + y2 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї.
(6) A = C = F Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B = D = E = 0, Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ x2 + y2 + 1 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»Ї Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ««Я»Ї.
(7) A РЅа 0 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ C РЅа 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒ Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«єЯ«» Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ««Я»Ї.
(8) A = РѕњC Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ x2 Рѕњ y2 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.28
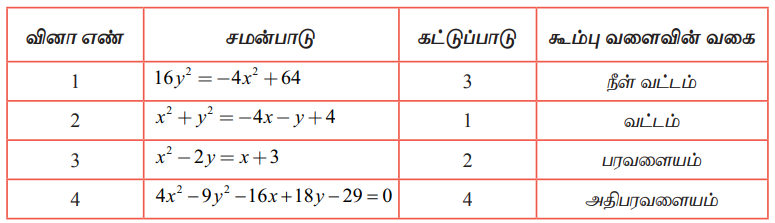
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ѓЯ««Я»ЇЯ«фЯ»Ђ Я«хЯ«│Я»ѕЯ«хЯ«┐Я«ЕЯ»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«Ћ:
(1) 16y2 = Рѕњ4x2 + 64
(2) x2 + y2 = Рѕњ4x РђЊ y + 4
(3) x2 Рѕњ 2y = x + 3
(4) 4x2 Рѕњ 9y2 Рѕњ 16x + 18y Рѕњ 29 = 0
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ