கூம்பு வளைவரையின் தொடுகோடுகள் மற்றும் செங்கோடுகள் (Tangents and Normals to Conics)

கூம்பு வளைவரையின் தொடுகோடுகள் மற்றும் செங்கோடுகள் (Tangents and Normals to Conics)

தொடுகோடு என்பது வளைவரையை ஒரே ஒரு புள்ளியில் தொட்டுச் செல்லும் ஒரு நேர்க்கோடு மற்றும் தொடுகோட்டிற்குச் செங்குத்தாக தொடுபுள்ளி வழியாக செல்லும் நேர்க்கோடு செங்கோடு எனப்படும்.

1. y2 = 4ax என்ற பரவளையத்தின் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகள் (Equation of tangent and normal to the parabola y2 = 4ax)

(i) தொடுகோட்டுச் சமன்பாட்டின் கார்ட்டீசியன் வடிவம் (Equation of tangent in cartesian form)

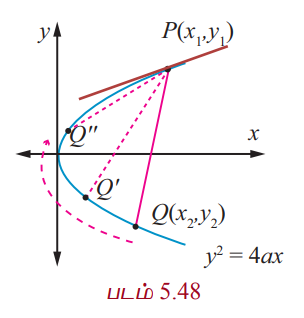
P (x1,  y1)  மற்றும் Q (x2,  y2)  என்ற புள்ளிகள் பரவளையம் y2 = 4ax −ன் மீது உள்ளன என்க.

இதனால், y12 = 4ax1, y22 = 4ax2,

மற்றும் y12 − y22 = 4a(x1 – x2) .

சுருக்க  (y1 – y2)/ (x1 – x2) = 4a/(y1 + y2) , இது நாண் PQ −ன் சாய்வு.

இதனால் 

(y – y1) = [4a/(y1 + y2)] (x – x1) , என்பது நாண் PQ −ன் சமன்பாட்டைக் குறிக்கின்றது.

Q → P அல்லது y2 → y1 எனும்போது நாண் PQ என்பது P −ன் தொடுகோடாக மாறுகின்றது. இதனால் (x1,  y1) −இல் தொடுகோட்டுச் சமன்பாடு

y – y1 = [ 4a /2y1 ] (x – x1) இங்கு 2a/y1 என்பது தொடுகோட்டின் சாய்வு  …. (1)

yy1 − y12 = 2ax − 2ax1

yy1 − 4ax1 = 2ax −2ax1

yy1 = 2a (x + x1)

(ii) தொடுகோட்டுச் சமன்பாட்டின் துணையலகு வடிவம் (Equation of tangent in parametric form) 

பரவளையத்தின் புள்ளி (at2, 2at)−இல் தொடுகோட்டுச் சமன்பாடு

y(2at) = 2a(x+at2)

yt = x + at2

(iii) செங்கோட்டுச் சமன்பாட்டின் கார்ட்டீசியன் வடிவம் (Equation of normal in cartesian form)

(1)−இலிருந்து செங்கோட்டின் சாய்வு − y1/2a

அதனால் செங்கோட்டுச் சமன்பாடு

(y – y1) = [y1/2a] (x – x1)

2ay − 2ay1 = −y1x + y1x1

xy1 + 2ay = y1 (x1 + 2a)

xy1 + 2ay = x1 y1 + 2ay1

(iv) செங்கோட்டுச் சமன்பாட்டின் துணையலகு வடிவம் (Equation of normal in parametric form) 

பரவளையத்தின் புள்ளி (at2,2at) −இல் செங்கோட்டுச் சமன்பாடு

x2at + 2ay = at2 (2at) + 2a(2at)

2a(xt + y) = 2a(at3 + 2at)

y + xt = at3 + 2at

தேற்றம் 5.6

கொடுக்கப்பட்ட புள்ளியிலிருந்து y2 = 4ax என்ற பரவளையத்திற்கு மூன்று செங்கோடுகள் வரையலாம். அவற்றில் ஒன்று எப்போதும் மெய்யானது.

நிரூபணம்

கொடுக்கப்பட்ட பரவளையம் y2 = 4ax மற்றும் (α, β) கொடுக்கப்பட்ட புள்ளி என்க. செங்கோட்டுச் சமன்பாட்டின் துணையலகு வடிவம்

y = −tx + 2at + at3            ……(1)

செங்கோட்டின் சாய்வு m எனில் m = −t

எனவே சமன்பாடு (1)  y = mx − 2am – am3 என மாறுகின்றது

இது (α, β) வழிச் செல்வதால் β = mα − 2am − am3

am3 + (2a − α)m + β = 0

இது m –இல் அமைந்த ஒரு மூன்றாம்படிச் சமன்பாடு. இதற்கு மூன்று m −ன் மதிப்புகள் இருக்கும். இதன் விளைவாக ஒரு புள்ளியிலிருந்து பரவளையத்திற்கு மூன்று செங்கோடுகள் வரையலாம், மெய்யெண் சமன்பாட்டின் கலப்பு எண் மூலங்கள் எப்போதும் இணை எண் கொண்ட சோடியாக அமையும் என்பதாலும் சமன்பாடு (1) ஒற்றைப்படை அடுக்கு கொண்டிருப்பதாலும், குறைந்தபட்சம் ஒரு மெய்யெண் மூலம் இருக்கும். எனவே பரவளையத்தின் செங்கோடுகளில் ஒன்று மெய்யானதாக இருக்கும்.

2. நீள்வட்டம் மற்றும் அதிபரவளையங்களின் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகள் (பின்வரும் நிரூபணங்கள் படிப்பவரின் பயிற்சிக்கு விடப்படுகின்றது) (Equations of tangent and normal to Ellipse and Hyperbola)

3. நேர்க்கோடு y = mx + c கூம்பு வெட்டுமுக வளைவரைகளின் தொடுகோடாக இருக்க நிபந்தனை (Condition for the line y = mx + c to be a tangent to the conic sections)

(i) பரவளையம் y2 = 4ax (Parabola y2 = 4ax)

y2 = 4ax என்ற பரவளையத்தின் மீதுள்ள புள்ளி (x1,  y1) . என்க. எனவே, y12 = 4ax1 …..(1)

பரவளையத்தின் தொடுகோடு y = mx + c என்க.   …..(2)

(x1,  y1) என்ற புள்ளியில் பரவளையத்தின் தொடுகோடு 5.6.1−லிருந்து yy1 = 2a (x + x1) …..(3)

 (2) மற்றும் (3) இரண்டும் ஒரே நேர்க்கோட்டை குறிக்கின்றதால் கெழுக்கள் விகிதச்சமமாக இருக்கும்.

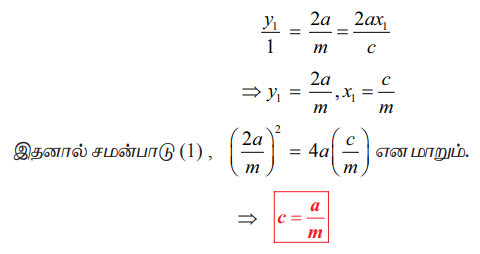
எனவே தொடுபுள்ளி 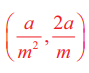மற்றும் பரவளையத்தின் தொடுகோட்டுச் சமன்பாடு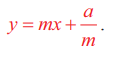

பரவளையத்தைப் போல நீள்வட்டத்திற்கும், அதிபரவளையத்திற்கும் y = mx + c என்ற கோடு தொடுகோடாக இருப்பதற்கான நிபந்தனைகளை நிறுவலாம்.

(ii) நீள்வட்டம் x2/a2 + y2/b2 = 1(ellipse x2/a2 + y2/b2 = 1)

y = mx + c என்ற கோடு நீள்வட்டம் 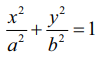  −க்குத் தொடுகோடாக இருக்க நிபந்தனை c2 = a2m2 + b2  தொடுபுள்ளி 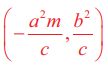மற்றும் தொடுகோட்டுச் சமன்பாடு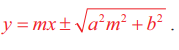

(iii) அதிபரவளையம் x2/a2 − y2/b2 = 1 (Hyperbola x2/a2 − y2/b2 = 1)

y = mx + c என்ற கோடு நீள்வட்டம் 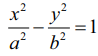−க்குத் தொடுகோடாக இருக்க நிபந்தனை c2 = a2m2 − b2  தொடுபுள்ளி 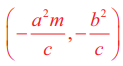மற்றும் தொடுகோட்டுச் சமன்பாடு .

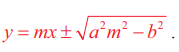குறிப்பு

(1) y = mx ± 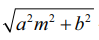  −இல் y = mx + 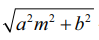அல்லது  y = mx  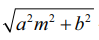−  இவற்றில் ஏதேனும் ஒன்றுதான் நீள்வட்டத்தின் தொடுகோடாக இருக்கும், இரண்டும் அல்ல. 

(2) y = mx ± 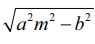  −இல் y = mx + 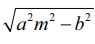அல்லது  y = mx  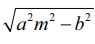−   இவற்றில் ஏதேனும் ஒன்றுதான் அதிபரவளையத்தின் தொடுகோடாக இருக்கும், இரண்டும் அல்ல. 

முடிவுகள்(நிரூபணங்கள் இல்லாமல்)

(1) தளத்தில் உள்ள ஏதேனும் ஒரு புள்ளியிலிருந்து (i) பரவளையம், (ii) நீள்வட்டம், (iii) அதிபரவளையம் ஆகியவற்றுக்கு இரு தொடுகோடுகள் வரையலாம்.

(2) தளத்தில் உள்ள ஏதேனும் ஒரு புள்ளியிலிருந்து (i) நீள்வட்டம், (ii) அதிபரவளையம் ஆகியவற்றுக்கு நான்கு செங்கோடுகள் வரையலாம். 

(3) செங்குத்துத் தொடுகோடுகள் வெட்டிக்கொள்ளும் புள்ளியின் நியமப்பாதை

(i) y2 = 4ax என்ற பரவளையத்திற்கு is x = −a (இயங்குவரை).

(ii) 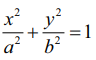என்ற நீள்வட்டத்திற்கு x2 + y2 = a2 + b2 ( இயங்குவட்டம்).

(iii) 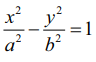  என்ற அதிபரவளையத்திற்கு x2 + y2 = a2 − b2 (இயங்கு வட்டம்) ஆகும்.

எடுத்துக்காட்டு 5.29

x2 + 6x + 4y + 5 = 0 என்ற பரவளையத்திற்கு (1, −3) என்ற புள்ளியில் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளைக் காண்க.

தீர்வு

பரவளையத்தின் சமன்பாடு x2 + 6x + 4y + 5 = 0.

x2 + 6x + 9 – 9 + 4y + 5 = 0

(x + 3)2 = −4(y−1)   ………(1)

X = x + 3, Y = y − 1 எனில்

சமன்பாடு (1) திட்ட வடிவத்தை அடைகிறது.

 X2 = −4Y

தொடுகோட்டின் சமன்பாடு XX1 = −2(Y + Y1)

(1,−3)−இல் X1 = 1 + 3 = 4 ; Y1 = −3 −1 = −4

(1, −3)−இல் தொடுகோட்டின் சமன்பாடு

(x + 3)4 = −2(y – 1 − 4)

2x + 6 = −y + 5 .

2x + y + 1 = 0.

(1, −3)−இல் தொடுகோட்டின் சாய்வு −2, எனவே செங்கோட்டின் சாய்வு 1/2

(1,− 3) −இல் செங்கோட்டின் சமன்பாடு

y + 3 = 1/2(x − 1)

2y + 6 =  x − 1

x − 2y − 7 = 0 .

எடுத்துக்காட்டு 5.30

x2 + 4y2 = 32 என்ற நீள்வட்டத்திற்கு θ = π/4 எனும்போது தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளைக் காண்க.

தீர்வு

நீள்வட்டத்தின் சமன்பாடு

x2 + 4y2 = 32 

x2/32 + y2/8 = 1

a2 = 32, b2 = 8

a = 4√2, b =2√2

θ = π/4 −இல் தொடுகோட்டுச் சமன்பாடு

∴ தொடுகோட்டுச் சமன்பாடு θ = π/4  − இல் என்பதும் புள்ளி (4, 2)−இல் என்பதும் ஒன்றே.

எனவே தொடுகோட்டுச் சமன்பாடு xx1/a2 + yy1/b2 = 1

x + 2y − 8 = 0

தொடுகோட்டுச் சாய்வு −1/2

செங்கோட்டுச் சாய்வு 2

செங்கோட்டின் சமன்பாடு

y − 2 = 2(x − 4)

y − 2x + 6 = 0.