பரவளையம் (Parabola)

2. பரவளையம் (Parabola)

பரவளையத்தின் மையத்தொலைத்தகவு e = 1 என்பதால் ஒரு தளத்தில் குவியம் மற்றும் இயக்குவரைகளுக்கு சமதூரத்தில் இருக்குமாறு நகரும் ஒரு புள்ளியின் நியமப்பாதை பரவளையம் ஆகும்.

(i) முனை (0, 0) உள்ள பரவளைய சமன்பாட்டின் திட்ட வடிவம் (Equation of a parabola in standard form with vertex at (0, 0)

S குவியம் எனவும் l இயக்குவரை எனவும் கொள்க.

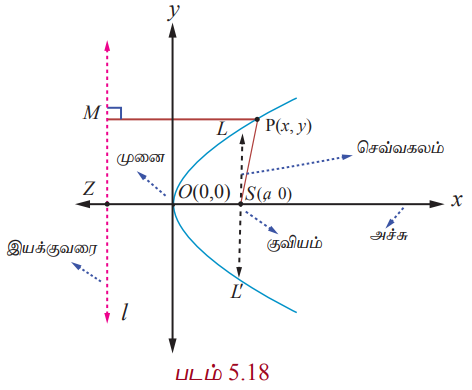
 l −க்கு செங்குத்தாக S வழியே SZ வரைக. SZ – ஐ x −அச்சு எனவும் SZ −ன் மையக்குத்துக்கோட்டை y − அச்சு எனவும் கொள்க. மையக்குத்துக்கோடு SZ−ஐ சந்திக்கும் புள்ளி ஆதிப்புள்ளி O என்க.

SZ = 2a எனில், S என்பது (a, 0) மற்றும் இயக்குவரையின் சமன்பாடு x + a = 0 ஆகும்.

பரவளையத்தை தரும் நகரும் புள்ளி P(x, y) என்க. இயக்குவரைக்கு செங்குத்தாக PM வரைக.

பரவளைய வரையறையின்படி e = SP/PM = 1. அதாவது SP2 = PM2.

எனவே, (x − a)2 + y2 = (x + a)2. இதை விரிவுபடுத்திச் சுருக்க y2 = 4ax எனக் கிடைக்கின்றது. இது பரவளையச் சமன்பாட்டின் திட்ட வடிவமாகும். பரவளையச் சமன்பாட்டின் மற்ற திட்டவடிவங்கள் y2 = −4ax, x2 = 4ay, மற்றும் x2 = −4ay ஆகும்.

வரையறை 5.3

• இயக்குவரைக்கு செங்குத்தாகவும், குவியம் வழியாகவும் செல்லும் நேர்கோடு பரவளையத்தின் அச்சு எனப்படும்.

• பரவளையம் மற்றும் அதன் அச்சு வெட்டிக்கொள்ளும் புள்ளி பரவளையத்தின் முனை எனப்படும்.

• பரவளையத்தின் குவியம் வழியாகச் செல்லும் நாண் அப்பரவளையத்தின் குவி நாண் எனப்படும்.

• பரவளையத்தின் அச்சுக்கு செங்குத்தாக உள்ள குவிநாண் பரவளையத்தின் செவ்வகலம் ஆகும்.

எடுத்துக்காட்டு 5.14

பரவளையம் y2 = 4ax −ன் செவ்வகல நீளம் காண்க.

தீர்வு

பரவளையத்தின் சமன்பாடு y2 = 4ax .

செவ்வகலம் LL' குவியம் (a, 0) வழிச் செல்கின்றது. (படம் 5.18−ஐ பார்க்கவும்)

எனவே L என்பது (a, y1) ஆகும்.

அதனால் y12 = 4a2 .

எனவே y1 =  ± 2a.

செவ்வகலத்தின் முனைப்புள்ளிகள் (a, 2a) மற்றும் (a, −2a) ஆகும்.

எனவே செவ்கலத்தின் நீளம் LL’ = 4a .

குறிப்புரை

பரவளையச் சமன்பாட்டின் திட்ட வடிவம் y2 = 4ax −க்கு முனை (0, 0), அச்சு x−அச்சு மற்றும் குவியம் (a, 0) ஆக இருக்கும். பரவளையம் y2 = 4ax முழுவதுமாக .x −அச்சின் குறையற்ற பகுதியில் அமையும். y2 = 4ax −இல் y−க்கு −y பிரதியிட சமன்பாடு மாறாமல் இருக்கின்றது. எனவே பரவளையம் y2 = 4ax, x −அச்சுக்கு சமச்சீராக இருக்கும். அதாவது y2 = 4ax பரவளைத்தின் சமச்சீர் அச்சு x−அச்சாகும்.

(ii) (h,k)−ஐ முனையாக உடைய பரவளையங்கள் (Parabolas with vertex at (h,k))

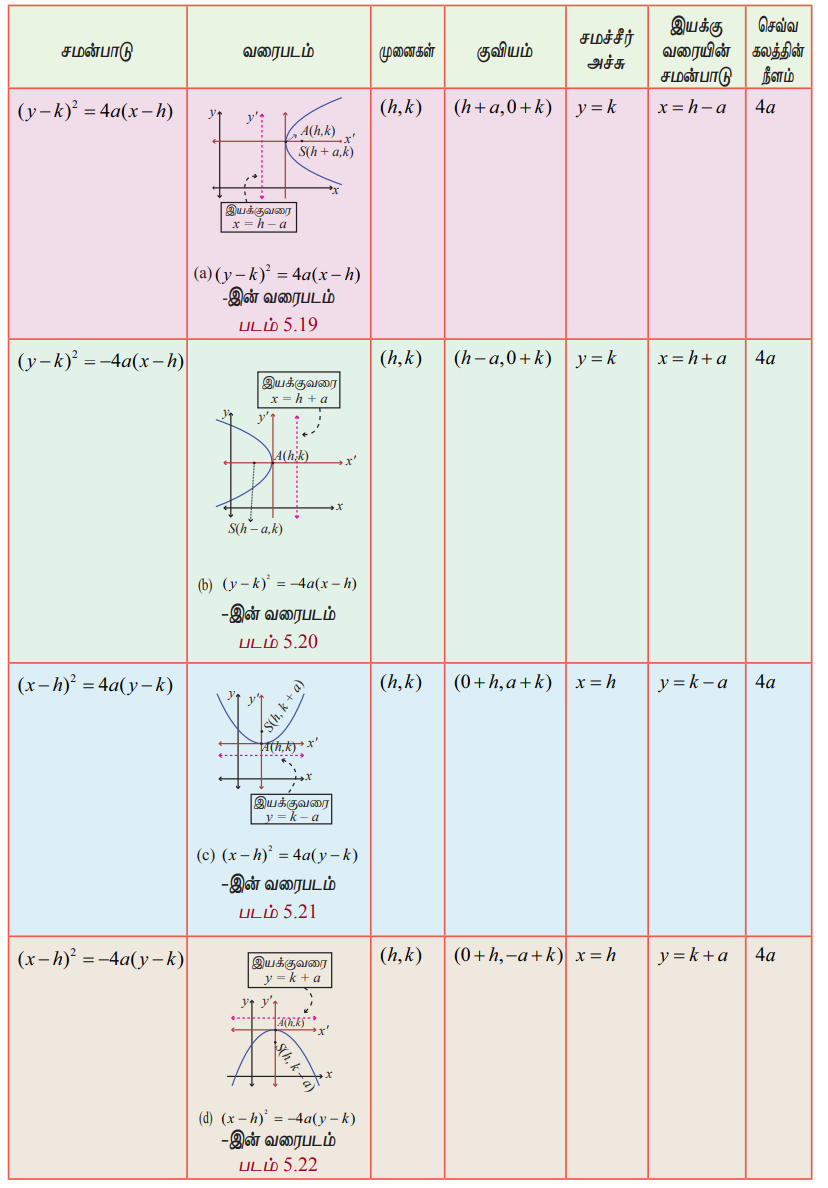
முனை (h,k) மற்றும் அச்சு x−அச்சுக்கு இணை எனில் பரவளையத்தின் சமன்பாடு (y − k)2 = 4a(x − h) அல்லது (y − k)2 = −4a(x − h) என இருக்கும் (படம் 5.19, 5.20).

முனை (h, k) மற்றும் அச்சு y−அச்சுக்கு இணை எனில் பரவளையத்தின் சமன்பாடு (x − h)2 = 4a(y − k) அல்லது (x − h)2 = −4a(y − k) (படம் 5.21, 5.22).