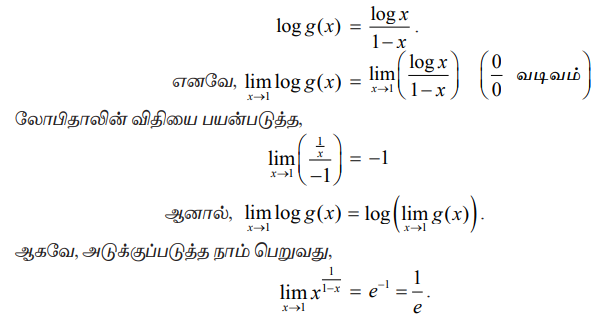தேரப்பெறா வடிவங்கள் (Indeterminate Forms)

தேரப்பெறா வடிவங்கள் (Indeterminate Forms)

இப்பாடப்பகுதியில் எல்லை மதிப்பினை காணும்பொழுது தேரப்பெறா வடிவங்கள் வரும் நிலையில் எவ்வாறு எல்லை மதிப்பினைக் கணக்கிடுவது என்பதைப் பற்றி காண்போம். 

எல்லை காணும் முறை (A Limit Process)

R(x) எனும் ஒரு சார்பிற்கு limx→a R(x) எனும் எல்லையை காணும்பொழுது நாம்

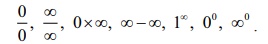
0/0,∞/∞,0 × ∞, ∞-∞,1∞.00, ∞0ஆகிய சூழ்நிலைகளை சந்திக்க நேரலாம்.

இம்மாதிரியான வடிவங்களில் உள்ள எண்களை, நாம் சாதாரணமான கூட்டல் மற்றும் பெருக்கலின் விதிகளைக் கொண்டு மதிப்பிட முடியாது. இம்மாதிரியான வடிவங்களை நாம் தேரப்பெறா வடிவங்கள் என்கிறோம். இவ்வடிவங்களை ஒரு எண்ணாக கருத முடியாது என்றபோதிலும், இந்த தேரப்பெறா வடிவங்களின் எல்லை மதிப்புகள் ஒரு முக்கிய பங்கினை வகிக்கிறது.

ஜான் பெர்னோலி என்பவர் தொகுதி மற்றும் பகுதி ஆகியவை இரண்டும் பூச்சியத்தையோ அல்லது ∞-யையோ நெருங்கும்போது வகைக்கெழுக்களை கொண்டு எவ்வாறு எல்லை மதிப்பை காண்பது எனும் முறையை கண்டுபிடித்தார். இந்த விதியை தற்போது லோபிதாலின் விதி என்று அழைக்கிறோம். இவ்விதியானது குய்லூம் டி லோபிதால் என்ற பிரெஞ்சு அறிஞர் எழுதிய வகை நுண்கணிதத்தின் அறிமுகம் (Introductory Differential Calculus) எனும் நூலில்தான் முதன் முதலில் அச்சிடப்பட்டது. அதனாலேயே இவ்விதியை லோபிதாலின் விதி என்று அழைக்கிறோம்.

லோபிதாலின் விதி (The I'Hopital's Rule)

f (x) மற்றும் g(x) ஆகியவை வகையிடத்தக்க சார்புகள் மற்றும் g'(x) ≠ 0 மேலும்

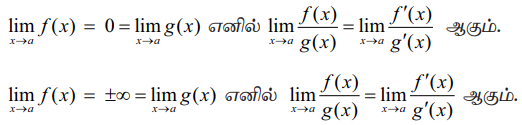
தேரப்பெறா வடிவங்கள் (Indeterminate forms) 0/0, ∞/∞, 0×∞, ∞ - ∞

எடுத்துக்காட்டு 7.33

கணக்கிடுக : limx→1 ( x2 - 3x + 2 /  x2 - 4x + 3)

தீர்வு

x = 1 என நேரடியாக பிரதியிடும்போது நாம் 0/0 என்ற தேரப்பெறா வடிவத்தைப் பெறுகிறோம்.

தொகுதி மற்றும் பகுதி ஆகியவை வரிசை 2 உள்ள பல்லுறுப்புக் கோவை. ஆகவே எனவே வகையிடத்தக்கவை. ஆகவே, லோபிதாலின் தேற்றத்தைப் பயன்படுத்த,

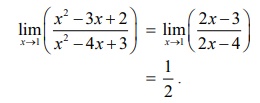
எல்லை மதிப்பை 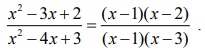என காரணிப்படுத்தல் முறையிலும் காணலாம்.

எடுத்துக்காட்டு 7.34

கணக்கிடுக : lim x→a (xn – an / x-a)

தீர்வு

x = a என நேரடியாக பிரதியிடும்போது நாம் 0/0 என்ற தேரப்பெறா வடிவத்தைப் பெறுகிறோம். தொகுதி மற்றும் பகுதி ஆகியவை பல்லுறுப்புக் கோவைகள். ஆதலால் வகையிடத்தக்கவை. எனவே, லோபிதாலின் தேற்றத்தைப் பயன்படுத்த,

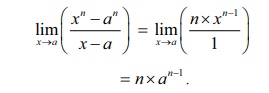
எடுத்துக்காட்டு 7.35

மதிப்பு காண்க :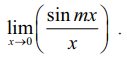

தீர்வு

x = 0 என நேரடியாக பிரதியிடும்போது நாம் 0/0 என்ற தேரப்பெறா வடிவத்தைப் பெறுகிறோம்.ஆகவே, லோபிதாலின் தேற்றத்தைப் பயன்படுத்த,

அடுத்த எடுத்துக்காட்டில் எல்லை இல்லாத் தன்மையை அறியலாம். 

எடுத்துக்காட்டு 7.36 

மதிப்பு காண்க :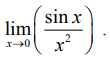

தீர்வு

x = 0 என நேரடியாக பிரதியிடும்போது நாம் 0/0 என்ற தேரப்பெறா வடிவத்தைப் பெறுகிறோம். ஆகவே, லோபிதாலின் தேற்றத்தைப் பயன்படுத்த,

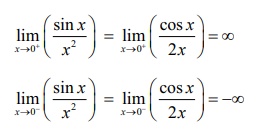
இடது மற்றும் வலது எல்லைகள் சமமில்லை ஆதலால் எல்லை இல்லை.

குறிப்புரை

lim x→10+(cos x / 2x)-க்கு ஒருவர் மீண்டும் லோபிதாலின் விதியைப் பயன்படுத்தி

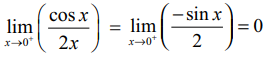 எனக் காண்பது சரியானது அல்ல

ஏன் எனில் 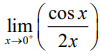என்பது தேரப்பெறா வடிவத்தில் இல்லை.

எடுத்துக்காட்டு 7.37

தீர்வு

இது (0/0) என்ற தேரப்பெறா வடிவத்தில் உள்ளதால், லோபிதாலின் விதியை பயன்படுத்த,

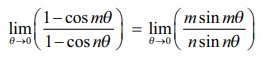
எடுத்துக்காட்டு 7.35-ஐ பயன்படுத்த,

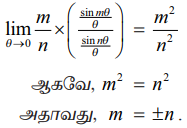
ஆகவே, m2 = n2

அதாவது, m = ± n. 

எடுத்துக்காட்டு 7.38

மதிப்பு காண்க :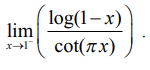

தீர்வு

இது ∞/∞ எனும் தேரப்பெறா வடிவில் உள்ளது. எனவே, எல்லை மதிப்பை காண லோபிதாலின்விதியை நாம் பயன்படுத்தலாம்.

எடுத்துக்காட்டு 7.39

மதிப்பு காண்க :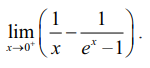

தீர்வு

இது ∞ - ∞ எனும் தேரப்பெறா வடிவில் உள்ளது. எல்லையை மதிப்பிட இதனை (0/0) வடிவத்திற்குமாற்றி, லோபிதாலின் விதியை பயன்படுத்த வேண்டும்.

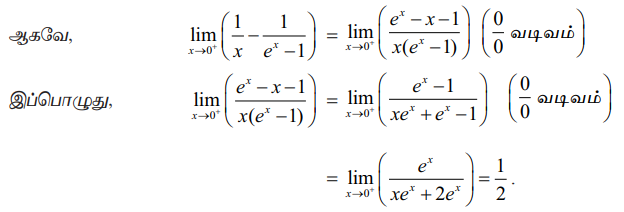
எடுத்துக்காட்டு 7.40

மதிப்பு காண்க :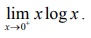  

தீர்வு

இது (0 / ∞) எனும் தேரப்பெறா வடிவில் உள்ளது. எல்லையை மதிப்பிட நாம் இதனை  (∞/∞) எனும் தேரப்பெறா வடிவத்திற்கு மாற்ற வேண்டும். அதன் பிறகு லோபிதாலின் விதியை பயன்படுத்த வேண்டும்.

ஆகவே,

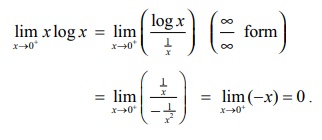
எடுத்துக்காட்டு 7.41

மதிப்பு காண்க :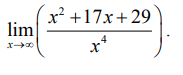

தீர்வு

இது (∞ /∞) எனும் தேரப்பெறா வடிவில் உள்ளது. இந்த எல்லையைக் காண லோபிதாலின் விதியை நாம் பயன்படுத்தலாம்.

ஆகவே,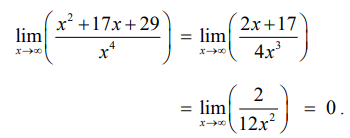

எடுத்துக்காட்டு 7.42

மதிப்பு காண்க :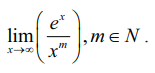

தீர்வு

இது (∞ /∞) எனும் தேரப்பெறா வடிவில் உள்ளது. ஆகவே m முறை லோபிதாலின் விதியை பயன்படுத்த வேண்டும்.

ஆகவே,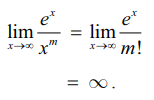

தேரப்பெறா வடிவங்கள் (Indeterminate forms) 0°,1∞ மற்றும் ∞°

இவ்வாறான தேரப்பெறா வடிவங்களை மதிப்பிட, நாம் முதலில் எல்லை மதிப்பிற்கான சேர்ப்பு சார்பு தேற்றத்தை வரையறுப்போம். 

தேற்றம் 7.6

Lim gx→α (x) காணத்தக்கது மற்றும் இதன் மதிப்பு L என்க. மேலும் f (x) ஆனது x = L –ல் தொடர்ச்சியானது என்க. ஆகவே,

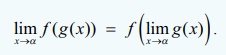
எல்லையை மதிப்பிடும் முறை 

(1) A = limx→α g(x) மடக்கைச் சார்பின் தொடர்ச்சித் தன்மைக்காக A > 0 எனக்கொண்டு,

இருபுறமும் மடக்கை எடுக்க log A = limx→α log(g(x)) எனப்பெறலாம். எனவே f (x) = logx -க்கு மேற்கண்ட தேற்றத்தைப் பயன்படுத்த,

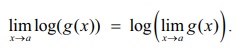
(2) நாம் லோபிதாலின் விதியை பயன்படுத்த, limx→α log(g(x))ஆனது (0/0) அல்லது (∞/∞) வடிவத்தில் இருக்க வேண்டும். 

(3) மதிப்பிடப்பட்ட எல்லை α எனக்கொண்டால் தேவையான எல்லை eα ஆகும். 

எடுத்துக்காட்டு 7.43

லோபிதாலின் விதியை பயன்படுத்தி, limx→0+ (1+ x )1/x = e . என நிறுவுக.

தீர்வு

இது 1∞எனும் தேரப்பெறா வடிவில் உள்ளது. g(x) = (1+x)1/x என்க. மடக்கை எடுக்க,

எடுத்துக்காட்டு 7.44

மதிப்பிடுக :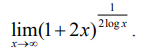 

தீர்வு

இது ∞0 எனும் தேரப்பெறா வடிவில் உள்ளது.

g(x) = (1+ 2x) 1/2log x  என்க.

மடக்கை எடுக்க,

log g(x) = log(1+ 2x) / 2 log x

ஆகவே அடுக்குப்படுத்த, நமக்குத் தேவையான எல்லையினை √e எனப் பெறலாம். 

எடுத்துக்காட்டு 7.45

மதிப்பிடுக :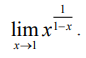 

தீர்வு

x → 1 எனில் 1∞ எனும் தேரப்பெறாத வடிவில் உள்ளது. g(x) = x1/1-x என்க. மடக்கை எடுக்க

Log g(x) = log x / 1- x