சம இறுதிநிலை பயன்பாட்டு விதி

சம இறுதிநிலை பயன்பாட்டு விதி

குறைந்து செல் இறுதிநிலைப் பயன்பாட்டு விதி ஒற்றைப் பண்ட நுகர்வு விருப்பத்திற்கு மட்டுமே பொருந்துகிறது. ஆனால் உண்மையில் விருப்பங்கள் எண்ணற்றவை. அவை நிறைவேற்றப்படக் கூடியவை. இவ்வாறு எண்ணற்ற பண்டங்களை நுகரும் சூழலில், குறைந்து செல் இறுதிநிலைப் பயன்பாட்டு விதியானது விரிவாக்கப்பட்டு சம இறுதிநிலை பயன்பாட்டு விதியாக உருவானது. இவ்விதி ‘பதிலீட்டுவிதி' என்றும் அழைக்கப்படுகிறது. மேலும் இவ்விதி "நுகர்வோரின் சமநிலை விதி", "காசனின் இரண்டாம் விதி" மற்றும் "உச்ச பட்ச திருப்தி விதி" என்றும் அழைக்கப்படுகிறது.

வரையறை

மார்ஷலின் கூற்றுப்படி "ஒரு மனிதன் பல வகையிலும் பயன்படுத்தக்கூடிய ஒரு பொருளைப் பெற்றிருந்தால், அதன் பலவகைப் பயன்களிடையே பகிர்ந்தளிக்கும்போது அதன் பயன்களின் இறுதிநிலைப் பயன்பாடு ஒரே அளவில் சமமாய் இருக்கும்படி பகிர்ந்தளிப்பான். ஒன்றை விட மற்றொன்றில் அதிக இறுதிநிலைப் பயன்பாடு கிடைக்குமெனில் அவர் அதிகப்பயன் பெறும் நோக்கில் குறைந்த பயன் தரும் பொருளில் இருந்து அதிக பயன் தரும் பொருளுக்கு மாறிவிடுவார்".

அனுமானங்கள் 

1. திருப்தியை அதிகப்படுத்த விரும்பக்கூடிய பகுத்தறிவாளராக இருக்க வேண்டும். 

2. ஒவ்வொரு பண்டத்தின் பயன்பாடும் எண்ணளவில் அளவிடப்பட வேண்டும். 

3. பணத்தின் இறுதிநிலைப் பயன்பாட்டில் மாற்றமில்லை. 

4. நுகர்வோரின் வருமானம் வரையறுக்கப்பட்டது. 

5. பொருட்களின் சந்தையில் நிறைவுப் போட்டி நிலவுகிறது.

6. பண்டங்களின் விலைகள் வரையறுக்கப்பட்டது. 

7. குறைந்து செல் இறுதிநிலை பயன்பாட்டு விதி செயல்படுகிறது.

விளக்கம்

ஓர் எடுத்துக்காட்டின் மூலம் இவ்விதி விளக்கப்படுகிறது. ஆப்பிள் மற்றும் ஆரஞ்சு என்று இரு பண்டங்களில் தன் வரையறுக்கப்பட்ட வருமானத்தை ஒரு நுகர்வோர் செலவிட விரும்புகிறார் என்று எடுத்துக்கொள்வோம்.  அவரின் வரையறுக்கப்பட்ட வருமானத்தில் அதிக திருப்தியை பெறக்கூடிய நிலையில் அவர் சமநிலையை அடைவார். கீழ்க்கண்டவாறு அவரின் சமநிலையை விளக்கலாம்.

ஆப்பிளின் இறுதிநிலைப் பயன்பாடு/ ஆப்பிளின் விலை

 = ஆரஞ்சின் இறுதிநிலைப் பயன்பாடு / ஆரஞ்சின் விலை = K

எனவே MUA/PA= MUO/Po= K

K - என்பது பணத்தின் நிலையான இறுதிநிலைப் பயன்பாடு 

எ.கா. 50/10= 20/4=5

மேற்கூறிய சமன்பாட்டின் அடிப்படையில் இவ்விதியானது 'நுகர்வுச் சமநிலை விதி' என்று அழைக்கப்படுகிறது.

ஒரு வேளை MUA/PA வைவிட MUO/Po குறைவாக இருக்குமெனில் அவர் ஆப்பிளிலிருந்து ஆரஞ்சுக்குத் தான் செலவழிக்கும் தொகையை மாற்றிக் கொள்வார். இந்த பதிலீட்டு செயலானது அவருக்கு அதிக மனநிறைவை இரண்டு பண்டங்களில் இருந்தும் பெற வழிவகுக்கும். எனவே, இவ்விதியானது 'பதிலீட்டு விதி' என்றும் அழைக்கப்படுகிறது. எ.கா. ஆரஞ்சு : 20/4 ஆப்பிள் 50/25 

இச்சூழலில் ஆப்பிளை நுகர்வதைவிட, ஆரஞ்சை நுகர்வதுதான் புத்திசாலித்தனம்.

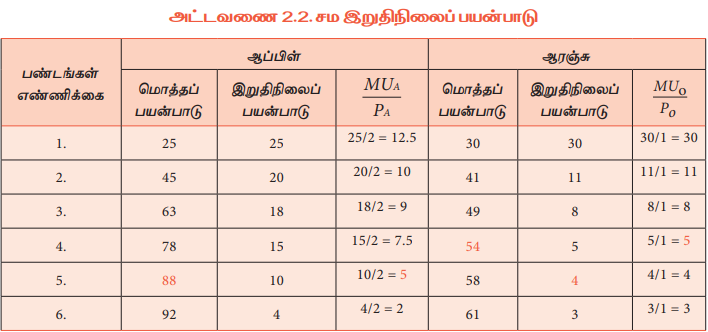
எடுத்துக்காட்டு - விளக்கம்:

அட்டவணை 2.2-ன் உதவியுடன் இவ்விதி விளக்கப்படுகிறது. நுகர்வோர் ₹14 ஐ வருமானமாகக் கொண்டுள்ளார் என எடுத்துக் கொள்வோம். அவர் அந்த முழுத் தொகையையும் ஆப்பிளுக்காகவும் ஆரஞ்சுக்காகவும் செலவிட விரும்புகிறார். ஆப்பிளின் விலை ₹2 ஆரஞ்சின் விலை ₹1 ஆகவும் இருக்கிறது.

நுகர்வோர் உச்ச பயன்பாட்டினை அடைய விரும்பினால் அவர் 5 அலகு ஆப்பிளையும் 4 அலகு ஆரஞ்சையும் வாங்குவார். இதன் மூலம் அவர் 142 அலகுகள் (88+54) மொத்தப் பயன்பாட்டினை பெறுகிறார். 

இங்கு, MUA/PA= MUO/Po, எனவே 10/2 = 5/1

A2A3 மற்றும் B2B3 கோடுகள் விளக்கத்திற்குப் பயன்படுத்தப்படவில்லை

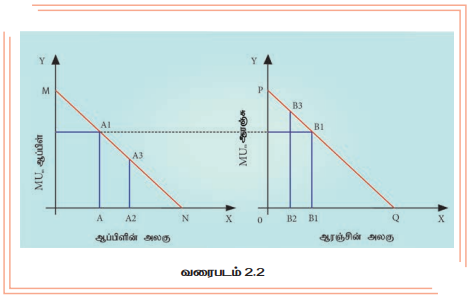
வரைபட விளக்கம் 

வரைபடம் 2.2ல் x அச்சில் செலவின் அளவும், Y அச்சில் ஆப்பிள் மற்றும் ஆரஞ்சின் இறுதிநிலை பயன்பாட்டையும் குறிப்பிடுகிறோம்.

நுகர்வோர் ஆப்பிளுக்காக ₹10ம், ஆரஞ்சுக்காக ₹4ம் செலவிடுகிறார் எனக் கொண்டால், இரண்டின் இறுதி நிலைப் பயன்பாடும் சமமாக இருக்கும். [i.e. AA1 = BB1 (5=5)]. ஆகவே, அவர் உச்ச பயன்பாட்டினை பெறுகிறார்.

குறைபாடுகள்

1. பயன்பாட்டினை அளவிட முடியாது, உணர மட்டுமே முடியும்.