இயற்கணிதம் | அலகு 3 | 8 ஆம் வகுப்பு கணக்கு - முற்றொருமைகள் | 8th Maths : Chapter 3 : Algebra
8 ஆம் வகுப்பு கணக்கு : அலகு 3 : இயற்கணிதம்
முற்றொருமைகள்
முற்றொருமைகள்
நாம் சென்ற வகுப்பில் அடிப்படை இயற்கணித முற்றொருமைகள் பற்றி படித்துள்ளோம். இயற்கணித முற்றொருமை என்பது ஒரு சமன்பாடு ஆகும். அதில் உள்ள மாறிகள் எந்த ஒரு மதிப்புக்கும் அச்சமன்பாட்டை நிறைவு செய்யும், இப்போது நாம் சென்ற வகுப்பில் படித்த நான்கு முற்றொருமைகளை நினைவு கூர்வோம். அவை
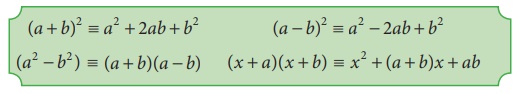
(a + b)2 ≡ a2 + 2ab + b2
(a – b) 2 ≡ a2 – 2ab + b2
(a2 – b2) ≡ (a + b)(a – b)
(x + a) (x + b) ≡ x2 + (a + b)x + ab
குழப்பங்களை தவிர்க்க சர்வசம குறியீட்டுக்கு (≡) பதிலாக சமக்குறியீடு (=) ஆலும் முற்றொருமைகள் குறிக்கப்படுகிறது
இவற்றை முயல்க
பின்வருவனவற்றை விரிவாக்குக.
(i) (p + 2) 2 = .........................
(ii) (3–a) 2 = ...............
(iii) (62 – x2) = .............
(iv) (a + b)2 – (a – b)2 = ...................
(v) (a + b)2 = (a + b) × .................
(vi) (m+n) (....) = m2 – n2
(vii) (m + ...)2 = m2 +14m + 49
(viii) (k2 – 49) = (k +...) (k – ...)
(ix) m2 – 6m + 9 = .............
(x) (m –10) (m + 5) = ..........
குறிப்பு
7x + 3 = 10 இக்கு x = 1 மட்டுமே ஒரு தீர்வாகும். ஆனால் (x + 2)2 = x2 + 4x + 4. இல் x இன் எந்த மதிப்பும் இதனை நிறைவு செய்யும். எனவே 7x + 3 = 10 என்பது ஒரு சமன்பாடு ஆகும். (x + 2)2 = x2 + 4x + 4 என்பது ஒரு முற்றொருமையாகும். எனவே ஒரு முற்றொருமை என்பது சமன்பாடாகும் ஆனால் அதன் மறுதலை உண்மையல்ல.
1. முற்றொருமைகளின் பயன்பாடு
இயற்கணிதக் கோவைகளின் பெருக்கல் மூலம் தீர்வு காணும் கணக்குகளை இயற்கணித முற்றொருமைகளைப் பயன்படுத்தி மாற்றுமுறையில் தீர்வு காணமுடியும்.
எடுத்துக்காட்டு 3.8
(3a + 4c) 2 இன் மதிப்பை (a + b)2 என்ற முற்றொருமையைப் பயன்படுத்திக் காண்க.
தீர்வு :
(3a + 4c) 2 ஐ (a + b) 2 உடன் ஒப்பிட நமக்கு a = 3a, b = 4c எனக் கிடைக்கிறது
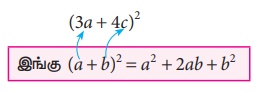
∴ (3a + 4c)2 = (3a) 2 + 2(3a)(4c) + (4c)2 (a, b மதிப்புகளைப் பிரதியிட)
மேலும், = 32a2 + (2 × 3 × 4)(a × c) + 42c2
(3a + 4c) 2 = 9a2 + 24ac + 16c2
எடுத்துக்காட்டு 3.9
9982 ன் மதிப்பை (a – b)2 என்ற முற்றொருமையைப் பயன்படுத்திக் காண்க.
தீர்வு:
998 ஐ (1000 – 2) என எழுத இயலும்.
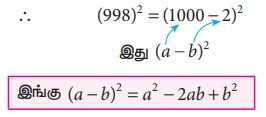 உடன் ஒப்பிட நமக்கு a = 1000, b = 2 எனக் கிடைக்கிறது.
உடன் ஒப்பிட நமக்கு a = 1000, b = 2 எனக் கிடைக்கிறது.
(1000 – 2) 2 = (1000) 2 – 2(1000)(2) + (2) 2
= 1000000 – 4000 + 4
(998) 2 = 996004
சிந்திக்க
(3a) 2 க்கு சமமானது எது?
(i) 3a2
(ii) 32a
(iii) 6a2
(iv) 9a2
எடுத்துக்காட்டு 3.10
(3x + 5y)(3x – 5y) ன் மதிப்பை (a + b) (a – b) என்ற முற்றொருமையைப் பயன்படுத்திக் காண்க.
தீர்வு:
இங்கு, (3x + 5y)(3x – 5y)
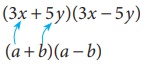
(a + b)(a – b) உடன் ஒப்பிட நமக்கு a = 3x b = 5y எனக் கிடைக்கிறது.
இங்கு (a + b)(a – b) = a2 – b2
(3x + 5y) (3x – 5y) = (3x) 2 – (5y) 2 (a, b மதிப்புகளை பிரதியிட)
= 32 x2 – 52 y2
(3x + 5y) (3x – 5y) = 9x2 – 25y2
எடுத்துக்காட்டு 3.11
y2 – 16 ஐ a2 – b2 என்ற முற்றொருமையைப் பயன்படுத்தி விரிவாக்குக.
தீர்வு:
y2 –16 ஐ y2 – 42 என எழுதலாம்.
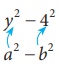
a2 – b2 உடன் ஒப்பிட நமக்கு a = y, b = 4 எனக் கிடைக்கிறது.
இங்கு a2 – b2 = (a + b) (a – b)
y2 – 42 = (y + 4)(y – 4)
y2 – 16 = (y + 4) (y – 4)
எடுத்துக்காட்டு 3.12
(5x + 3) (5x + 4) ஐ (x + a) (x + b) என்ற முற்றொருமையைப் பயன்படுத்திச் சுருக்குக.
தீர்வு:
(5x + 3) (5x + 4) ஐ (x + a) (x + b) உடன் ஒப்பிட, x = 5x மற்றும் a = 3, b = 4 எனக் கிடைக்கிறது
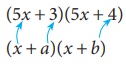
(x + a)(x + b) = x2 + (a + b)x + ab (x, a மற்றும் b ன் மதிப்புகளைப் பிரதியிட)
(5x + 3)(5x + 4) = (5x) 2 + (3 + 4) (5x) + (3) (4)
= 52 x2 + (7)(5x) + 12
(5x + 3) (5x + 4) = 25x2 + 35x + 12
இவற்றை முயல்க
பொருத்தமான முற்றொருமையைப் பயன்படுத்தி விரிவாக்குக.
(i) (3p + 2q) 2
(ii) (105) 2
(iii) (2x – 5d) 2
(iv) (98) 2
(v) (y – 5)( y + 5)
(vi) (3x) 2 – 52
(vii) (2m + n) (2m + p)
(viii) N 203 × 197
(ix) (x – 2) பக்க அளவுள்ள சதுரத்தின் பரப்பளவு காண்க.
(x) நீளம் மற்றும் அகலம் முறையே (y + 4) மற்றும் (y – 3) என கொண்ட செவ்வகத்தின் பரப்பளவைக் காண்க.