நேர்க்கோட்டு வரைபடங்கள்

நேர்க்கோட்டு வரைபடங்கள் 

1. நேர்க்கோட்டு அமைப்பு

(0,2) (1,3) (2,4) (3,5) (4,6). ஆகிய புள்ளிகளை ஆயஅச்சுகள் தளத்தில் குறிக்கவும். நீங்கள் காண்பது என்ன? இவை அனைத்தும் ஒரு நேர்க்கோட்டில் அமைகிறது அல்லவா? அவற்றுள் ஓர் அமைப்பு முறை உள்ளது. ஒவ்வொரு சோடியிலும் உள்ள y ஆயத்தொலைவைக் கவனிக்கவும். 2 = 0 + 2;  3 = 1 + 2; 4 = 2 + 2; 5 = 3 + 2; 6 = 4 + 2 ஒவ்வொரு சோடியிலும், y ஆயத்தொலைவு என்பது x ஆயத்தொலைவைக் காட்டிலும் இரண்டு அதிகம். ஒவ்வொரு புள்ளியின் ஆயத்தொலைவுகளும் இதே தொடர்பைக் கொண்டுள்ளன. அனைத்துப் புள்ளிகளையும் குறிக்க, அவை ஒரு நேர்க்கோட்டில் அமைவதைப் பார்க்கிறோம்.

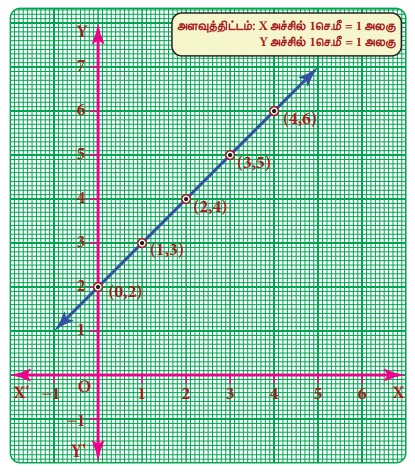
இதுபோன்ற சூழ்நிலைகளில், அனைத்துப் புள்ளிகளையும் வரைபடத்தாளில் குறித்து, அவை ஒரே நேர்க்கோட்டில் அமைந்தால் 'நேர்க்கோட்டு அமைப்பு' எனக் கூறுகின்றோம்.

இந்த எடுத்துக்காட்டில் ஒவ்வொரு வரிசைச்சோடியிலும் y இன் மதிப்பானது x இன் மதிப்பு +2 ஆக இருப்பதை நாம் கண்டோம். எனவே, மேற்காணும் நேர்க்கோட்டு அமைப்பை இயற்கணிதச் சமன்பாடாக y = x + 2 எனக் குறிப்பிடலாம். இவ்வாறான சமன்பாடு நேர்க்கோட்டுச் சமன்பாடு (ஒருபடிச்சமன்பாடு) எனப்படும். மேலும், இந்த நேர்க்கோட்டுக்கான வரைபடமானது 'நேர்க்கோட்டு வரைபடம்' எனப்படும். நேர்க்கோட்டுச் சமன்பாடுகளில் ஒன்று அல்லது அதற்கு மேற்பட்ட மாறிகளைப் பயன்படுத்துகிறோம். அவற்றுள் ஒரு மாறியானது மற்றொன்றைச் சார்ந்து உள்ளது.

வாடகை மகிழுந்தில் அதிக தூரம் பயணம் செய்தால், அதிகக் கட்டணத்தை நாம் செலுத்த வேண்டும். இங்கு பயண தூரமானது சாராத மாறிக்கு எடுத்துக்காட்டு ஆகும். வாடகைக் கட்டணம் பயணம் செய்த தூரத்தைச் சார்ந்து இருப்பதால், வாடகைக் கட்டணமானது சார்ந்த மாறி எனப்படும்.

ஒருவர் மின்சாரத்தை எவ்வளவு அதிகம் பயன்படுத்துகிறாரோ, அந்த அளவிற்கு அதிக மின்சாரக் கட்டணத்தைச் செலுத்த வேண்டி வரும். நாம் பயன்படுத்தும் மின்சாரமானது சாராத மாறி ஆகும். ஆகவே, இயல்பாகவே மின்சாரக் கட்டணத் தொகை ஆனது சார்ந்த மாறி ஆகும்.

2. இரண்டு மாறிகளில் அமைந்த நேர்க்கோட்டுச் சார்பு வரைபடம்

வடிவியலில் நாம் இணைகோடுகள், வெட்டும் கோடுகள் போன்றவற்றைப் பற்றி படித்துள்ளோம். ஆனால், உண்மையில் அவை எவ்வளவு தூரத்தில் அமைந்துள்ளன அல்லது எங்கு அமைந்துள்ளன என நாம் பார்த்தது இல்லை. வரைபடத்தாளில் வரைவதால் அவற்றின் இடங்களைக் காண முடிகிறது. ஒரு நேர்க்கோட்டுச் சமன்பாடு இரண்டு மாறிகளில் அமைந்த சமன்பாடு எனில், அந்த வரைபடம் ஒரு நேர்க்கோட்டைக் குறிக்கும். நேர்க்கோட்டுச் சமன்பாட்டை வரைபடத்தில் வரைய குறைந்தபட்சம் இரண்டு புள்ளிகள் நமக்குத் தேவை. ஆனால் இரண்டுக்கும் மேற்பட்ட புள்ளிகளைப் பயன்படுத்தி வரைவது பாதுகாப்பானது (ஏன்?) புள்ளிகளைத் தேர்ந்தெடுக்கும் போது மிகை, குறை மற்றும் பூச்சிய மதிப்புகளைப் (முழுக்கள்) பயன்படுத்துவது நமக்கு நன்மை பயக்கும். ஒரு சோடிப் புள்ளிகளின் வழியாக தனித்துவமான ஒரே ஒரு நேர்க்கோடு மட்டுமே செல்லும்.

எடுத்துக்காட்டு 3.44 

y = 5x என்ற சமன்பாட்டிற்கு வரைபடம் வரைக.

தீர்வு:

கொடுக்கப்பட்ட y = 5x என்ற சமன்பாட்டில் y என்பது x இன் மதிப்பைப் போல் 5 மடங்கு ஆகும்.

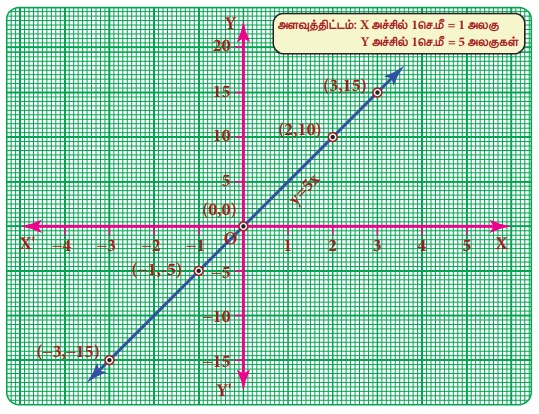
(–3,–15) (–1,–5) (0,0) (2,10) (3,15) ஆகிய புள்ளிகளை வரைபடத்தாளில் குறித்து, அவற்றை இணைக்க, நமக்கு y = 5x என்ற நேர்க்கோடு கிடைக்கிறது.

எடுத்துக்காட்டு 3.45

y = x + 1 என்ற சமன்பாட்டிற்கு வரைபடம் வரைக. 

x மற்றும் y ஆகியவற்றிற்கு இரண்டு மதிப்புகளைத் தேர்ந்தெடுத்து தொடங்குவோம். முதலில் 

(i) x மதிப்பு 0 ஆக இருக்கும்போது y மதிப்பு என்னவாக இருக்கும். மேலும் 

(ii) y மதிப்பு 0 ஆக இருக்கும்போது x மதிப்பு என்னவாக இருக்கும் என அறியலாம். மேலும் ஒன்று அல்லது இரண்டுக்கும் அதிகமான மதிப்புகளைப் பிரதியிட்டுக் காண்போம்.

குறைந்தபட்சம் இன்னும் இரண்டு வரிசைச் சோடிகளையாவது கண்டுபிடிக்க வேண்டும். எளிமையாக வரைய பின்னவடிவ மதிப்புகளைத் தவிர்க்க வேண்டும். சரியான சோடிப் புள்ளிகளை ஊகிக்க வேண்டும்.

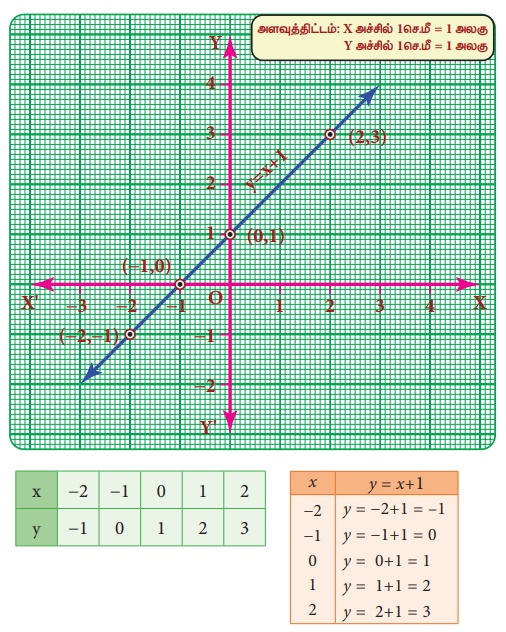
இப்போது நாம் (–2,–1) (–1,0) (0,1) (1,2) (2,3) ஆகிய ஐந்து புள்ளிகளை வரைபடத்தாளில் குறித்து, அவற்றை இணைக்க நமக்கு y =  x + 1 என்ற நேர்க்கோட்டு கிடைக்கிறது.

குறிப்பு

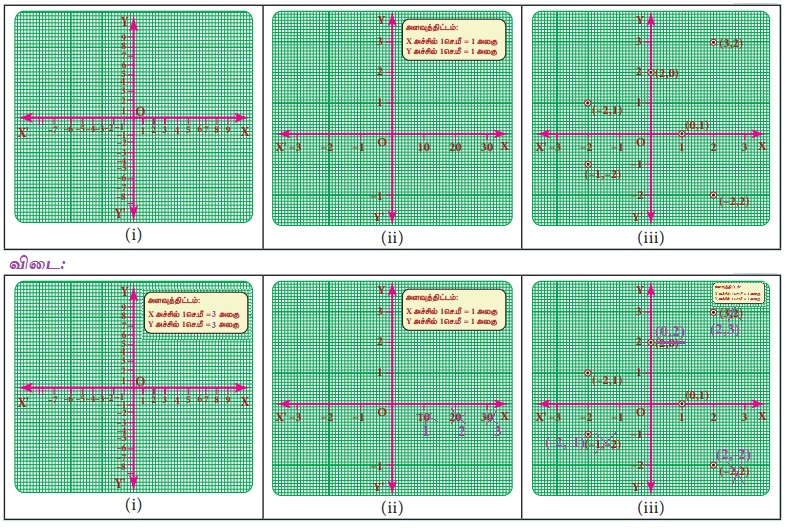
தேர்ந்தெடுக்கும் அளவுத்திட்டத்தைப் பொறுத்து வரைப்படத்தின் நிலை மாறுபடும்

இவற்றை முயல்க

கீழ்க்காணும் வரைபடத்தில் தவறுகளை கண்டறிந்து சரி செய்க.