இரு மாறிகளில் அமைந்த நேரியச் சமன்பாடு (Linear Equation in Two Variables)

இரு மாறிகளில் அமைந்த நேரியச் சமன்பாடு (Linear Equation in Two Variables)

இரு மாறிகளில் அமைந்த ஒரு நேரியச் சமன்பாட்டின் பொது வடிவம் ax + by + c = 0 ஆகும். இதில், a,b,c ஆகியன மெய்யெண்கள், a மற்றும் b ஆகிய இரண்டும் பூச்சியமற்றவை (x, y என்பன இரண்டு மாறிகள், c என்பது மாறிலி).

எடுத்துக்காட்டுகள்

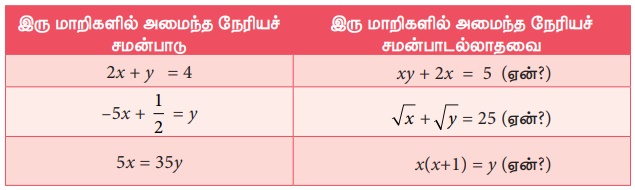
ஒரு படியில் அமைந்த இரண்டு மாறிகளைக் கொண்டதும் அந்த இரண்டு மாறிகளின் பெருக்குதல் இல்லாமலும் அமையும் சமன்பாடானது இரு மாறிகளில் அமைந்த நேரியச் சமன்பாடாகும். (இரு மாறிகளில் அமைந்த ஒரு சமன்பாட்டின் படி 1 எனில் அச்சமன்பாடு இரு மாறியில் அமைந்த நேரியச் சமன்பாடு எனப்படும்).

உதாரணமாக 2x + y = 4 என்பது நேரியச் சமன்பாடாகுமா? நீங்கள் நினைப்பது சரிதான். ஏனென்றால் இச்சமன்பாட்டின் வரைபடம் ஒரு நேர்க்கோடாகும். அதனைச் சரிபார்ப்போமா ?

2x + y = 4 என்ற வரைபடம் வரைய சில புள்ளிகளை எடுத்துக்கொண்டு அவற்றை நாம் இணைக்க வேண்டி இருக்கிறது. (அப்புள்ளிகளே சமன்பாட்டை நிறைவு செய்யும் வரிசைச் சோடிகள் ஆகும்). கொடுக்கப்பட்டுள்ள சோடிப் புள்ளிகளைக் கொண்டு 2x + y = 4 என்ற சமன்பாட்டிற்கு அட்டவணையைத் தயாரிக்க

y = 4 − 2x என்பதாக எடுத்துக்கொள்வோம். (ஏன்? எப்படி?)

 x = −4 எனில், y = 4 − 2(−4) = 4 + 8 = 12 

x = −2 எனில், y = 4 − 2(−2) = 4 + 4 = 8 

x = 0 எனில், y = 4 − 2(0) = 4 + 0 = 4 

x = +1 எனில், y = 4 − 2(+1) = 4 − 2 = 2 

x = +3 எனில், y = 4 − 2(+3) = 4 − 6 = −2 

இந்த மதிப்புகளைக் பின்வருமாறு அட்டவணைப்படுத்தலாம்:

 (ஒரு கோட்டினை அமைக்க, நமக்குப் பல புள்ளிகள் தேவைப்படுகிறதா? ஒரு கோட்டினை அமைக்க இரண்டு புள்ளிகள் போதுமானது. இதைச் சரிபார்ப்பதற்காகக் கூடுதலாக ஒரு புள்ளியினை எடுத்துக்கொள்ளலாம்).

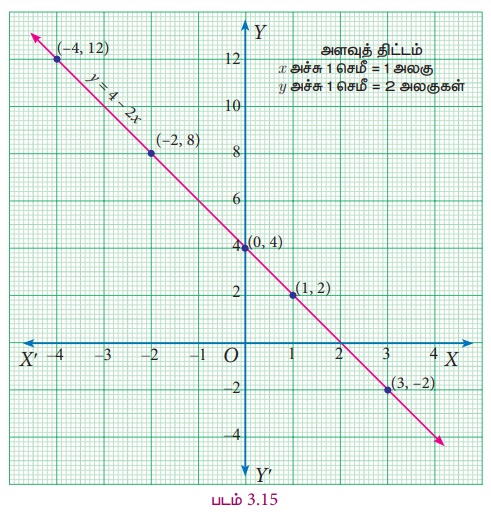
 (−4,12), (−2,8), (0,4), (1,2) மற்றும் (3,−2) ஆகிய புள்ளிகளை வரைபடத்தில் குறிக்கும்பொழுது அவை ஒரே நேர்க்கோட்டில் அமைவதைக் காணலாம். இதிலிருந்து 2x + y = 4 என்ற சமன்பாடு ஒரு நேர்க்கோடாக அமைகிறது என்பது தெளிவாகின்றது. (ஆகவே இது ஒரு நேரிய சமன்பாடு எனப்படுகிறது).

கோட்டின் மீதுள்ள அனைத்துப் புள்ளிகளும் இந்தச் சமன்பாட்டினை நிறைவு செய்வதால் கோட்டின் மீதுள்ள அனைத்துப் புள்ளிகளின் வரிசைச் சோடிகளும் அச்சமன்பாட்டின் தீர்வுகளாகும்.

எடுத்துக்காட்டு 3.42

பின்வருவனவற்றிற்கு வரைபடம் வரைக.

(i) y = 3x−1

(ii) y = (2/3)x+3

தீர்வு

(i) y = 3x − 1 என்ற கோட்டிற்கான புள்ளிகளின் வரிசைச் சோடிகளைக் காண்பதற்கு அட்டவணையைத் தயாரிக்கலாம்.

 x−இன் மதிப்பாக எந்த மதிப்பை வேண்டுமென்றாலும் எடுத்துக்கொள்ளலாம், இங்கு −1, 0 மற்றும் 1 ஐ மட்டுமே எடுத்துக்கொள்வோம்.

x = −1 எனில், y = 3(−1)−1 = −4 

x = 0 எனில், y = 3(0)−1 = −1 

x = 1 எனில், y = 3(1)−1 = 2

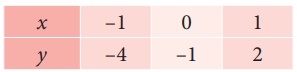
குறிக்க வேண்டிய புள்ளிகள் (x,y) : (−1, −4), (0, −1), (1, 2). 

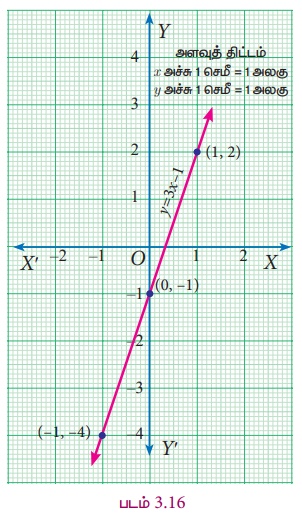
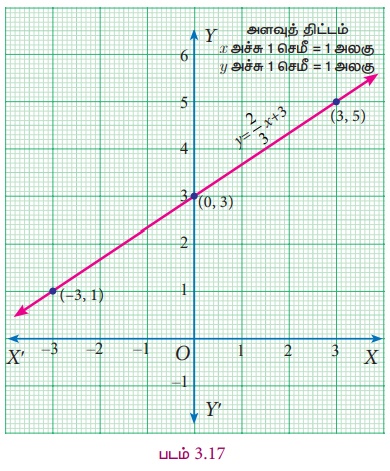
(ii) y = (2/3)x+3 என்ற கோட்டின் புள்ளிகளின் வரிசைச் சோடிகளைக் காண்பதற்கான அட்டவணையைத் தயாரிக்கலாம்.

x இன் மதிப்புகளை −3, 0, 3 என எடுத்துக்கொள்கிறோம். (ஏன்?)

x=−3 எனில், y = 2/3(−3) +3=1 

x=0 எனில், y = 2/3(0)+ 3 = 3 

x=3 எனில், y = 2/3(3) + 3 = 5

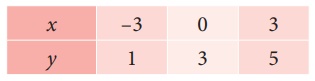
குறிக்க வேண்டிய புள்ளிகள் (x,y) :

(−3,1), (0,3), (3,5).

1. ஒருங்கமைந்த நேரிய சமன்பாடுகள் (Simultaneous Linear Equations)

சமன்பாடுகளை வரைபடத்தில் குறிப்பது பற்றி ஏற்கனவே அறிந்த நாம், தற்போது சமன்பாடுகளின் தொகுப்பு குறித்தும், குறிப்பாக இரண்டு ஒருங்கமைந்த நேரியச் சமன்பாடுகளைப் பற்றி கற்க இருக்கிறோம்.

ஒருங்கமைந்த நேரிய சமன்பாடுகள் என்றால் என்ன? இரண்டு அல்லது அதற்கும் மேற்பட்ட நேரிய சமன்பாடுகள் ஒரே வகையான மாறிகளைக் கொண்டிருந்தால் அவை ஒருங்கமைந்த நேரிய சமன்பாடுகள் ஆகும். 

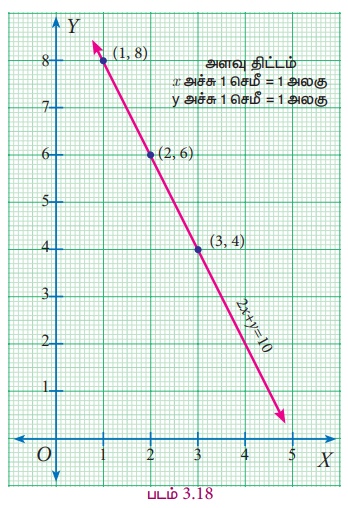
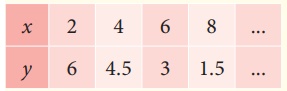
இவை ஏன் நமக்குத் தேவைப்படுகின்றன? 2x + y = 10 ஐப் போன்ற ஒரு சமன்பாட்டிற்கு எண்ணற்ற தீர்வுகள் உண்டு . (1,8), (2,6), (3,4) மற்றும் மேலும் சில புள்ளிகளும் வரைபடத்தில் உள்ள கோட்டின் மீது அமையும் முடிவுறாத தீர்வுகளாகும்.

இது போன்ற ஒரு சமன்பாட்டைத் தீர்ப்பதற்கு, இதனுடன் சேர்த்து மற்றொரு சமன்பாட்டையும் பயன்படுத்தினால் மட்டுமே ஒரே நேரத்தில் இந்த இரண்டு சமன்பாடுகளையும் தீர்க்கும் ஒரு வரிசைச் சோடியைத் தீர்வாகப் பெற முடியும். இதுபோன்று இரண்டு சமன்பாடுகளை ஒருங்கிணைத்துத் தீர்க்கக் கிடைக்கும் அர்த்தமுள்ள சூழ்நிலைகளை ஏற்படுத்தும் சமன்பாடுகளை ஒருங்கமைந்த நேரிய சமன்பாடுகள் என்கிறோம்.

ஒருங்கமைந்த நேரிய சமன்பாடுகளை நடைமுறை வாழ்க்கைச் சூழ்நிலையின் மூலம் புரிந்துகொள்ளுதல்.

அனிதா இரண்டு அழிப்பான்களையும் ஒரு கரி எழுதுகோலையும் ₹10 இக்கு வாங்கினாள் என்று கருதுக. அவற்றின் தனிப்பட்ட விலை பற்றி அனிதாவிற்குத் தெரியவில்லை. ஓர் அழிப்பானின் விலையை x எனவும், ஒரு கரி எழுதுகோலின் விலையை y எனவும் கொண்டு இதற்கு ஒரு சமன்பாட்டினை நாம் அமைப்போம். 

அதாவது, 2x + y = 10         ... (1) 

இப்பொழுது, ஓர் அழிப்பான் மற்றும் ஒரு கரி எழுதுகோலின் விலையைத் தனித்தனியாக அறிந்துகொள்ள அனிதா விரும்புகிறாள்.

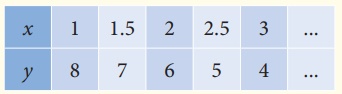
அதற்காக அவள் x மற்றும் y இக்குப் பல மதிப்புகளைப் பயன்படுத்தி சமன்பாடு (1) இக்கு தீர்வு காண முயற்சி செய்கிறாள். 

 2 " ஓர் அழிப்பானின் விலை + ஒரு கரி எழுதுகோலின் விலை = ₹10 

2(1)+8 =10

2(1.5)+7 =10 

2(2)+6 =10 

2(2.5)+5 =10

2(3)+4 =10

குறிக்க வேண்டிய புள்ளிகள் :

அவள் எண்ணற்ற விடைகளைப் பெறுகிறாள். ஆகையால் அவள் இரண்டாவது சமன்பாட்டைக் கொண்டு விலையை அறிய முயற்சிக்கிறாள்.

அனிதாவிற்கு மேலும் சில கரி எழுதுகோல்கள் மற்றும் அழிப்பான்கள் தேவைப்படுகிறது. இப்பொழுது அவர் வாங்கிய 3 அழிப்பான்கள் மற்றும் 4 கரி எழுதுகோல்களுக்காகக் கடைக்காரர் மொத்தத் தொகையாக ₹30 ஐப் பெற்றுக்கொள்கிறார். இதற்கு முன்பு அமைத்ததைப் போலவே நாம் மற்றொரு சமன்பாட்டை அமைக்கலாம்.

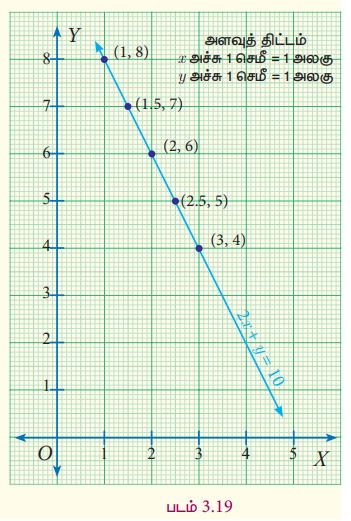
3x + 4y = 30            ... (2) 

இப்பொழுதும் அவள் கீழ்க்கண்டவாறு எண்ணற்ற தீர்வுகளைப் பெறுகிறாள்.

3 “ ஓர் அழிப்பானின் விலை + 4 (ஒரு கரி எழுதுகோலின் விலை) = ₹30

3(2)+4 (6) = 30 

3(4)+4 (4.5) = 30

3(6)+4 (3) = 30 

3(8)+4 (1.5) = 30

         .             .

         .             .

         .             .

குறிக்க வேண்டிய புள்ளிகள் : 

இதனை அவளது ஆசிரியருடன் கலந்துரையாடும்போது அதற்கு அவர் இரண்டு சமன்பாடுகளையும் ஒருங்கே அமைத்துத் தீர்க்கும்போது ஒரே ஒரு தீர்வுதான் கிடைக்கும் என்று கூறினார்.

சமன்பாடு (1) மற்றும் (2) ஐத் தீர்க்க, ஓர் அழிப்பானின் விலை ₹2 என்றும் ஒரு எழுதுகோலின் விலை ₹6 என்றும் பெறுகிறோம். இதனை வரைபடத்தில் (படம் 3.20) காண முடியும்.

இது போன்ற நிகழ்வில் ஓர் அர்த்தமுள்ள சூழ்நிலையை உருவாக்க நம்மால் இணைத்துக் கருதப்படும் சமன்பாடுகளே ஒருங்கமைந்த நேரிய சமன்பாடுகள் எனப்படுகின்றன.

ஆகவே, ஒரே வகையான மாறிகளில் அமைந்த இரண்டு அல்லது அதற்கு மேற்பட்ட நேரிய சமன்பாடுகளை ஒருங்கமைந்த நேரிய சமன்பாடுகள் அல்லது நேரிய சமன்பாடுகளின் தொகுப்பு அல்லது நேரிய சமன்பாடுகளின் சோடி என அழைக்கப்படுகின்றன.

எடுத்துக்காட்டு 3.43

 x − 2y = 7 மற்றும் 2x + 3y = 7 என்ற ஒருங்கமைந்த சமன்பாடுகளுக்கு (5,−1) என்பது தீர்வாகுமா என்பதைச் சரிபார்க்க. 

தீர்வு

கொடுக்கப்பட்டவை 

x − 2y =7             ....(1)

2x + 3y =7             ....(2)

 x = 5, y = −1 எனில், நமக்குக் கிடைப்பது, 

(1) இலிருந்து x − 2y = 5 – 2(−1) = 5 + 2 = 7 (வலது பக்கம்) 

(2) இலிருந்து 2x + 3y = 2(5) + 3(−1) = 10−3 = 7 (வலது பக்கம்)

ஆகவே, x = 5, y = −1 என்ற மதிப்புகளானது சமன்பாடுகள் (1) மற்றும் (2) ஐ ஒரே நேரத்தில் நிறைவு செய்கிறது. ஆகவே, (5,−1) என்பது கொடுக்கப்பட்ட சமன்பாடுகளின் தீர்வாகும்.

முன்னேற்றத்தைச் சோதித்தல்: 2x − 5y − 2 = 0 மற்றும் x + y − 6 = 0 ஆகிய ஒருங்கமைந்த நேரிய சமன்பாடுகளுக்கு (3, 3) என்பது ஒரு தீர்வாகுமா என்பதை வரைபடம் மூலம் சோதித்துப் பார்க்கவும்.

2. ஒருங்கமைந்த நேரிய சமன்பாடுகளைத் தீர்க்கும் முறைகள் (Methods of solving simultaneous linear equations)

ஒருங்கமைந்த நேரிய சமன்பாடுகளைத் தீர்க்கப் பல வழிமுறைகள் உள்ளன. அவற்றைப் பெரும்பாலும் வடிவியல் முறை மற்றும் இயற்கணித முறை என வகைப்படுத்தலாம்.

வடிவியல் முறை 

1. வரைபட முறை 

இயற்கணித முறை 

1. பிரதியிடல் முறை

2. நீக்கல் முறை 

3. குறுக்குப் பெருக்கல் முறை

வரைபட முறையின் மூலம் தீர்வு காணுதல் (Solving by Graphical Method)

இரு மாறிகளில் அமைந்த ஒருபடிச் சமன்பாட்டை எவ்வாறு வரைபடம் வரைந்து விளக்கலாம் என்பதை முன்னரே கண்டுள்ளோம். இங்கு நாம் இரு மாறிகளில் அமைந்த இரு நேரிய சமன்பாடுளின் வரைபடம் வரைந்து அதன் மூலம் ஒருங்கமைந்த நேரிய சமன்பாடுகளுக்கான தீர்வை காண முடியும் என்பதைப் பற்றிக் கற்கப்போகிறோம்.

எடுத்துக்காட்டு 3.44

ஒருங்கமைந்த நேரிய சமன்பாடுகளுக்கு வரைபடம் மூலம் தீர்வு காண்க. x + y = 5; 2x − y = 4. 

தீர்வு

கொடுக்கப்பட்டவை

 x + y = 5          ... (1)

2x − y = 4          ... (2)

 சமன்பாடு (1) இக்கு வரைபடம் வரைதல் எளிது.

முதற்கோட்டின் மீதுள்ள இரண்டு புள்ளிகளின் x மற்றும் y மதிப்புகளை பின்வருமாறு காணலாம்.

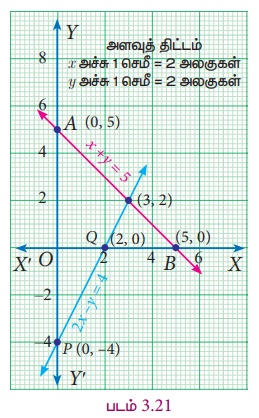
x = 0 எனில், (1) இலிருந்து y = 5 எனக் கிடைக்கும். எனவே, A (0,5) என்பது கோட்டின் மீதுள்ள ஒரு புள்ளியாகும்.

 y = 0 எனில், (1) இலிருந்து x = 5 எனக் கிடைக்கும். எனவே, B(5,0) என்பது கோட்டின் மீதுள்ள மற்றொரு புள்ளியாகும். 

வரைபடத்தில் A மற்றும் B ஆகிய இரண்டு புள்ளிகளைக் குறித்து அவற்றை இணைத்துக் கோடு (1) வரைக.

இதே முறையைப் பயன்படுத்திச் சமன்பாடு (2) இக்கும் வரைபடம் வரையலாம்.

 x = 0 எனில், (2) இலிருந்து y = −4 எனக் கிடைக்கும்.

எனவே (0,−4) என்பது கோட்டின் மீதுள்ள ஒரு புள்ளி. 

y = 0 எனில், (2) இலிருந்து x = 2 எனக் கிடைக்கும். எனவே Q(2,0) என்பது அந்தக் கோட்டின் மீதுள்ள மற்றொரு புள்ளி ஆகும்.

குறிப்பு: கிடைக்கப்பெற்ற தீர்வானது இரண்டு சமன்பாடுகளுக்கும் தீர்வாக அமைகிறதா (நிறைவு செய்கிறதா) என்று சரிபார்த்தல் நலம்.

வரைபடத்தில் P மற்றும் Q ஆகிய புள்ளிகளைக் குறித்து இரண்டு புள்ளிகளையும் இணைத்துக் கோடு (2) வரைக.

இந்த இரு கோடுகளும் ஒன்றையொன்று வெட்டிக்கொள்ளும் புள்ளியான (3,2) என்பது சமன்பாடுகள் (1) மற்றும் (2) இன் தீர்வாகும். இரு கோடுகளுக்கும் ஒரே ஒரு புள்ளி தீர்வாக அமைகிறது. ஆகவே, தீர்வு x = 3, y = 2 ஆகும்.

எடுத்துக்காட்டு 3.45

ஒருங்கமைந்த நேரிய சமன்பாடுகளுக்கு வரைபடம் மூலம் தீர்வு காண்க 3x + 2y = 6; 6x + 4y = 8 

தீர்வு

ஒவ்வொரு கோட்டிற்கும் அட்டவணை தயாரித்து வரிசைச் சோடிப் புள்ளிகளைக் குறிக்கவும்.

3x + 2y = 6 இன் வரைபடம்

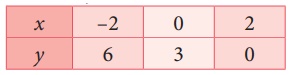
குறிக்கவேண்டிய புள்ளிகள்: (−2,6), (0,3), (2,0)

6x + 4y = 8 இன் வரைபடம்

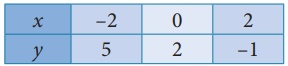
குறிக்கவேண்டிய புள்ளிகள் : (−2,5), (0,2), (2,−1)

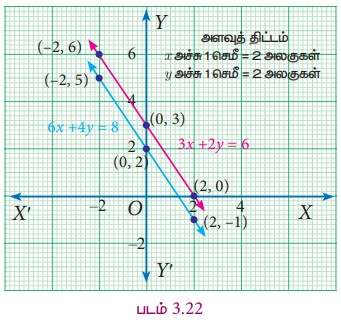
இரண்டு சமன்பாடுகளுக்கும் வரைபடம் வரைந்தால், இரண்டும் ஒன்றுக்கொன்று இணையாக அமைந்து நமக்கு வெட்டும் புள்ளியைக் கொடுக்காததைக் காணலாம். இதன் மூலமாக இரண்டு சமன்பாடுகளுக்கும் பொதுவான வெட்டும்புள்ளி தீர்வாக அமையாததைக் காணலாம். எனவே, இச்சமன்பாடுகளுக்குத் தீர்வு கிடையாது.

எடுத்துக்காட்டு 3.46

ஒருங்கமைந்த நேரிய சமன்பாடுகளுக்கு வரைபடம் மூலம் தீர்வு காண்க  y = 2x + 1; −4x + 2y = 2 

தீர்வு

ஒவ்வொரு கோட்டிற்கும் அட்டவணை தயாரித்து வரிசைச் சோடிப் புள்ளிகளைக் குறிக்கவும்.

 y = 2x + 1 இன் வரைபடம்

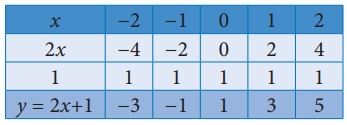
குறிக்கவேண்டிய புள்ளிகள் : (−2, −3), (−1, −1), (0,1), (1,3), (2, 5) 

 − 4x + 2y = 2 இன் வரைபடம்

 2y = 4x + 2

 y = 2x + 1 

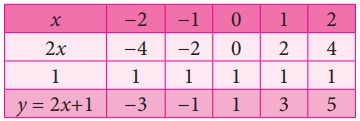
குறிக்கவேண்டிய புள்ளிகள் : (−2, −3), (−1, −1), (0, 1), (1, 3), (2, 5)

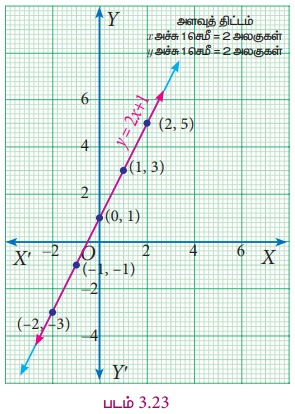
இங்கு, இரு சமன்பாடுகளும் ஒன்றே; ஆனால் இரண்டும் வெவ்வேறு வடிவில் அமைந்துள்ளன. சமன்பாடுகள் இரண்டும் ஒன்றே என்பதால் தீர்வுகளும் ஒரே மாதிரியானவை. இங்கு ஒரு கோட்டின் மீதமைந்த அனைத்துப் புள்ளிகளும் மற்றொரு கோட்டின் மீதே உள்ளன.

எனவே, இங்கு கோட்டின் மீது அமைந்துள்ள அனைத்து வரிசைச் சோடிப் புள்ளிகளும் எண்ணற்ற தீர்வுகளாக அமைகின்றன.

எடுத்துக்காட்டு 3.47

 ஒரு செவ்வகத்தின் சுற்றளவு 36 மீட்டர் மற்றும் நீளமானது அகலத்தின் மூன்று மடங்கை விட 2 மீட்டர் அதிகமெனில், செவ்வகத்தின் பக்க அளவுகளை வரைப்பட முறையைப் பயன்படுத்திக் காண்க. 

தீர்வு

 கொடுக்கப்பட்ட கூற்றுகளுக்கு நாம் சமன்பாடுகளை அமைப்போம்.

 செவ்வகத்தின் நீளம் மற்றும் அகலத்தை முறையே l மற்றும் b என்க.

முதல் கூற்றுக்குச் சமன்பாடு அமைத்தல்

செவ்வகத்தின் சுற்றளவு = 36 மீ

2(l + b) = 36

 l+b= 36/2

 l = 18−b         ……… (1)

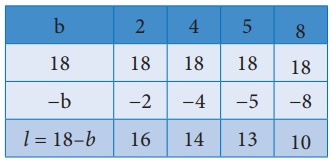
 புள்ளிகள்: (2,16), (4,14), (5,13), (8,10) இரண்டாவது கூற்றுக்குச் சமன்பாடு அமைத்தல் :

இரண்டாவது கூற்றின்படி, நீளமானது அகலத்தின் மூன்று மடங்கை விட 2 மீ அதிகம் எனவே l = 3b+2        .... (2)

சமன்பாடு (2) இக்கு அட்டவணை அமைப்போம்

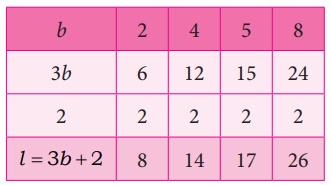
புள்ளிகள் : (2,8), (4,14), (5,17), (8,26)

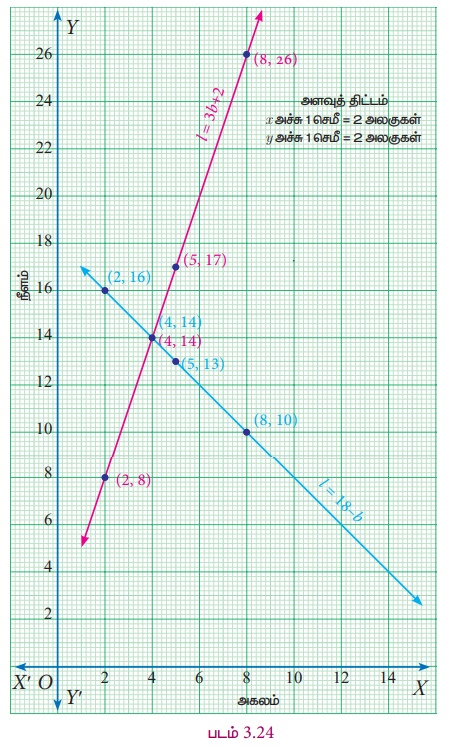
இரண்டு கோடுகளுக்கும் பொதுவான ஒரு புள்ளியே தீர்வாக அமையும். இங்கு (4,14) என்பதே தீர்வாக இருப்பதைக் காணலாம். எனவே தீர்வானது b = 4, l = 14.

சரிபார்த்தல் :

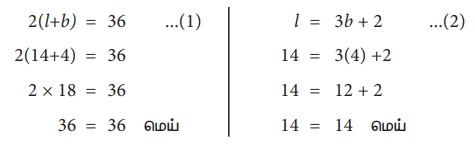
2(l+b) = 36           …………(1)

2(14+4) = 36 

2 × 18 = 36

36 = 36 மெய்

l = 3b + 2            …………(2)

14 = 3(4) +2 

14 = 12 + 2

14 = 14 மெய்