மீதித் தேற்றம் (Remainder Theorem)

மீதித் தேற்றம் (Remainder Theorem)

இப்பகுதியில் மீதியைக் காண எளிய மற்றும் அழகான ஒரு முறையைக் காண்போம்.

ஒரு பல்லுறுப்புக் கோவையை ஒருபடிப் பல்லுறுப்புக் கோவையால் வகுக்க, மீதித் தேற்றம் என அழைக்கப்படும் மிகவும் பிரபலமான இயற்கணிதத் தேற்றத்தைப் பயன்படுத்தலாம்.

 p(x) என்ற பல்லுறுப்புக் கோவையின் படி 1 ஐ விடப் பெரியதாகவோ அல்லது சமமாகவோ இருந்து, அதை (x−a) என்ற நேரியக் கோவையால் வகுக்கக் கிடைக்கும் மீதி p(a) ஆகும். இங்கு a ஒரு மெய்யெண்.

மீதித் தேற்றத்தின் முக்கியத்துவம்: இத்தேற்றத்தின் மூலம் ஒரு பல்லுறுப்புக் கோவையைச் சிக்கலான நீள்வகுத்தல் முறையில் வகுக்காமலேயே அதன் மீதியைக் காண இயலும். 

குறிப்பு:

• p(x) ஐ (x+a) ஆல் வகுக்கக் கிடைக்கும் மீதி p(− a) ஆகும். 

• p(x) ஐ (ax−b) ஆல் வகுக்கக் கிடைக்கும் மீதி p(b/a) ஆகும். 

• p(x) ஐ (ax+b) ஆல் வகுக்கக் கிடைக்கும் மீதி p( − b/a ) ஆகும்.

எடுத்துக்காட்டு 3.11

எடுத்துக்காட்டு 3.12

 f(x) = 2x4 − 6x3 + 3x2 + 3x – 2 என்ற பல்லுறுப்புக் கோவை x2 −3x + 2 என்ற பல்லுறுப்புக் கோவையால் மீதியின்றி வகுபடும் என்று நீள் வகுத்தல் முறையைப் பயன்படுத்தாமல் நிரூபி.

தீர்வு

 f(x) = 2x4 − 6x3 + 3x2 + 3x – 2

 g(x) = x2 – 3x + 2 என்க

= x2 – 2x – x + 2 

= x(x − 2) − 1(x − 2)

= (x − 2)(x − 1) 

மீதித் தேற்றத்தைப் பயன்படுத்தி f(x) என்ற பல்லுறுப்புக் கோவை (x−1), (x−2) என்ற பல்லுறுப்புக் கோவையால் மீதியின்றி வகுபடும் என்று நிரூபிக்க வேண்டும்.

 f(1) = 2(1)4 − 6(1)3 + 3(1)2 + 3(1)− 2

= 2 − 6 + 3 + 3 − 2 = 0

 f(2) = 2(2)4 − 6(2)3 + 3(2)2 + 3(2) − 2

= 32 − 48 + 12 + 6 − 2

= 0

எனவே, f(x) என்ற பல்லுறுப்புக் கோவை (x − 1) (x − 2) ஆல் மீதியின்றி வகுபடும். 

அதாவது, f(x) என்ற பல்லுறுப்புக் கோவை x2 −3x + 2 ஆல் மீதியின்றி வகுபடும்.

 p(x) என்ற பல்லுறுப்புக் கோவையை (x − a) ஆல் வகுக்க மீதி p(a) = 0 எனில், (x − a) என்பது p(x) இன் ஒரு காரணியாகும். மீதித் தேற்றம் காரணித் தேற்றத்திற்கு முன்னெடுத்துச் செல்கிறது. 

1. காரணித் தேற்றம் (Factor Theorem)

 p(x) என்ற பல்லுறுப்புக் கோவையின் படி n ≥ 1 மற்றும் ‘a' என்பது ஒரு மெய்யெண் எனில், 

(i) p(a) = 0 ஆக உள்ளபோது, (x − a) என்பது p(x) இன் ஒரு காரணி ஆகும்.

(ii) (x − a) என்பது p(x) இன் ஒரு காரணி எனில், p(a) = 0 ஆகும்.

நிரூபணம்

 p(x) என்பது வகுபடும் கோவை மற்றும் (x − a) வகுக்கும் கோவை.

பல்லுறுப்புக் கோவைகளின் வகுத்தல் விதியின் படி (division algorithm) p(x) = (x − a) q(x) + p(a) இதில், q(x) என்பது ஈவு மற்றும் மீதி p(a) ஆகும். 

(i) p(a) = 0 எனில், p(x) = (x − a)q(x) ஆகும். மேலும், (x − a) என்பது p(x) இன் ஒரு காரணி.

(ii) (x − a) என்பது p(x) இன் ஒரு காரணியானதால்,

p(x) = (x−a)g(x)

இவ்வாறு,

 p(a) = (a − a)g(a)

= 0 × g(a)

= 0

 (x − a) என்பது p(x) இன் ஒரு காரணி எனில், p(a) = 0 ஆகும்.

சிந்தனைக் களம்

 a(a ≠ 0), b என்பன எவையேனும் இரு முழுக்கள் என்க. a என்பது b இன் வகுத்தி எனில், b = ax இங்கு x என்பது ஒரு முழுக்கள் (Integer) ஆகும்.

குறிப்பு

 • p(a) = 0 எனில், (x − a) என்பது p(x) இன் ஒரு காரணி. (ஏனெனில் x−a = 0, x =a)

 • p(−a) = 0 எனில், (x + a) என்பது p(x) இன் ஒரு காரணி. (ஏனெனில் x+a=0, x = −a)

• p( − b/a ) = 0 எனில், (ax+b) என்பது p(x) இன் ஒரு காரணி.

[ ஏனெனில் ax + b = 0, ax = −b, x = − b/a ]

• p( b/a ) = 0  எனில், (ax−b) என்பது p(x) இன் ஒரு காரணி.

[ ஏனெனில் ax − b = 0, ax = b, x = b/a ] 

• p(a) = 0 மற்றும் p(b) = 0 எனில், (x−a) (x−b) என்பது p(x) இன் ஒரு காரணி.

ஏனெனில்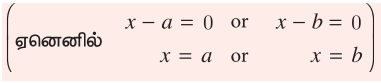

எடுத்துக்காட்டு 3.13

 (x + 2) என்பது x3 – 4x2 − 2x + 20 இன் ஒரு காரணி எனக் காட்டுக.

தீர்வு

p(x) = x3 – 4x2 − 2x + 20 என்க.

காரணித் தேற்றத்தின்படி, (x + 2) என்பது p(x) இன் ஒரு காரணி எனில், மீதி

(x+2) இன் பூச்சியம் காண, 

x + 2 = 0

x = −2

 p(−2) = 0

 p(−2) = (−2)3 − 4(−2)2 − 2(−2) + 20

= −8 – 4(4) + 4 + 20

 p(−2) = 0

எனவே, (x + 2) என்பது .x3 – 4x2 – 2x + 20 இன் ஒரு காரணியாகும்.

எடுத்துக்காட்டு 3.14

 (3x – 2) என்பது 3x3 + x2 − 20x + 12 இன் ஒரு காரணியா? 

தீர்வு

 p(x) = 3x3 + x2 − 20x + 12 என்க.

3x−2 இன் பூச்சியம் காண, 

3x − 2 = 0

3x = 2

x = 2/3

காரணித் தேற்றத்தின்படி, (3x – 2) என்பது p(x) இன் ஒரு காரணி எனில், மீதி p(2/3) = 0 ஆகும்.

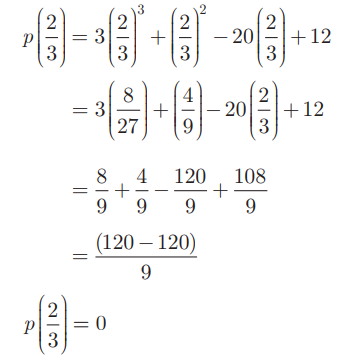
ஆகவே, (3x – 2) என்பது 3x3 + x2 – 20x + 12 இன் ஒரு காரணியாகும்.

முன்னேற்றத்தைச் சோதித்தல்

• p(___) = 0 எனில், (x+3) என்பது p(x) இன் ஒரு காரணி. 

• p(___) = 0 எனில், (3−x) என்பது p(x) இன் ஒரு காரணி. 

• p(____) = 0 எனில், (y−3) என்பது p(y) இன் ஒரு காரணி. 

• p(___) = 0 எனில், (−x−b) என்பது p(x) இன் ஒரு காரணி. 

• p(____) = 0 எனில், (−x+b) என்பது p(x) இன் ஒரு காரணி.

எடுத்துக்காட்டு 3.15

 2x3 – 6x2 + mx + 4 இன் ஒரு காரணி (x − 2) எனில், m இன் மதிப்பு காண்க. 

தீர்வு

p(x) = 2x3 – 6x2 + mx + 4 என்க. 

x−2 இன் பூச்சியம் காண, 

x − 2 = 0

x = 2

காரணித் தேற்றத்தின் படி, மீதி p(2) = 0 எனில், (x − 2) ஒரு காரணியாகும்.

 p(2) =0

2(2)3 − 6(2)2 + m(2) + 4 = 0

2(8) − 6(4) + 2m + 4 = 0

−4+2m = 0

 m = 2