Я«ЄЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«еЯ»ЄЯ«░Я«┐Я«»Я«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (Linear Equation in Two Variables), Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ | Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї | Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї (Solving by Cross Multiplication Method) | 9th Maths : UNIT 3 : Algebra
9 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 3 : Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї
Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї (Solving by Cross Multiplication Method)
Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї (Solving by Cross Multiplication Method)
Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«ЪЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«ЙЯ«ЕЯ«цЯ»Ђ Я«фЯ«▓Я»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«ЋЯ«БЯ«┐Я«цЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»Ђ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ»ђЯ«░Я«┐Я«» Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒ Я«хЯ«┤Я«┐ Я«џЯ»єЯ«»Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ««Я»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«цЯ«ЙЯ«▓Я»Ї Я«ЄЯ«цЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ«┐Я«хЯ«ЙЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ 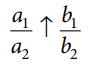 Я«јЯ«ЕЯ»ЇЯ«▒Я«хЯ«ЙЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«џЯ»ІЯ«ЪЯ«┐ Я«еЯ»ЄЯ«░Я«┐Я«» Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ««Я»ѕЯ«хЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е.
Я«јЯ«ЕЯ»ЇЯ«▒Я«хЯ«ЙЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«џЯ»ІЯ«ЪЯ«┐ Я«еЯ»ЄЯ«░Я«┐Я«» Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ««Я»ѕЯ«хЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е.
a1x + b1y + c1 = 0 ....(1)
a2x + b2y + c2 = 0 ....(2)
Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї :
(1) ├Ќ b2 Рѕњ (2) ├Ќ b1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ b2(a1x+b1y+c1) Рѕњ b1(a2x+b2y+c2) = 0
РЄњ x(a1b2 Рѕњ a2b1) = (b1c2 Рѕњ b2c1)
РЄњ x = (b1c2 Рѕњ b2c1) / (a1b2 Рѕњ a2b1)
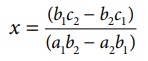
(1) ├Ќ a2 Рѕњ (2) ├Ќ a1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ
y = (c1a2 Рѕњ c2a1) / (a1b2 Рѕњ a2b1)
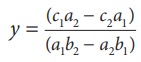
Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«єЯ«ЋЯ«хЯ»Є Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ«ЙЯ«ЕЯ«цЯ»Ђ
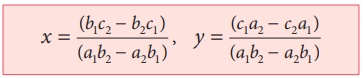
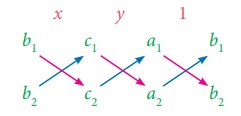
Я«ЄЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї
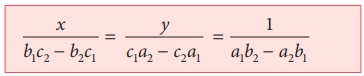
Я«ЄЯ«цЯ«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«▓Я«ЙЯ««Я»Ї
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 3.52
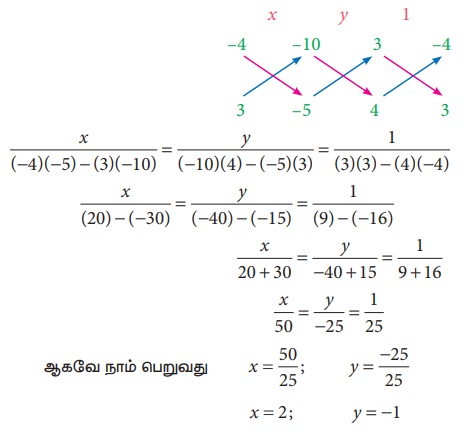
Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ: 3xРѕњ4y=10 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 4x +3y =5
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ
3x Рѕњ 4y = 10 РЄњ 3x Рѕњ 4yРѕњ10 = 0 ...... (1)
4x + 3y = 5 РЄњ 4x +3y Рѕњ5= 0 ......(2)
Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«▓Я»Ї :
3xРѕњ4y = 10 ...(1)
3(2)Рѕњ4(Рѕњ1) = 10
6 + 4 = 10
10 = 10 Я««Я»єЯ«»Я»Ї
4x + 3y = 5 ...(2)
4(2) + 3(Рѕњ1) = 5
8Рѕњ3 = 5
5 = 5 Я««Я»єЯ«»Я»Ї

Я«јЯ«ЕЯ«хЯ»Є Я«цЯ»ђЯ«░Я»ЇЯ«хЯ«ЙЯ«ЕЯ«цЯ»Ђ x = 2, y = Рѕњ1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 3.53
Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ :
3x+5y = 21 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рѕњ7x Рѕњ6y = Рѕњ49
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 3x+5yРѕњ21= 0; Рѕњ7x Рѕњ6y + 49 = 0 Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«ц Я«еЯ«ЙЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ,

Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«▓Я»Ї:
3x+5y = 21 ...(1)
3(7)+5(0) = 21
21 + 0 = 21
21 = 21 Я««Я»єЯ«»Я»Ї
Рѕњ7x Рѕњ 6y = Рѕњ49 ...(2)
Рѕњ7(7) Рѕњ 6(0) = Рѕњ49
Рѕњ49 + 0 = Рѕњ49
Рѕњ49 = Рѕњ49 Я««Я»єЯ«»Я»Ї

Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є y/0 = 1/17 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ y = 0/17 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЋЯ«хЯ»Є Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ y/0 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»Є Я«ЁЯ«ЕЯ»ЇЯ«▒Я«┐, Я«ЁЯ«цЯ«ЕЯ»ѕ 0 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«│Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«ЙЯ«цЯ»Ђ. Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ»ѕ Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»Ђ Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї Я««Я»єЯ«»Я»ЇЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.