இரு மாறிகளில் அமைந்த நேரியச் சமன்பாடு (Linear Equation in Two Variables), எடுத்துக்காட்டு, தீர்வு | இயற்கணிதம் | கணக்கு - பிரதியிடல் முறையில் தீர்வு காணுதல் (Solving by Substitution Method) | 9th Maths : UNIT 3 : Algebra
9 ஆம் வகுப்பு கணக்கு : அலகு 3 : இயற்கணிதம்
பிரதியிடல் முறையில் தீர்வு காணுதல் (Solving by Substitution Method)
பிரதியிடல் முறையில் தீர்வு காணுதல் (Solving by Substitution Method)
இந்த முறையில், ஒரு மாறியின் மதிப்பை மற்றொரு மாறியில் பிரதியிட்டு, இரு மாறிகள் கொண்ட சமன்பாட்டை ஒரு மாறி கொண்ட சமன்பாடாக மாற்றித் தீர்வு (ஒரு சோடி நேரிய சமன்பாடுகளைத் தீர்ப்பதற்குப் பதிலாக) காண்கிறோம். ஒரு மாறியின் மதிப்பை மற்றொரு மாறியில் பிரதியிடுவதால் இதை நாம் பிரதியிடல் முறை என்று அழைக்கிறோம்.
இதற்கான வழிமுறைகள் பின்வருமாறு:
படி 1: கொடுக்கப்பட்ட இரண்டு சமன்பாடுகளில் ஏதேனும் ஒன்றிலிருந்து, ஒரு மாறியின் மதிப்பை மற்றொரு மாறியின் மதிப்பைக் கொண்டு காணவும்.
படி 2: படி 1 இல் பெறப்பட்ட மாறியின் மதிப்பை மற்றொரு சமன்பாட்டில் பிரதியிட்டுத் தீர்க்க ஒரு மாறியின் மதிப்பைப் பெறலாம்.
படி 3: படி 2 இல் பெறப்பட்ட மாறியின் மதிப்பைப் படி 1 இல் பிரதியிட மற்றொரு மாறியின் மதிப்பைப் பெறலாம்..
எடுத்துக்காட்டு 3.48
ஒருங்கமைந்த நேரிய சமன்பாடுகளைப் பிரதியிடல் முறையில் தீர்க்க: x+3y =16 மற்றும் 2x − y = 4
தீர்வு
கொடுக்கப்பட்டவை
x+3y =16 ... (1)
2x − y = 4 ... (2)
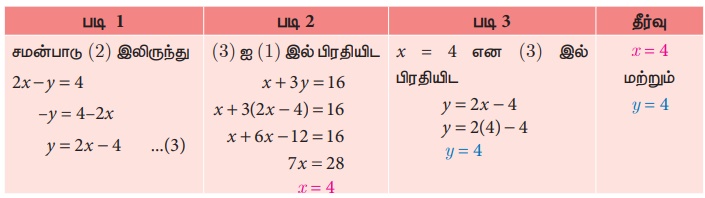
எடுத்துக்காட்டு 3.49
ஓர் ஈரிலக்க எண்ணின் இலக்கங்களின் கூடுதல் 5. அதன் இலக்கங்கள் இடமாற்றப்பட்டால் கிடைக்கும் புதிய எண்ணானது கொடுக்கப்பட்ட எண்ணை விட 27 குறைவு எனில் அந்த எண்ணைக் காண்க.
தீர்வு
x என்பது பத்தாம் இலக்க எண் என்றும் y என்பது ஒன்றாம் இலக்க எண் என்றும் கொள்க.
கொடுக்கப்பட்டவை x + y=5 ... (1)

கொடுக்கப்பட்ட எண் − இடமாற்றபட்ட எண் = 27
(10x+y) − (10y +x) = 27
10x − x+y−10y = 27
9x−9y = 27
x − y =3 .... (2)
x+y = 5 .... (1)
இலிருந்து, y = 5 – x ……..(3)
(3) ஐ (2) இல் பிரதியிட x − (5−x) = 3
x − 5+ x = 3
2x = 8
x = 4
x = 4 என (3) இல் பிரதியிட y = 5−x = 5−4
y = 1
ஆகவே, 10x + y = 10 × 4+1 = 40+1 = 41.
ஆகையால் கொடுக்கப்பட்ட ஈரிலக்க எண் = 41 ஆகும்.
சரிபார்த்தல்:
இலக்கங்களின் கூடுதல் = 5
x + y = 5
4 + 1 = 5
5 = 5 மெய்
கொடுக்கப்பட்ட எண் −
இடமாற்றப்பட்ட எண் = 27
41 − 14 = 27
27 = 27 மெய்