எண்கள் | அலகு 1 | 8 ஆம் வகுப்பு கணக்கு - விகிதமுறு எண்களை ஒப்பிடுதல் | 8th Maths : Chapter 1 : Numbers
8 ஆம் வகுப்பு கணக்கு : அலகு 1 : எண்கள்
விகிதமுறு எண்களை ஒப்பிடுதல்
6. விகிதமுறு எண்களை ஒப்பிடுதல்
பின்வரும் குறிப்புகளை நினைவில் கொள்வது உதவியாக அமையும்:
* ஒவ்வொரு மிகை எண்ணும் பூச்சியத்தை விடப் பெரியதாகும்.
* ஒவ்வொரு குறை எண்ணும் பூச்சியத்தை விடச் சிறியதாகும்.
* ஒவ்வொரு மிகை எண்ணும் ஒவ்வொரு குறை எண்ணை விடப் பெரியதாகும்.
* ஓர் எண்கோட்டின் மீதுள்ள ஓர் எண்ணின் வலதுபுறமாக அமையும் ஒவ்வோர் எண்ணும் அந்த எண்ணைவிடப் பெரியதாகும்.
இரு முழுக்களோ அல்லது பின்னங்களோ கொடுக்கப்பட்டால், நமக்கு அவற்றை எவ்வாறு ஒப்பீடு செய்து அவற்றுள் எது பெரியது அல்லது சிறியது எனக் கூற இயலும். இப்போது, அவ்வாறே நாம் ஒரு சோடி விகிதமுறு எண்களை ஒப்பிடுவோம்.
வகை 1: எதிரெதிர் குறிகளைக் கொண்ட இரு விகிதமுறு எண்களை ஒப்பிடுதல்
எடுத்துக்காட்டு 1.3
![]() மற்றும்
மற்றும் ![]() ஆகியவற்றை ஒப்பிடுக.
ஆகியவற்றை ஒப்பிடுக.
தீர்வு:
ஒவ்வொரு மிகை எண்ணும் குறை எண்ணை விட பெரியது என்பதால், நாம் ![]() >
> ![]() என நாம் முடிவு செய்கிறோம்.
என நாம் முடிவு செய்கிறோம்.
வகை 2: ஒரே பகுதிகளைக் கொண்ட இரு விகிதமுறு எண்களை ஒப்பிடுதல்
எடுத்துக்காட்டு 1.4
![]() மற்றும்
மற்றும் ![]() ஆகியவற்றை ஒப்பிடுக.
ஆகியவற்றை ஒப்பிடுக.
தீர்வு:
பகுதி எண்கள் சமமாக இருப்பதால், தொகுதிகளை மட்டும் ஒப்பீடு செய்தல் போதுமானதாகும்.
1 < 4 என்பதால், ![]() <
< ![]() என நாம் முடிவு செய்கிறோம்.
என நாம் முடிவு செய்கிறோம்.
வகை 3: வெவ்வேறு பகுதிகளைக் கொண்ட இரு விகிதமுறு எண்களை ஒப்பிடுதல்
எடுத்துக்காட்டு 1.5
![]() மற்றும்
மற்றும் ![]() ஆகியவற்றை ஒப்பிடுக.
ஆகியவற்றை ஒப்பிடுக.
தீர்வு:
பகுதிகளின் மீ.சி.ம 12 ஆகும். (கண்டுபிடிக்கவும்!) ஒவ்வொரு விகிதமுறு எண்ணிற்கும் 12 ஐ பகுதியாகக் கொண்ட ஒரு சமான விகிதமுறு எண்ணைக் கண்டறிக. நாம் பெறுவது ![]() =
= ![]() மற்றும்
மற்றும் ![]() =
= ![]() ஆகும். இப்போது, இவை ஓரின பின்னங்கள் ஆகும்.
ஆகும். இப்போது, இவை ஓரின பின்னங்கள் ஆகும்.
இங்கு, ![]() <
< ![]() ஆகவே, நாம்
ஆகவே, நாம் ![]() <
< ![]() என முடிவு செய்கிறோம்.
என முடிவு செய்கிறோம்.
வகை 4: திட்ட வடிவில் இல்லாத இரு விகிதமுறு எண்களை ஒப்பிடுதல்
எடுத்துக்காட்டு 1.6
![]() மற்றும்
மற்றும் ![]() ஆகியவற்றை ஒப்பிடுக.
ஆகியவற்றை ஒப்பிடுக.
தீர்வு:
![]() என்ற எண்ணானது திட்ட வடிவில் இல்லை. முதலில் அதை திட்ட வடிவில் எழுத வேண்டும்.
என்ற எண்ணானது திட்ட வடிவில் இல்லை. முதலில் அதை திட்ட வடிவில் எழுத வேண்டும்.
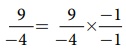 (மிகை பகுதியைப் பெற) =
(மிகை பகுதியைப் பெற) = ![]()
இப்போது நாம் ![]() மற்றும்
மற்றும் ![]() ஐ ஒப்பிடலாம். இவை இரண்டும் வேற்றின பின்னங்கள் என நாம் காண்கிறோம். அவற்றை ஓரின பின்னங்களாக மாற்ற நாம் அவற்றின் மீ.சி.ம ஆன 12 ஐ பயன்படுத்தலாம்.
ஐ ஒப்பிடலாம். இவை இரண்டும் வேற்றின பின்னங்கள் என நாம் காண்கிறோம். அவற்றை ஓரின பின்னங்களாக மாற்ற நாம் அவற்றின் மீ.சி.ம ஆன 12 ஐ பயன்படுத்தலாம்.
இப்போது நாம் அவற்றின் சமான பின்னங்கள் 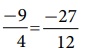 மற்றும்
மற்றும் 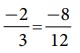 ஆகியவற்றை ஒப்பிடலாம் (எவ்வாறு?)
ஆகியவற்றை ஒப்பிடலாம் (எவ்வாறு?)
நாம் பகுதிகள் சமமாக உள்ளதை பார்க்கிறோம். ஆகவே, தொகுதிகளான −27 மற்றும் −8 ஐ மட்டும் ஒப்பிடுவது போதுமானதாகும்.
எண்கோட்டின் மீது அந்த எண்களைக் குறித்துப் பார்த்தால், நாம் பார்ப்பது

−8 ஆனது −27 இன் வலதுபுறமாக உள்ளது. ஆகவே, (−8) > (−27) ஆகும். இதனால் கிடைக்கும் முடிவானது 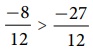 ஆகும். ஆகவே,
ஆகும். ஆகவே, 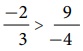 என நாம் முடிவு செய்கிறோம்.
என நாம் முடிவு செய்கிறோம்.
எடுத்துக்காட்டு 1.7
பின்வரும் விகிதமுறு எண்களை ஏறு வரிசை மற்றும் இறங்கு வரிசையில் எழுதுக.
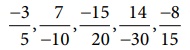
தீர்வு :
முதலில் பகுதிகளை மிகை எண்களாக மாற்றி 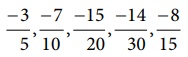 என திட்ட வடிவில் எழுதவும். இங்கு, 5, 10, 15, 20 மற்றும் 30 ஆகியவற்றின் மீ.சி.ம 60 ஆகும் (கண்டுபிடிக்கவும்!). கொடுக்கப்பட்ட விகிதமுறு எண்களை 60 ஐப் பகுதியாகக் கொண்ட சமான பின்னங்களாக மாற்றவும்.
என திட்ட வடிவில் எழுதவும். இங்கு, 5, 10, 15, 20 மற்றும் 30 ஆகியவற்றின் மீ.சி.ம 60 ஆகும் (கண்டுபிடிக்கவும்!). கொடுக்கப்பட்ட விகிதமுறு எண்களை 60 ஐப் பகுதியாகக் கொண்ட சமான பின்னங்களாக மாற்றவும்.
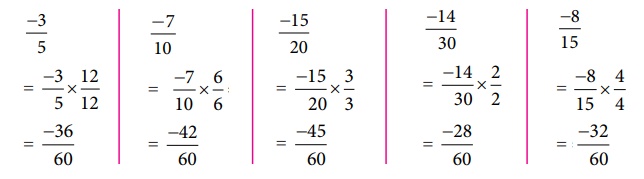
இப்போது −36, −42, −45, −28 மற்றும் −32 ஆகிய தொகுதி எண்களை மட்டும் ஒப்பிட,
−45 < −42 < −36 < −32 < −28 என நாம் காண்கிறோம்.
ஆகவே, 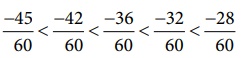 அதாவது,
அதாவது, 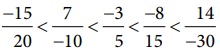 எனவே, ஏறுவரிசையானது
எனவே, ஏறுவரிசையானது 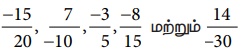 ஆகும். மேலும், அதன் பின்னோக்கு வரிசையான இறங்கு வரிசையானது
ஆகும். மேலும், அதன் பின்னோக்கு வரிசையான இறங்கு வரிசையானது 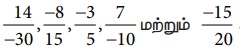 ஆகும்.
ஆகும்.