எண்கள் | அலகு 1 | 8 ஆம் வகுப்பு கணக்கு - கொடுக்கப்பட்ட இரு எண்களுக்கிடையே விகிதமுறு எண்களைக் காணுதல் | 8th Maths : Chapter 1 : Numbers
8 ஆம் வகுப்பு கணக்கு : அலகு 1 : எண்கள்
கொடுக்கப்பட்ட இரு எண்களுக்கிடையே விகிதமுறு எண்களைக் காணுதல்
7. கொடுக்கப்பட்ட இரு எண்களுக்கிடையே விகிதமுறு எண்களைக் காணுதல்
4 மற்றும் 10 ஆகிய முழுக்களை எடுத்துக் கொள்வோம். அவற்றிற்கிடையே நாம் 5, 6, 7, 8 மற்றும் 9 என ஐந்து முழுக்களை இடம் குறிக்கலாம் அல்லவா?

3 இக்கும் −2 இக்கும் இடையே எத்தனை முழுக்களை உங்களால் காண முடியும்? அவற்றைப் பட்டியலிடவும்.
−5 மற்றும் −4 இக்கு இடையே முழுக்கள் ஏதேனும் உள்ளனவா? இல்லை என்பதே பதிலாகும்.

இதன் மூலம் கொடுக்கப்பட்ட இரு முழுக்கள் இடையே முழுக்களின் தேர்வானது வரையறுக்கப்பட்டதாகும் என்பது தெளிவாகிறது. அவை முடிவுடைய எண்ணிக்கையிலோ அல்லது அவற்றிற்கிடையே ஏதும் இல்லாமலோ இருக்கலாம். முழுக்களுக்குப் பதிலாக நாம் விகிதமுறு எண்களை எடுத்துக் கொண்டால் என்ன ஆகும்? என்பதைப் பற்றி நாம் சிந்திக்கலாம். இரு விகிதமுறு எண்களுக்கிடையே பல விகிதுமுறு எண்கள் உள்ளன என்பதனை நாம் காண இருக்கிறோம். இரு விகிதமுறு எண்களுக்கிடையே பல விகிதுமுறு எண்களைக் காண குறைந்தது இரு வழிமுறைகள் உள்ளன.
சராசரிகள் முறை:
இரு எண்களின் சராசரியானது எப்போதும் அந்த இரு எண்களின் நடுவில் அமையும் என்பது நமக்குத் தெரியும். எடுத்துக்காட்டாக, 2 மற்றும் 8 இன் சராசரியானது 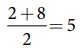 ஆகும். பின்வரும் எண்கோட்டில் காட்டியுள்ளவாறு இந்த 5 ஆனது 2 மற்றும் 8 இன் நடுவில் உள்ளது.
ஆகும். பின்வரும் எண்கோட்டில் காட்டியுள்ளவாறு இந்த 5 ஆனது 2 மற்றும் 8 இன் நடுவில் உள்ளது.
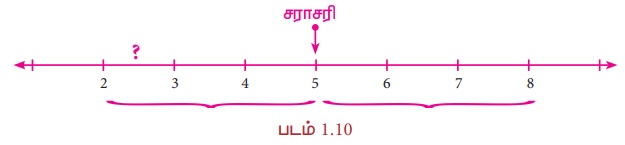
இந்த கருத்தை, இரு விகிதமுறு எண்களுக்கிடையே கூடுதலான விகிதமுறு எண்களைக் காண நாம் பயன்படுத்தலாம்.
எடுத்துக்காட்டு 1.8
![]() மற்றும்
மற்றும் ![]() ஆகியவற்றிற்கு இடையே ஒரு விகிதமுறு எண்ணைக் காண்க.
ஆகியவற்றிற்கு இடையே ஒரு விகிதமுறு எண்ணைக் காண்க.
தீர்வு:
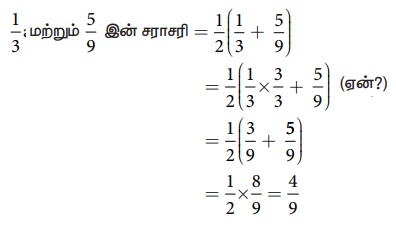
![]() மற்றும்
மற்றும் ![]() இக்கு இடையே நாம் கண்ட ஒரு விகிதமுறு எண்ணானது
இக்கு இடையே நாம் கண்ட ஒரு விகிதமுறு எண்ணானது ![]() ஆகும். இதுபோன்று மேலும் பல எண்களை
ஆகும். இதுபோன்று மேலும் பல எண்களை ![]() மற்றும்
மற்றும் ![]() இக்கு இடையே நம்மால் காண இயலும். இரு விகிதமுறு எண்களுக்கிடையே எண்ணிலடங்கா விகிதமுறு எண்கள் உள்ளன என்பது இதன் மூலம் தெளிவாகிறது. கணிதரீதியாக, கொடுக்கப்பட்ட இரு விகிதமுறு எண்களுக்கிடையே, முடிவில்லாத எண்ணிக்கையிலான விகிதமுறு எண்கள் உள்ளன என நாம் கூறுகிறோம்.
இக்கு இடையே நம்மால் காண இயலும். இரு விகிதமுறு எண்களுக்கிடையே எண்ணிலடங்கா விகிதமுறு எண்கள் உள்ளன என்பது இதன் மூலம் தெளிவாகிறது. கணிதரீதியாக, கொடுக்கப்பட்ட இரு விகிதமுறு எண்களுக்கிடையே, முடிவில்லாத எண்ணிக்கையிலான விகிதமுறு எண்கள் உள்ளன என நாம் கூறுகிறோம்.
சிந்திக்க
![]() இக்கும்
இக்கும் ![]() இக்கும் இடையே ஏதேனும் விகிதமுறு எண்கள் உள்ளனவா?
இக்கும் இடையே ஏதேனும் விகிதமுறு எண்கள் உள்ளனவா?
சமான விகிதமுறு எண்கள் முறை:
கொடுக்கப்பட்ட இரு விகிதமுறு எண்களுக்கிடையே கூடுதலான விகிதமுறு எண்களைப் பெற நாம் சமான பின்னங்களின் கருத்தைப் பயன்படுத்தலாம். இது பின்வரும் விளக்கத்தில் தெளிவாக விவரிக்கப்பட்டுள்ளது.
விளக்கம்:
இப்போது நாம் ![]() மற்றும்
மற்றும் ![]() இக்கு இடையில் கூடுதலான விகிதமுறு எண்களைப் பின்வரும் பட விளக்கத்தின் மூலம் காண முயற்சிக்கலாம். நாம் சமான விகிதமுறு எண்களின் பகுதியின் மடங்குகளைப் பெற்றால் (10 ஆல் பெருக்குவது என்பது எளிதான ஒன்றாகும்) நம்மால் தேவையான அளவிற்கு பல விகிதமுறு எண்களைச் செருக இயலும்.
இக்கு இடையில் கூடுதலான விகிதமுறு எண்களைப் பின்வரும் பட விளக்கத்தின் மூலம் காண முயற்சிக்கலாம். நாம் சமான விகிதமுறு எண்களின் பகுதியின் மடங்குகளைப் பெற்றால் (10 ஆல் பெருக்குவது என்பது எளிதான ஒன்றாகும்) நம்மால் தேவையான அளவிற்கு பல விகிதமுறு எண்களைச் செருக இயலும்.
இங்கு நாம் ![]() ஐ
ஐ ![]() எனவும்
எனவும் ![]() ஐ
ஐ ![]() எனவும் எழுதலாம். இங்கு
எனவும் எழுதலாம். இங்கு ![]() மற்றும்
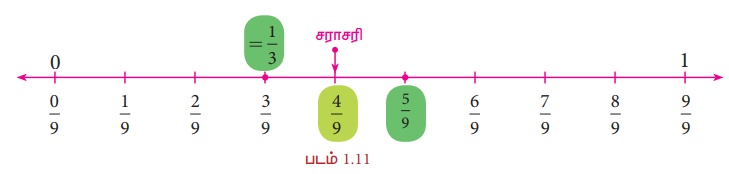
மற்றும் ![]() இக்கு இடையில் 9 விகிதமுறு எண்கள் இருப்பதைப் பின்வரும் எண்கோட்டில் காண்கிறோம்.
இக்கு இடையில் 9 விகிதமுறு எண்கள் இருப்பதைப் பின்வரும் எண்கோட்டில் காண்கிறோம்.

மேலும், நமக்கு ![]() மற்றும்
மற்றும் ![]() இக்கு இடையில் பல விகிதமுறு எண்களை காண வேண்டும் எனில்,
இக்கு இடையில் பல விகிதமுறு எண்களை காண வேண்டும் எனில், ![]() ஐ
ஐ ![]() எனவும்
எனவும் ![]() ஐ
ஐ ![]() எனவும் எழுதினால், அப்போதும் அவற்றிற்கிடையில்
எனவும் எழுதினால், அப்போதும் அவற்றிற்கிடையில் 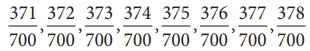 மற்றும்
மற்றும் ![]() என 9 விகிதமுறு எண்களை நாம் பெறலாம்.
என 9 விகிதமுறு எண்களை நாம் பெறலாம்.
பின்வரும் படமானது, ஒரு உருப்பெருக்கி கண்ணாடியின் மூலம், 0 மற்றும் 1 இக்கு இடையிலுள்ள பின்னப்பகுதிகளைப் பெரிதாக்கிப் பார்த்து, அவற்றிற்கு இடையில் பல விகிதமுறு எண்களைக் காண முடியும் என்பதைத் தெளிவாகப் புரிந்து கொள்ள உதவுகிறது.
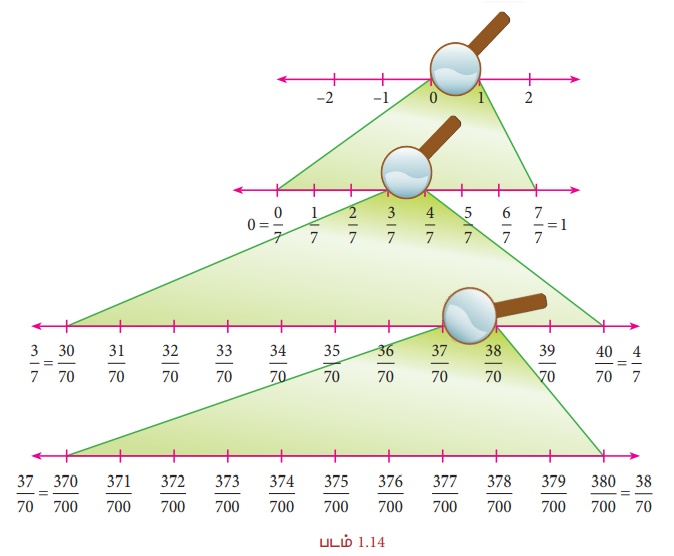
ஆகவே, இரு விகிதமுறு எண்களுக்கிடையே எண்ணிலடங்கா விகிதமுறு எண்கள் உள்ளன என்பது இதன் மூலம் தெளிவாகிறது.
எடுத்துக்காட்டு 1.9
![]() மற்றும்
மற்றும் ![]() ஆகியவற்றுக்கு இடையே குறைந்தது இரண்டு விகிதமுறு எண்களைக் காண்க.
ஆகியவற்றுக்கு இடையே குறைந்தது இரண்டு விகிதமுறு எண்களைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட விகிதமுறு எண்களின் பகுதிகள் வெவ்வேறானவை. 4 மற்றும் 5 இன் மீ.சி.ம 20 ஆகும். இவற்றை 20 ஐ பகுதியாக கொண்ட விகிதமுறு எண்களாக மாற்றவும். இங்கு,
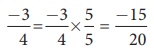 மற்றும்
மற்றும் 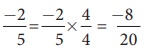 ஆகும்.
ஆகும்.
இப்போது, ![]() மற்றும்
மற்றும் ![]() ஆகியவற்றுக்கு இடையே விகிதமுறு எண்களைக் கண்டு செருகுவது என்பது கீழே காட்டியுள்ளவாறு எளிதாகும்.
ஆகியவற்றுக்கு இடையே விகிதமுறு எண்களைக் கண்டு செருகுவது என்பது கீழே காட்டியுள்ளவாறு எளிதாகும்.
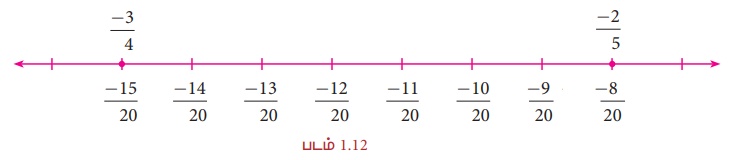
நம்மால் ![]() மற்றும்
மற்றும் ![]() ஆகியவற்றுக்கு இடையே
ஆகியவற்றுக்கு இடையே 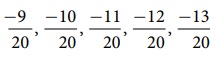 மற்றும்
மற்றும் ![]() என ஒரு சில விகிதமுறு எண்களை பட்டியலிட முடியும்.
என ஒரு சில விகிதமுறு எண்களை பட்டியலிட முடியும்.
![]() மற்றும்
மற்றும் ![]() ஆகியவற்றுக்கு இடையே இந்த விகிதமுறு எண்கள் மட்டுமே உள்ளனவா? சிந்திக்கவும்! முடிந்தால் அவற்றிற்கிடையே மேலும் 10 விகிதமுறு எண்களைக் காண முயற்சிக்கவும்!
ஆகியவற்றுக்கு இடையே இந்த விகிதமுறு எண்கள் மட்டுமே உள்ளனவா? சிந்திக்கவும்! முடிந்தால் அவற்றிற்கிடையே மேலும் 10 விகிதமுறு எண்களைக் காண முயற்சிக்கவும்!
குறிப்பு
கீழே கொடுக்கப்பட்டுள்ளவாறு, 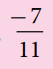 மற்றும்
மற்றும் ![]() ஆகிய விகிதமுறு எண்களுக்கு இடையில் பல விகிதமுறு எண்களை நாம் விரைவாகக் காணலாம்:
ஆகிய விகிதமுறு எண்களுக்கு இடையில் பல விகிதமுறு எண்களை நாம் விரைவாகக் காணலாம்:
திட்ட வடிவ விகிதமுறு எண்களின் வீச்சினை, பகுதிகளைத் தொகுதிகளோடு குறுக்குப் பெருக்கல் செய்து காணலாம்.  ஆனது, குறுக்குப் பெருக்கலில் பகுதியானது 99 ஆக இருக்கும்படியும் வீச்சானது −63 முதல் −55 வரையிலும் கொடுக்கும். இது, கொடுக்கப்பட்ட விகிதமுறு எண்களின் பகுதியானது 99 ஆக இருக்கும்படி சமான விகிதமுறு எண்களை அமைப்பதாகுமே தவிர வேறொன்றுமில்லை!
ஆனது, குறுக்குப் பெருக்கலில் பகுதியானது 99 ஆக இருக்கும்படியும் வீச்சானது −63 முதல் −55 வரையிலும் கொடுக்கும். இது, கொடுக்கப்பட்ட விகிதமுறு எண்களின் பகுதியானது 99 ஆக இருக்கும்படி சமான விகிதமுறு எண்களை அமைப்பதாகுமே தவிர வேறொன்றுமில்லை!