விகிதமுறு எண்களின் பண்புகள்

விகிதமுறு எண்களின் பண்புகள்

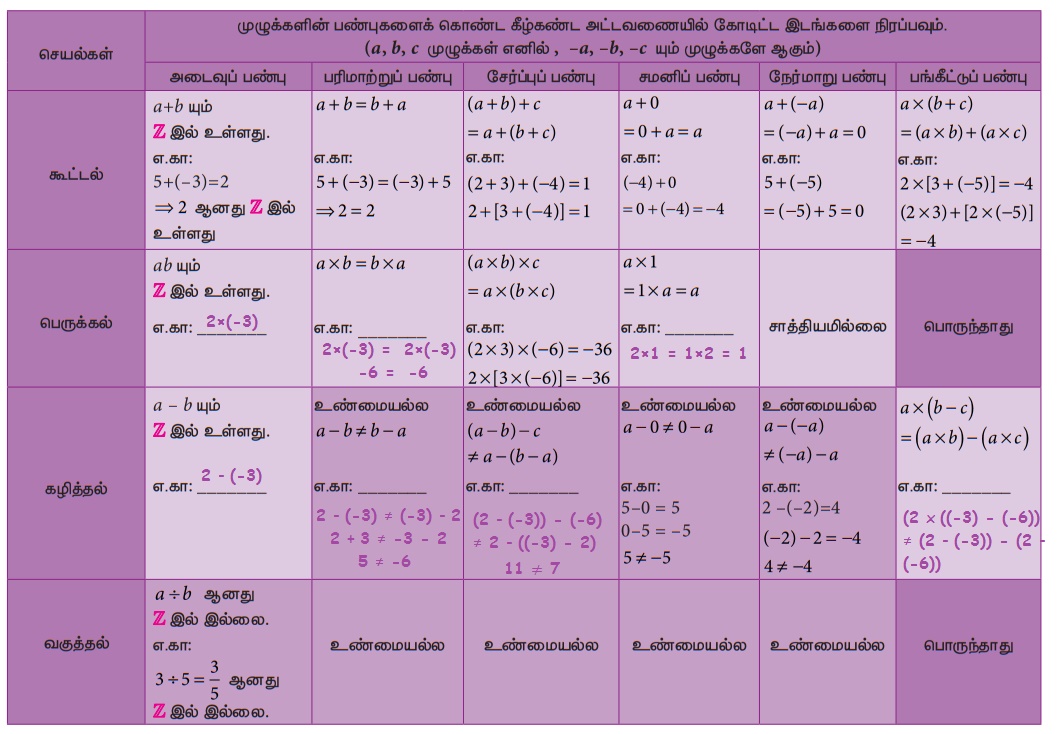
இங்குக் கீழே பட்டியலிடப்பட்டுள்ள சில பண்புகள் கணக்குகளைத் தீர்க்க மிகுந்தப் பயனளிக்கும்.

1. Q என்ற விகிதமுறு எண்களின் தொகுப்பிற்கான அடைவுப் பண்பு/விதி 

i) கூட்டலுக்கான அடைவுப் பண்பு:

a மற்றும் b என்ற ஏதேனும் இரு விகிதமுறு எண்களின் கூடுதலான a + b ஆனதும் ஒரு விகிதமுறு எண்ணாகும். 

ii) பெருக்கலுக்கான அடைவுப் பண்பு:

a மற்றும் b என்ற ஏதேனும் இரு விகிதமுறு எண்களின் பெருக்கல்பலனான ab ஆனதும் ஒரு விகிதமுறு எண்ணாகும்.

விளக்கம்

இவற்றை முயல்க

முழுக்களின் மீதான அடைவுப் பண்பு கழித்தலுக்கு உண்மையாகும் ஆனால் வகுத்தலுக்கு உண்மையல்ல. இது விகிதமுறு எண்களுக்கு என்னவாகும்? சரிபார்க்கவும்.

2. Q என்ற விகிதமுறு எண்களின் தொகுப்பிற்கான பரிமாற்றுப் பண்பு/விதி 

i) கூட்டலுக்கான பரிமாற்றுப் பண்பு:

a மற்றும் b என்ற ஏதேனும் இரு விகிதமுறு எண்களுக்கு a + b = b + a ஆகும். 

ii) பெருக்கலுக்கான பரிமாற்றுப் பண்பு:

a மற்றும் b என்ற ஏதேனும் இரு விகிதமுறு எண்களுக்கு ab = ba ஆகும். (இங்கு ab என்பது a × b மற்றும் ba என்பது b × a ஆகும்.)

விளக்கம்

இங்கு, a + b = b + a என நாம் காண்கிறோம். ஆகவே, கூட்டலானது பரிமாற்றுப் பண்பை நிறைவு செய்கிறது. 

மேலும்,

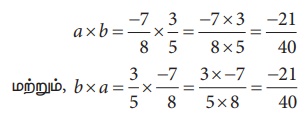
இவற்றை முயல்க 

1. 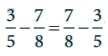 என்பது சரியாகுமா?

2. 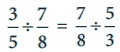என்பது சரியாகுமா?

எனவே, உனது முடிவு என்ன?

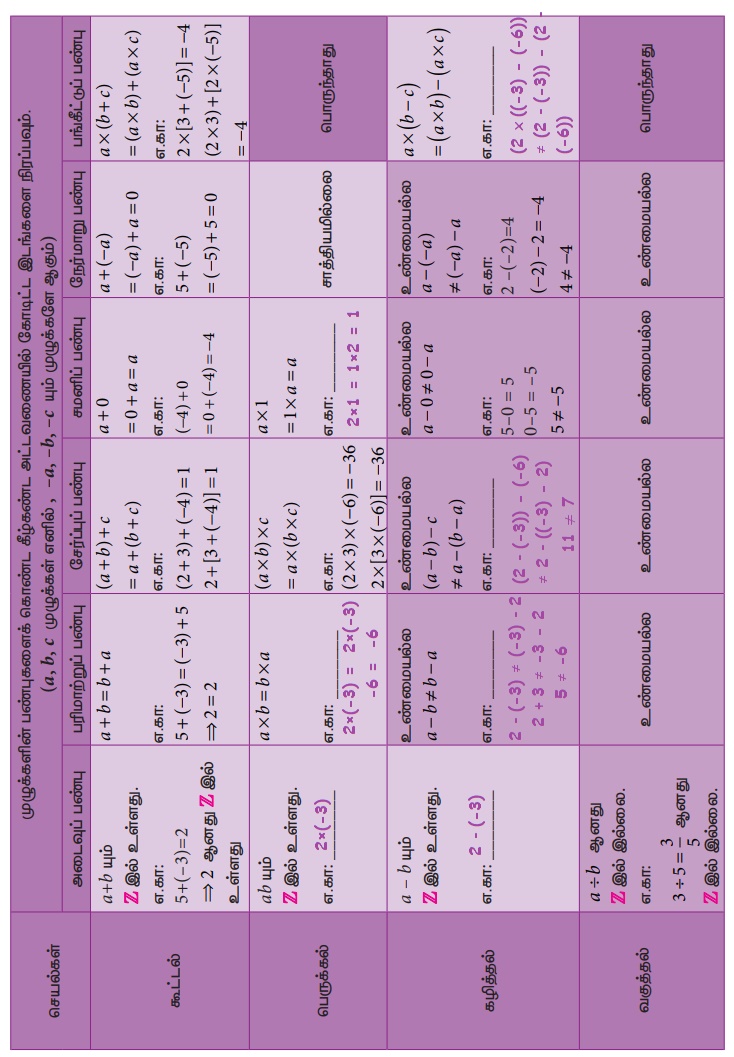
இங்கு, a × b = b × a என நாம் காண்கிறோம். ஆகவே, பெருக்கலானது பரிமாற்றுப் பண்பை நிறைவு செய்கிறது. 

3. Q என்ற விகிதமுறு எண்களின் தொகுப்பிற்கான சேர்ப்பு பண்பு/விதி 

i) கூட்டலுக்கான சேர்ப்பு பண்பு:

a, b மற்றும் c என்ற ஏதேனும் 3 விகிதமுறு எண்களுக்கு, a + (b + c) = (a + b) + c ஆகும். 

ii) பெருக்கலுக்கான சேர்ப்பு பண்பு: 

a, b மற்றும் c என்ற ஏதேனும் 3 விகிதமுறு எண்களுக்கு, a (bc) = (ab) c ஆகும்.

விளக்கம்

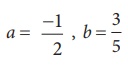மற்றும் 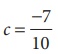என மூன்று விகிதமுறு எண்களை எடுத்துக் கொள்ளவும்.

இங்கு, 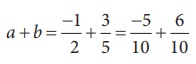(ஒரே பகுதியைக் கொண்ட சமான விகிதமுறு எண்கள்)

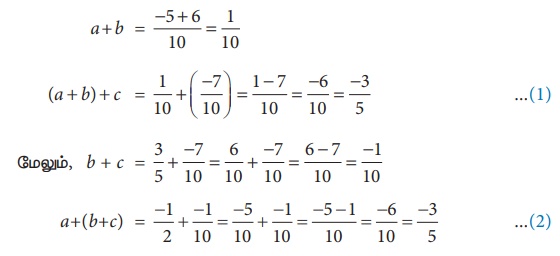
(1) மற்றும்  (2) இலிருந்து, (a + b) + c = a + (b + c) என்பது விகிதமுறு எண்களுக்கு உண்மையாகிறது.

இதுபோன்று, 

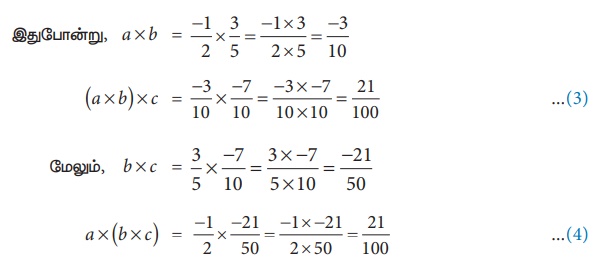
(3) மற்றும் (4) இலிருந்து, (a × b) × c = a × (b × c) என்பது விகிதமுறு எண்களுக்கு உண்மையாகிறது. ஆகவே, விகிதமுறு எண்களுக்கு சேர்ப்புப் பண்பானது கூட்டல் மற்றும் பெருக்கலுக்கு உண்மையாகிறது.

இவற்றை முயல்க

விகிதமுறு எண்களுக்கு, கழித்தல் மற்றும் வகுத்தலானது சேர்ப்புப் பண்பை நிறைவு செய்யுமா? என சரிபார்க்கவும்.

4. Q என்ற விகிதமுறு எண்களின் தொகுப்பிற்கான சமனிப் பண்பு/விதி 

i) கூட்டலுக்கான சமனிப் பண்பு:

a என்ற எந்தவொரு விகிதமுறு எண்ணிற்கும் 0 + a = a = 0 + a என்று அமையுமாறு 0 என்ற தனித்த விகிதமுறு எண்ணானது இருக்கிறது.

ii) பெருக்கலுக்கான சமனிப் பண்பு:

a என்ற எந்தவொரு விகிதமுறு எண்ணிற்கும் 1 × a = a = a × 1 என்று அமையுமாறு 1 என்ற தனித்த விகிதமுறு எண்ணானது இருக்கிறது.

விளக்கம்

5. Q என்ற விகிதமுறு எண்களின் தொகுப்பிற்கான நேர்மாறுப் பண்பு/விதி 

i) கூட்டல் நேர்மாறுப் பண்பு:

a என்ற எந்தவொரு விகிதமுறு எண்ணிற்கும் a + (−a) = (−a) + a = 0 என்று அமையுமாறு −a என்ற தனித்த விகிதமுறு எண் இருக்கும். இங்கு, 0 ஆனது கூட்டல் சமனி ஆகும். 

ii) பெருக்கல் நேர்மாறுப் பண்பு: 

b என்ற எந்தவொரு விகிதமுறு எண்ணிற்கும் 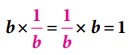என்று அமையுமாறு  என்ற தனித்த விகிதமுறு எண் இருக்கும். இங்கு, 1 ஆனது பெருக்கல் சமனி ஆகும்.

விளக்கம்

6. Q என்ற விகிதமுறு எண்களின் தொகுப்பிற்கான பங்கீட்டுப் பண்பு/விதி

விகிதமுறு எண்களின் தொகுப்பிற்கு, பெருக்கலானது கூட்டலைப் பங்கீடுச் செய்யும்.

a, b மற்றும் c என்ற ஏதேனும் மூன்று விகிதமுறு எண்களுக்கு, a × (b + c ) = (a × b) + (a × c) என்பது பங்கீட்டு விதி ஆகும். 

விளக்கம்:

(1) மற்றும் (2) ஆனது a × (b + c) = (a × b) + (a × c) எனக் காட்டுகிறது.

ஆகவே, Q என்ற விகிதமுறு எண்களின் தொகுப்பிற்கு, கூட்டலின் மீதான பெருக்களின் பங்கீட்டுப் பண்பு உண்மையாகும்.