கனங்களும், கனமூலங்களும்

கனங்களும், கனமூலங்களும்

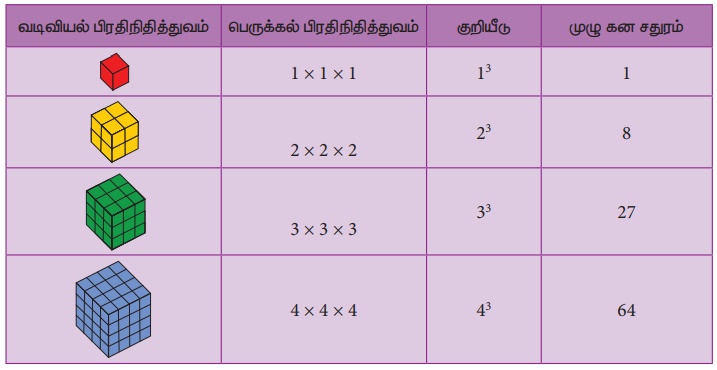
ஓர் எண்ணை அதே எண்ணால் பெருக்கி, மீண்டுமொருமுறை அதே எண்ணால் பெருக்கினால் கிடைப்பது கன எண் ஆகும். அதாவது, மூன்று ஒரே சம எண்களின் பெருக்கல்பலனே அந்த எண்ணின் கன எண் ஆகும். ஓர் எண்ணானது n எனில், அதன் கனத்தை n3 எனக் குறிப்பிடுவோம்.

கன எண்களை, ஓரலகு கனங்களைக் கொண்ட முப்பரிமாணக் கனங்கள் மூலம் காட்சிப்படுத்தி விளக்கலாம். கன எண்களானது முழுக் கனங்கள் என்றும் அழைக்கப்படும். இயல் எண்களின் முழு கனங்களாக 1, 8, 27, 64, 125, 216, ... ஆகிய எண்கள் அமைகின்றன.

உங்களுக்குத் தெரியுமா?

இராமானுஜன் எண் − 1729 = 123 + 13 = 103+ 93 

ஒரு சமயம், நோயுற்றிருந்த கணிதமேதை இராமானுஜனைப் பார்க்க, 1729 என்ற வாடகை மகிழுந்தில் கணித விரிவுரையாளர் ஹார்டி என்பவர், புட்னி என்ற இடத்திற்குப் பயணம் செய்தார். ஹார்டி, இராமானுஜனிடம் அந்த மகிழுந்தின் எண்ணானது மந்தமானதாகவும் சகுணம் சரி இல்லாத எண்ணாக இல்லாமலிருக்க தான் நம்புவதாகவும் கூறினார். அதற்கு இராமானுஜன், "அப்படி இல்லை" என்றவர், தொடர்ந்து "அது, இரு கன எண்களின் கூடுதலாக இரு வழிகளில் எழுத இயலும் மற்றும் ஆர்வத்தைத் தூண்டும் ஓர் மிகச் சிறிய எண்ணாகும்" என்று முடித்தார். இது போலவே 4104, 13832, 20683 ஆகியவை இராமானுஜன்−ஹார்டி எண்களின் எடுத்துக்காட்டுக்கள் ஆகும்.

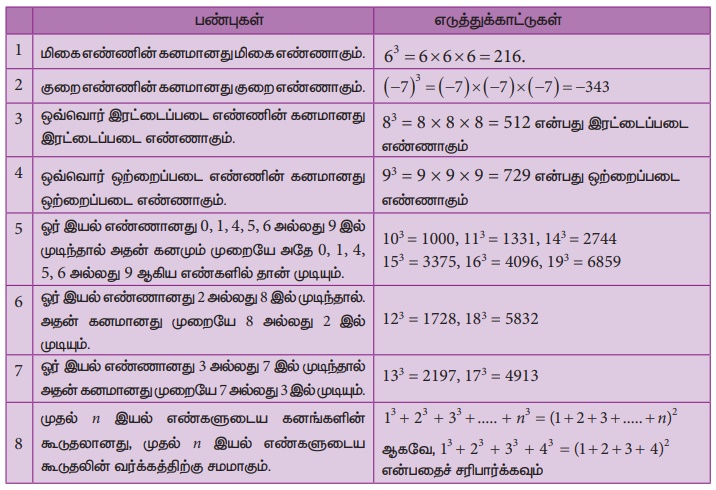
1. எண்களுடைய கனங்களின் பண்புகள் 

குறிப்பு

* ஒரு முழு கனமானது இரண்டு பூச்சியங்களுடன் முடியாது. 

* ஓர் ஈரிலக்க எண்ணின் கனத்தில் 4 அல்லது 5 அல்லது 6 இலக்கங்கள் இருக்க வாய்ப்புண்டு.

இவற்றை முயல்க 

பின்வரும் எண்களின் கனத்திலுள்ள ஒன்றுகள் இலக்கத்தைக் காண்க. 

1. 17 

2. 12 

3. 38 

4. 53 

5. 71 

6. 84

2. கனமூலம்

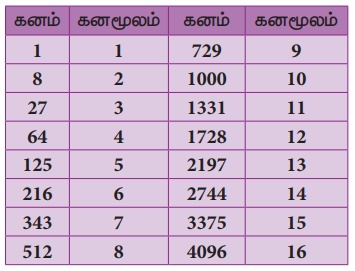
ஒரு மதிப்பின் கனமானது அசல் எண்ணைத் தரும் எனில், அந்த மதிப்பானது அசல் எண்ணின் கனமூலம் எனப்படும். 

எடுத்துக்காட்டாக, 27 இன் கனமூலம் 3 ஆகும். ஏனெனில், 3 இன் கனமானது 27−ஐ தரும். 

குறியீடு: 

ஓர் எண் x இன் கனமூலமானது 3√ x அல்லது x1/3 எனக் குறிக்கப்படுகிறது. 

இங்கு, சில கனங்களும் கனமூலங்களும் கொடுக்கப்பட்டுள்ளன.

3√1 = 1 ஏனெனில், 13 = 1, 3√ 8 = 2 ஏனெனில், 23 = 8, 

3√27 = 3 ஏனெனில், 33 = 27, 3√ 64 = 4 ஏனெனில், 43 = 64, 

3√125 = 5 ஏனெனில், 53 = 125... எனத் தொடர்ந்துக் கொண்டே செல்லும்.

எடுத்துக்காட்டு 1.32

400 என்பது ஒரு முழு கன எண்ணாகுமா? 

தீர்வு :

பகாக் காரணிப்படுத்துதல் மூலம், நாம் 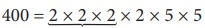எனப் பெறுகிறோம். இங்கு, ஒரே ஒரு மூன்றன் தொகுதி மட்டுமே உள்ளது. மேற்கொண்டு மூன்றன் தொகுதிகளைப் பெற நமக்கு இன்னும் இரண்டு 2களும் ஒரு 5 உம் தேவை. ஆகவே, 400 ஆனது ஒரு முழு கன எண்ணல்ல. 

எடுத்துக்காட்டு 1.33

675 உடன் எந்த மிகச் சிறிய எண்ணைப் பெருக்கினால் ஒரு முழு கன எண்ணைப் பெறலாம்?

தீர்வு:

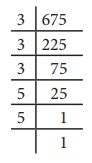
675 = 3 × 3 × 3 × 5 × 5 ............ (1) 

என நாம் பார்க்கிறோம். 675 இன் பகாக் காரணிகளை மூன்றன் தொகுதிகளாகப் பிரித்தால், 5 × 5 மட்டும் மீதமாக இருக்கும். ஆகவே, அதை முழு கன எண்ணாக ஆக்க நமக்கு மேலும் ஒரு 5 தேவை. ஆகவே, 675 ஐ ஒரு முழு கன எண்ணாக மாற்ற (1) இன் இருபுறமும் 5 ஆல் பெருக்க வேண்டும். 

675 × 5 = (3 × 3 × 3 × 5 × 5) × 5 

3375 = 3 × 3 × 3 × 5 × 5 × 5 

இப்போது, 3375 ஆனது ஒரு முழு கன எண்ணாகும். எனவே, 675 ஆனது ஒரு முழு கன எண்ணாக, அதனுடன் பெருக்க வேண்டிய மிகச் சிறிய எண்ணானது 5 ஆகும்.

சிந்திக்க

இந்த வினாவில், 'பெருக்கினால்' என்பதற்கு பதிலாக 'வகுத்தால்' என மாற்றினால், தீர்வு எவ்வாறு மாறுபடும்?

3. பகாக் காரணிப்படுத்துதல் மூலம் ஓர் எண்ணின் கனமூலம் காணுதல் 

படி 1: கொடுக்கப்பட்ட எண்ணை பகாக் காரணிகளின் பெருக்கல்பலனாகப் பிரிக்க வேண்டும். 

படி 2: ஒரே பகாக் காரணிகளைக் கொண்ட மூன்றன் தொகுதிகளை அமைக்க வேண்டும். 

படி 3: ஒவ்வொரு மூன்றன் தொகுதியிலிருந்தும் ஓர் எண்ணைத் தேர்வு செய்து, அந்தப் பகாக் காரணிகளின் பெருக்கல்பலனைக் கண்டு கனமூலத்தைக் பெறலாம். 

எடுத்துக்காட்டு 1.34

27000 இன் கனமூலத்தைக் காண்க. 

தீர்வு : 

பகாக்காரணிப்படுத்துதல் மூலம், நாம் பெறுவது. 27000 = 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5 × 5

ஃ 3√ 27000 = 2 × 3 × 5 = 30

எடுத்துக்காட்டு 1.35