அலகு 1 | 8 ஆம் வகுப்பு கணக்கு - விகிதமுறு எண்ணை தசம எண்ணாக எழுதுதல் | 8th Maths : Chapter 1 : Numbers
8 ஆம் வகுப்பு கணக்கு : அலகு 1 : எண்கள்
விகிதமுறு எண்ணை தசம எண்ணாக எழுதுதல்
2. விகிதமுறு எண்ணை தசம எண்ணாக எழுதுதல்
ஒரு விகிதமுறு எண்ணை வழக்கமான பின்ன வடிவத்தைக் காட்டிலும் அழகாக தசம வடிவத்தில் குறிக்கலாம். கொடுக்கப்பட்ட, 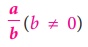 (b ≠ 0) வடிவத்தில் உள்ள ஒரு விகிதமுறு எண்ணில், தொகுதி a ஐ பகுதி b ஆல் சாதாரணமாக வகுக்க அந்த எண்ணை முடிவுறு அல்லது முடிவுறா, தொடரும் தசம எண்ணாக வெளிப்படுத்தலாம் என்பதை நாம் காணலாம்.
(b ≠ 0) வடிவத்தில் உள்ள ஒரு விகிதமுறு எண்ணில், தொகுதி a ஐ பகுதி b ஆல் சாதாரணமாக வகுக்க அந்த எண்ணை முடிவுறு அல்லது முடிவுறா, தொடரும் தசம எண்ணாக வெளிப்படுத்தலாம் என்பதை நாம் காணலாம்.
செயல்பாடு

ஒரு கயிற்றினை எண்கோடாகப் பயன்படுத்தி, வகுப்பறையின் நீளம் முழுக்க அதனை சுவரில் கட்டவும். கயிற்றில் போதுமான இடம் விட்டு முழுக்களைப் பொருத்தவும். பிறகு, மாணவர்களிடம் ஒரு பெட்டியில் உள்ள விகிதமுறு எண் அட்டைகளை எடுக்கச் சொல்லி அவற்றை தோராயமாக சரியான இடத்தில் கயிற்றில் பொருத்த சொல்ல வேண்டும். இந்த விளையாட்டை குழுக்களாக விளையாடச் செய்யலாம். எந்தக் குழு அதிக அட்டைகளை சரியாக கயிற்றின் மீது பொருத்துகிறதோ அந்தக் குழு வெற்றி பெற்றதாகும்.
எடுத்துக்காட்டு 1.1
பின்வரும் விகிதமுறு எண்களை தசம எண்களாக எழுதுக.
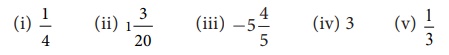
தீர்வு :
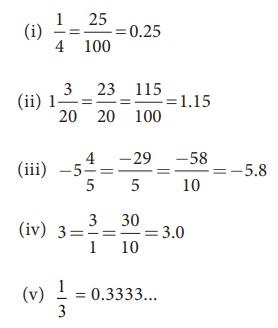
(சரியாக வகுத்துக் கிடைப்பது. மேலும் இது தொடரும் முடிவுறா தசம எண்ணாகும்)
குறிப்பு
• மேற்காணும் எடுத்துக்காட்டுகள் மூலம் ஒரு விகிதமுறு எண்ணை எவ்வாறு தசம வடிவத்தில் எழுதலாம் என்பதைக் காட்டுகின்றன. இதன் எதிர்மறைச் செயல்முறையான தசம வடிவிலிருந்து பின்ன வடிவத்திற்கு மாற்றுதல் குறித்து உயர் வகுப்புகளில் பார்க்கலாம்.
• π = 3.141592653589793238462643....
√2 = 1.41421356237309504880168......
போன்று முடிவுறா மற்றும் மீண்டும் தொடராத தசம எண்களும் உண்டு. இவை விகிதமுறு எண்கள் அல்ல. இவற்றைப் பற்றி கூடுதலாக உயர் வகுப்புகளில் நாம் படிக்கலாம்.
இவற்றை முயல்க
பின்வரும் விகிதமுறு எண்களை தசம எண்களாக எழுதுக.