வர்க்கமூலம்

வர்க்கமூலம்

கூட்டல், கழித்தல், பெருக்கல் போன்ற செயல்பாடுகளைப் போன்றே வர்க்கப்படுத்துதலும் ஒரு கணிதச் செயல்பாடு ஆகும். பெரும்பாலான கணிதச் செயல்பாடுகளுக்கு நேர்மாறு (எதிர்மறை எனப் பொருள்படும்) செயல்பாடுகள் உண்டு. எடுத்துக்காட்டாக, கழித்தலானது, கூட்டலுக்கு நேர்மாறாகவும், வகுத்தலானது, பெருக்கலுக்கு நேர்மாறாகவும் உள்ளன. இவ்வாறே வர்க்கமானது வர்க்கமூலம் காணுதலை ஒரு நேர்மாறு செயல்பாடாக பெற்றுள்ளது.

ஏதேனும் ஒரு n என்ற எண்ணை, இரு ஒரே எண்களின் பெருக்கல்பலன் வழங்கினால் அந்த எண்ணானது n இன் வர்க்கமூலம் எனப்படும். இதனை √n அல்லது n1/2 எனக் குறிக்கலாம். எடுத்துக்காட்டாக √81 என்பது 9 ஆகும். ஏனெனில் 9 × 9 = 81 ஆகும். அருகிலுள்ள அட்டவணையில், 1 முதல் 100 வரையிலான அனைத்து முழு வர்க்க எண்களின் வர்க்கமூலங்கள் கொடுக்கப்பட்டுள்ளன.

112 = 121 எனில், √121 என்பது யாது? 529 = 232 எனில், 529 இன் வர்க்கமூலம் யாது? நமக்கு, 324 = 182 எனத் தெரியுமானால், உடனடியாக நாம் √324 = 18 எனக் கூறிவிடலாம்.

இங்கு, 12 = 1 ஆகும். ஆகவே, 1 இன் வர்க்கமூலம் 1 ஆகும். மேலும் (−1)2 = 1 ஆகும். ஆகவே, −1 ஆனதும் 1 இன் வர்க்கமூலம் ஆகும்.

22 = 4 ஆகும், ஆகவே 4 இன் வர்க்கமூலம் 2 ஆகும். மேலும் (−2)2 = 4 ஆகும். ஆகவே, −2 ஆனதும் 4 இன் வர்க்கமூலம் ஆகும். இது போன்று, 32 = 9 ஆகும். ஆகவே 9 இன் வர்க்கமூலம் 3 ஆகும். மேலும் (−3)2 = 9 ஆகும். ஆகவே 9 இன் வர்க்கமூலம் 3 மற்றும் −3 எனத் தொடர்கிறது.

மேற்காணும் எடுத்துக்காட்டுகள், ஒரு முழு வர்க்க எண்ணிற்கு, வர்க்கமூலங்களாக இரு முழுக்கள் இருப்பதைத் தெரிவிக்கின்றன. ஆனால், கணக்குகளில் நாம் ஓர் இயல் எண்ணின் மிகை வர்க்கமூலத்தையே எடுத்துக்கொள்வோம். ஓர் எண்ணின் மிகை வர்க்க மூலத்தை எப்போதும் √ என்ற குறியீடைக் கொண்டு குறிக்கப்படுகிறது.

ஆகவே, √4 என்பது 2 மட்டுமே (−2 அல்ல). மேலும், √9 என்பது 3 மட்டுமே (−3 அல்ல). இது பொதுவாக ஒப்புக் கொள்ளப்பட்ட குறியீடாகும் என்பதனை நாம் நினைவில் கொள்ள வேண்டும். 

1. பகாக்காரணிப்படுத்துதல் மூலம் வர்க்கமூலம் காணுதல்

எண்களின் பகாக்காரணிகளையும் அந்த எண்களின் வர்க்கங்களின் பகாக்காரணிகளையும் கொண்ட பின்வரும் அட்டவணையைக் கவனிக்க.

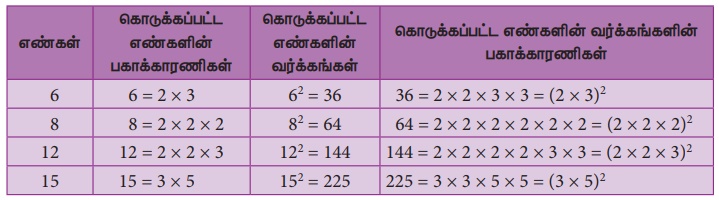
6 மற்றும் அதன் பகாக்காரணிகளைக் கவனிக்கவும். இதில் 2 மற்றும் 3 ஆனது எத்தனை முறை பட்டியலில் வருகின்றன? இப்போது, அதன் வர்க்கமான 36 மற்றும் அதன் பகாக்காரணிகளைக் கவனிப்போம். இங்கு, 2 மற்றும் 3 ஆனது எத்தனை முறை வருகின்றன? இவ்வாறே 8, 12 மற்றும் 15 ஆகிய எண்களுக்கும் கண்டுபிடிக்கவும். (நாம் நமது விருப்பம் போல் எந்த ஓர் எண்ணையும் அதன் வர்க்கத்தையும் தேர்ந்தெடுக்கலாம்) நாம் காண்பது என்ன? நாம் காண்பது யாதெனில்,

ஓர் எண்ணின் வர்க்கத்தில் உள்ள பகாக்காரணிகளின் எண்ணிக்கை = அந்த எண்ணின் பகாக்காரணிகளின் எண்ணிக்கையைப் போன்று இரு மடங்கு என்பதாகும்.

இந்தக் கருத்தைப் பயன்படுத்தி நாம் ஒரு முழு வர்க்க எண்ணின் வர்க்கமூலத்தைக் காணலாம். முதலில், கொடுக்கப்பட்ட எண்ணை அதன் பகாக் காரணிகளைக் கொண்டு பிரிக்கவும். ஒரே பகாக் காரணிகளைச் சோடியாகி, அவற்றுள் ஒரு எண்ணை மட்டும் எடுத்து வர்க்கமூலத்தைக் காண வேண்டும்.  

எடுத்துக்காட்டு 1.22

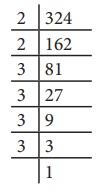
பகாக் காரணிபடுத்துதல் முறையில் 324 இன் வர்க்கமூலத்தைக் காண்க. 

தீர்வு:

முதலில், கொடுக்கப்பட்ட எண்ணை அதன் பகாக் காரணிகளைக் கொண்டு பிரிக்கவும். ஒரே பகாக் காரணிகளைச் சோடியாக்கி, அவற்றுள் ஒரு எண்ணை மட்டும் எடுத்து வர்க்கமூலம் காண வேண்டும். 

இங்கு, 324 = 2 × 2 × 3 × 3 × 3 × 3 

= 22 × 32 × 32

= (2 × 3 × 3)2 

ஃ √324 = √(2 × 3 × 3)2

= 2 × 3 × 3 

= 18

எடுத்துக்காட்டு 1.23

250 ஐ எந்த மிகச் சிறிய எண்ணால் பெருக்கவோ வகுக்கவோ அது ஒரு முழுவர்க்க எண்ணாகும் எனக் காண்க. மேலும், அதன் வர்க்கமூலத்தைக் காண்க. 

தீர்வு : 

இங்கு, 250 = 5 × 5 × 5 × 2 = 52 × 5 × 2 

இங்கு, பகாக் காரணிகளான 5 மற்றும் 2 இக்கு சோடிகள் இல்லை. 

எனவே, நாம் 250 ஐ 10 (5 × 2) ஆல் பெருக்கவோ, வகுக்கவோ செய்யலாம்.

(i) 250 ஐ 10 ஆல் பெருக்க, நாம் பெறுவது 2500 = 52 × 5 × 2 × 5 × 2. ஆகவே, 2500 இன் வர்க்கமூலம் 5 × 5 × 2 = 50 ஆகும். 

(ii) 250 ஐ 10 ஆல் வகுக்க, நாம் பெறுவது 25. இங்கு √25 = √52 = 5 எனப் பெறுகிறோம்.

எடுத்துக்காட்டு 1.24

108 ஆனது ஒரு முழு வர்க்க எண்ணாகுமா? 

தீர்வு : 

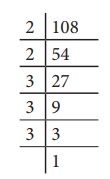
இங்கு, 108 = 2 × 2 × 3 × 3 × 3

= 22 × 32 × 3

இங்கு, பகாக்காரணியான 3 இக்கு இரண்டாவது சோடி இல்லை. ஆகவே, 108 ஆனது ஒரு முழு வர்க்க எண் அல்ல.

சிந்திக்க

இங்கு, 108 ஐப் பெருக்கி அல்லது வகுத்து ஒரு முழு வர்க்க எண்ணாக்க, மிகச்சிறிய  காரணியைக் காண வேண்டும் எனில், நாம் என்ன செய்ய வேண்டும்?

2. நீள் வகுத்தல் முறையில் ஓர் எண்ணின் வர்க்கமூலத்தைக் காணுதல்

அதிகப்படியான இலக்கங்களைக் கொண்ட எண்களை நாம் காணும்போது, அவற்றின் வர்க்கமூலங்களைப் பகாக்காரணிப்படுத்துதல் முறையில் காண்பது என்பது நீளமானதாகவும் கடினமானதாகவும் அமையக்கூடும். அவ்வாறான சூழல்களில், நீள் வகுத்தல் முறையைப் பயன்படுத்துவது நமக்கு உதவிடும். இந்த முறையைப் பற்றி நாம் இரண்டு விளக்கங்களைக் கொண்டு இங்கு பார்க்கலாம். 

விளக்கம் 1

நீள் வகுத்தல் முறையில் 576 இன் வர்க்கமூலத்தைக் காண்க. 

படி 1: 

ஒன்றுகள் இடத்தில் உள்ள இலக்கம் தொடங்கி, இலக்கங்களைச் சோடியாக்கவும் ஒவ்வொரு சோடியும், மீதமுள்ள இலக்கமும் (ஏதேனும் இருப்பின்) ஒரு காலக் கட்டம் எனப்படும். ஒவ்வொரு சோடியின் மீதும் ஒரு சிறுக்கோட்டுத்துண்டினை இடவும் (கொடுக்கப்பட்ட எண்ணின் வலதுப் புறத்திலிருந்து). அந்த எண்ணில் ஒற்றை எண்ணிக்கையிலான இலக்கங்கள் இருப்பின், இடதுப்புற கடைசி இலக்கத்தின் மீது சிறுக்கோட்டுத்துண்டு இருக்காது.

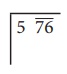
ஆகவே, இங்கு நமக்கு 5 என உள்ளது. 

படி 2: 

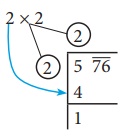
முதல் காலக் கட்டத்திலுள்ள எண்ணை விடச் சமமாகவோ அல்லது குறைவாகவோ உள்ள மிகப் பெரிய எண்ணின் வர்க்கத்தைச் சிந்திக்கவும். அந்த எண்ணை வகுத்தியாகவும் ஈவு ஆகவும் எடுத்துக்கொள்ளவும். இங்கு, கடைசி இடதுப்புற எண் 5 ஆகும். ஆகவே, 5 இக்குச் சமமாகவோ அல்லது குறைவாகவோ உள்ள மிகப் பெரிய எண்ணின் வர்க்கமானது 2 ஆகும். இதுவே, நமது வகுத்தியும் ஈவும் ஆகும். 

படி 3: 

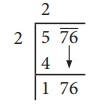
76 ஐ கீழே கொண்டு வந்து, மீதிக்கு வலதுபுறமாக எழுதவும். இப்போது, புதிய வகுபடும் எண்ணாக 176 ஆனது கிடைக்கும்.

படி 4:

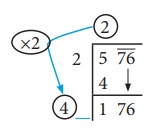
புதிய வகுத்தியைக் காண, முன்பு பெற்ற ஈவு (2) ஐ 2 ஆல் (எப்போதும்) பெருக்க வேண்டும். மேலும், அதனருகே ஒரு சிறு இடத்தை விட்டு விட வேண்டும்.

படி 5:

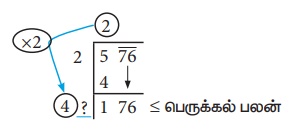
இங்கு புதிய வகுத்தியான 4 உடன் ஓர் இலக்கம் சேரும். புதிய ஈவுடன் புதிய வகுத்தியைப் பெருக்கினால் அது 176 ஐ விடக் குறைவாகவோ அல்லது சமமாகவோ இருக்கும்படி இந்த இலக்கத்தைத் தேர்வு செய்ய வேண்டும்.

படி 6: 

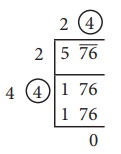
தேவையான இலக்கமாக இங்கு 4 அல்லது 6 ஆக இருக்கும் எனத் தெளிவாகிறது. (ஏன்?) ஆனால் நாம் கணக்கிடும்போது, 46 × 6 = 276 ஆகவும் 44 × 4 = 176 ஆகவும் கிடைக்கிறது. ஆகவே, அந்தச் சிறு இடத்தில் 4 என்ற எண்ணை இடுக்கிறோம். இங்கு 176 இலிருந்து 176 ஐ எழுதிக் கழித்து 0 ஐ மீதியாகப் பெறுகிறோம். அதாவது, மேலே உள்ள 24 என்ற ஈவானது 576 இன் வர்க்கமூலம் ஆகும்.

ஃ √576 = 24 ஆகும்.

விளக்கம் 2

பின்வரும் எடுத்துக்காட்டில், 288369 இன் வர்க்கமூலத்தை ஒவ்வொரு நிலையிலும் காணுதலும் படிவாரியாக கணக்கிடுதலும் கொடுக்கப்பட்டுள்ளது. ஒவ்வொரு படியையும் ஒன்றன் பின் ஒன்றாகக் கவனித்து, அந்த படிகள் விளக்குவதைப் புரிந்துகொள்ளவும்.

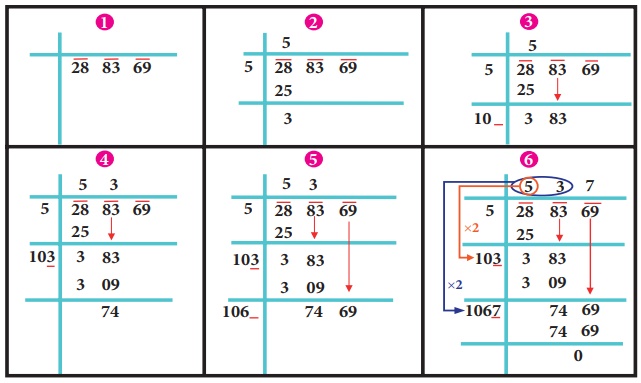
நாம் √288369 = 537 எனக் காண்கிறோம். 

எடுத்துக்காட்டு 1.25

நீள் வகுத்தல் முறையில் 459684 இன் வர்க்கமூலத்தைக் காண்க. 

தீர்வு :

நீள் வகுத்தல் முறையில் 459684 இன் வர்க்கமூலத்தை நாம் கீழே கொடுக்கப்பட்டுள்ளவாறுக் காணலாம்.

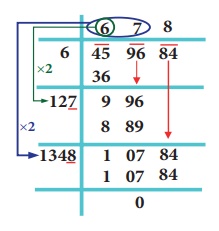
ஃ √459684 = 678

எடுத்துக்காட்டு 1.26

ஒரு சதுர நிலத்தின் பரப்பளவு 3136 சதுர மீட்டர் எனில், அதன் சுற்றளவைக் காண்க.

தீர்வு :

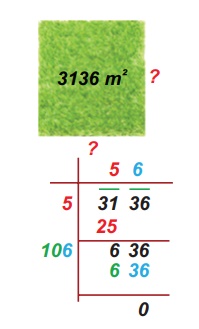
சதுர நிலத்தின் பரப்பு = 3136 மீ2 (தரவு) 

ஃ சதுர நிலத்தின் பக்க அளவு = √3136 = 56 மீ 

ஃ சதுர நிலத்தின் சுற்றளவு = 4 × பக்க அளவு

= 4 × 56 

= 224 மீ

எடுத்துக்காட்டு 1.27

மனையின் சொந்தக்காரர் ஒருவர், 39 மீ பக்க அளவுக் கொண்ட ஒரு சதுர மனையும், 100 மீ நீளமும் 64 மீ அகலமும் கொண்ட ஒரு செவ்வக மனையும் என 2 மனைகள் வைத்திருந்தார். இவை இரண்டையும் விற்று, அவர் புதியதாக அதே பரப்பளவில் ஒரு சதுர மனையை வாங்குகிறார் எனில், அவருடைய புதிய சதுர மனையின் பக்க அளவு என்ன? 

தீர்வு :

பரிமாற்றங்களைப் பின்வருமாறு காணலாம்:

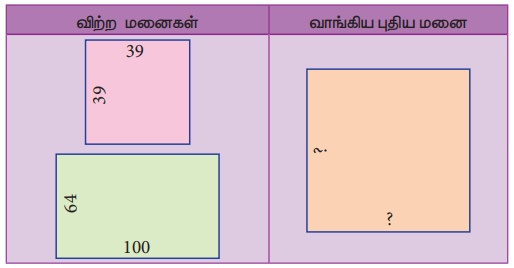
வாங்கிய சதுர மனையின் பரப்பளவு = விற்ற சதுர மனையின் பரப்பளவு + விற்ற செவ்வக மனையின் பரப்பளவு 

= (39 × 39) + (100 × 64)

= 1521 + 6400

= 7921 மீ 

புதிய சதுர மனையின் பக்க அளவு = √7921 = 89 மீ

இவற்றை முயல்க 

நீள் வகுத்தல் முறையில் வர்க்க மூலத்தைக் காண்க. 

1. 400 

2. 1764 

3. 9801

3. ஒரு முழு வர்க்க எண்ணின் வர்க்கமூலத்திலுள்ள இலக்கங்களின் எண்ணிக்கையைக் காணுதல்

நீள் வகுத்தல் முறையில், வர்க்கமூலத்தைக் காண நாம் சிறுக்கோட்டுத்துண்டினைப் பயன்படுத்தினோம். இந்தக் சிறுக்கோட்டுத்துண்டுக் குறிகள், ஒரு முழு வர்க்க எண்ணின் வர்க்கமூலத்தில் உள்ள இலக்கங்களின் எண்ணிக்கையைக் காண உதவும். பின்வரும் எடுத்துக்காட்டுகளைக் கவனிக்கவும் (நீள் வகுத்தல் முறையில் சிறு கோட்டுத்துண்டுகளுடன் வர்க்கமூலத்தைக் காணும் போது)

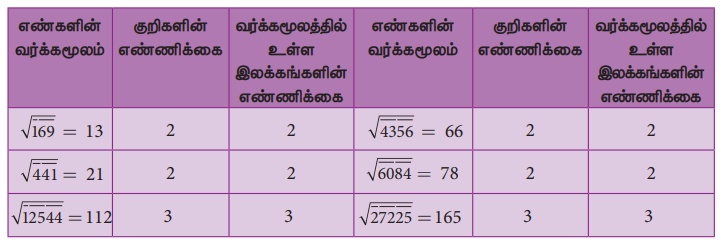
ஆகவே, சிறுக்கோட்டுத்துண்டுகளின் எண்ணிக்கையானது வர்க்கமூலத்திலுள்ள இலக்கங்களின் எண்ணிக்கையைக் குறிக்கும் என நாம் முடிவு செய்கிறோம்.

இவற்றை முயல்க

வர்க்கமூலத்தைக் கணக்கிடாமல், பின்வரும் எண்களின் வர்க்கமூலத்திலுள்ள இலக்கங்களின் எண்ணிக்கையை ஊகித்துக் கூறவும். 

1. 14400 

2. 390625 

3. 100000000

4. தசம எண்களின் வர்க்கமூலத்தைக் காணுதல்

தசம வடிவிலுள்ள எண்களின் வர்க்கமூலத்தைக் கணக்கிட நாம் பின்வரும் படிகளைப் பின்பற்றுவோம்.

படி 1:

தசம இடங்கள் இரட்டையாக வரும்படி தசமப் பகுதியிலுள்ள கடைசி இலக்கத்திற்கு அடுத்து பூச்சியத்தைச் சேர்க்க வேண்டும் (தேவைப்பட்டால் மட்டுமே). 

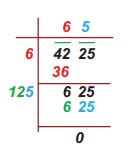
√42.25 ஐக் காணுதல்

படி 2: 

கொடுக்கப்பட்ட எண்ணில் முழுக்களின் பகுதியும் தசமப் பகுதியும் உள்ளன. முழுக்கள் பகுதியை, முன்பு செய்ததுப் போன்று சிறு கோட்டுத்துண்டினை இட்டு, நீள் வகுத்தல் முறையைப் பயன்படுத்திக் கண்டவாறு முழு வர்க்க எண்ணின் வர்க்கமூலத்தைக் காண வேண்டும்.

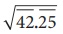இல் சிறுக்கோட்டுத்துண்டுகளை நாம் இடுகிறோம்.

படி 3: 

தசமப் பகுதியில், முதல் தசம் இடத்தில் தொடங்கிச் சோடி எண்களுக்குச் சிறு கோட்டுத்துண்டினை இட வேண்டும்.

படி 4: 

இப்போது, நீள் வகுத்தல் முறையில் வர்க்கமூலத்தைக் காண வேண்டும். 

படி 5: 

முழுக்கள் பகுதி முடிந்தவுடன், தசமப் புள்ளியை வர்க்கமூலத்தில் இட வேண்டும்.

ஃ √42.25 = 6.5

இவற்றை முயல்க: 1. 5.4756 2. 19.36 3. 116.64 ஆகியவற்றின் வர்க்கமூலத்தைக் காண்க.

5. எண்களின் பெருக்கல் மற்றும் வகுத்தல் ஆகியவற்றின் வர்க்கமூலத்தைக் காணுதல்

ஏதேனும் இரு மிகை எண்கள் a மற்றும் b இக்கு, 

(i) √[ab] = √a × √b 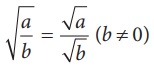 மற்றும் (ii) 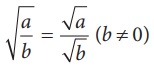ஆகும்.

எடுத்துக்காட்டு 1.28

√256 இன் மதிப்பைக் காண்க. 

தீர்வு : 

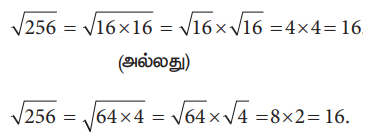
√256 = √(16 × 16) = √16 × √16 = 4 × 4 = 16 (அல்லது)

√256 = √(64 × 4) = √64 × √4 = 8 × 2 = 16.

சிந்திக்க

√[ab] = √a × √b ஐப் பயன்படுத்தி கோடிட்ட இடங்களை நிரப்ப முயற்சிக்கவும்:

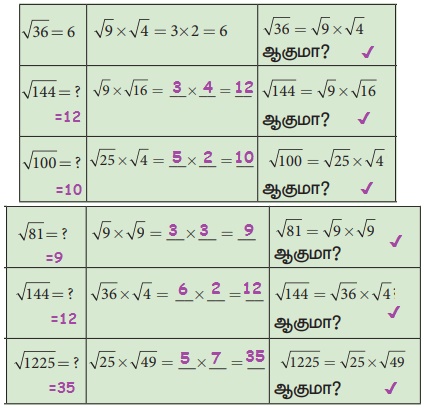
செயல்பாடு

மேற்கண்ட அட்டவணையைப் போன்று, a மற்றும் b ஆகிய இரு முழு வர்க்க எண்களுக்கு 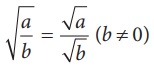ஆனது நிறைவு செய்யும்படி வர்க்கமூலக் கணக்குகளைக் கொண்ட ஓர் அட்டவணையைத் தயாரிக்க. இந்தச் சிந்தனையைப் பயன்படுத்திக் குறிப்பிட்ட சில வர்க்கமூலக் கணக்குகளை எளிதில் கணக்கிட முடியும்.

எடுத்துக்காட்டு 1.29

√42.25 இன் மதிப்பைக் காண்க. 

தீர்வு :

இதனை நாம், 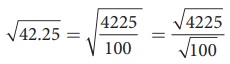என எழுதலாம். 

இப்போது, 4225 என்ற முழு எண்ணின் வர்க்கமூலத்தை நீள் வகுத்தல் முறையில் எளிதாகக் கணக்கிட முடியும்.

√4225 = 65 ஆகவே, நாம் பெறுவது

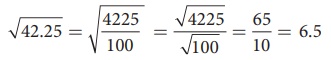
இந்த முறையானது, தசம இடங்களைப் பற்றிக் கவலையில்லாமல், தசம எண்களின் வர்க்கமூலத்தை காணப் பயன்படும் மற்றொரு வழியாக அமைகிறது.

இவற்றை முயல்க

மேற்கண்ட முறையைப் பயன்படுத்தி 1.2321 மற்றம் 11.9025 ஆகிய எண்களின் வர்க்க மூலத்தைக் காண்க. 

எடுத்துக்காட்டு 1.30

குறிப்புரை: 

(ii) கணக்கில், ஒருவரால் உடனடியாக விடையை என கூறிவிடத் தோன்றும். ஆனால், அது தவறாகும். ஏனெனில், கொடுக்கப்பட்ட கலப்பு பின்னத்தைத் தகா பின்னமாக மாற்றிய பிறகு 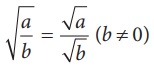என்ற விதியைப் பயன்படுத்தி மட்டுமே விடையைக் கூற வேண்டும்.

6. வர்க்கமூலங்களின் தோராய மதிப்பறிதல் 

கொடுக்கப்பட்டுள்ள √40, 6 மற்றும் 7 ஆகிய எண்களை உங்களால் ஏறுவரிசையில் எழுத இயலுமா? இங்கு 40 என்பது ஒரு வர்க்க எண் அல்ல. அதனால், இதன் வர்க்க மூலத்தை நாம் எளிதாக தீர்மானிக்க இயலாது. ஆனால், √40 இன் தோராய மதிப்பை ஊகிக்க முடியும். அதைக் கணித்து இங்கு பயன்படுத்தலாம்.

√40 இன் தோராய மதிப்பை ஊகிக்க முடியும். அதைக் கணித்து இங்கு பயன்படுத்தலாம்.

40 இன் மிக அருகிலுள்ள இரு வர்க்க எண்களாக 36 மற்றும் 49 ஆகிய எண்கள் இருப்பதை நாம் அறிவோம்.

ஆகவே, 36 < 40 < 49 என்பதை 62 < 40 < 72 என எழுதலாம். 

வர்க்கமூலத்தை காண, நாம் பெறுவது 6 < √40 < 7.

இவற்றை முயல்க 

எண்களை ஏறு வரிசையில் எழுதவும். 

1. 4, √14, 5 மற்றும் 

2. 7, √65, 8