எண்கள்

இயல் 1

எண்கள்

கற்றல் நோக்கங்கள்

* பின்னங்களிலிருந்து விகிதமுறு எண்களுக்கான நீட்டிப்பின் தேவையைப் புரிந்துகொள்ளுதல், விகிதமுறு எண்களை எண்கோட்டின் மீது குறித்தல் மற்றும் கொடுக்கப்பட்ட இரு விகிதமுறு எண்களுக்கிடையே பல விகிதமுறு எண்கள் உள்ளன என அறிதல். 

* விகிதமுறு எண்களின் மீதான நான்கு அடிப்படை கணிதச் செயல்பாடுகளை கற்று, அவற்றைப் பயன்படுத்தி வார்த்தைக் கணக்குகளைத் தீர்த்தல் மற்றும் அதிகபட்சம் மூன்று அடைப்புக்குறிகள் வரையுள்ள கோவைகளைச் சுருக்குதல். 

* விகிதமுறு எண்களின் மீதான பண்புகளைப் புரிந்துகொள்ளுதல். 

* எண்களின் வர்க்கம், வர்க்கமூலம், கனம் மற்றும் கனமூலத்தைக் காணுதல்.

* வர்க்கமூலம் மற்றும் கனமூலத்தின் தோராய மதிப்புகளைக் கணித்தல். 

* எண்களை அடுக்குக் குறியீட்டில் அமைத்தல் மற்றும் முழுக்களைப் படிகளாகக் கொண்ட அடுக்கு விதிகளைப் புரிந்து கொள்ளுதல். 

* எண்களை அறிவியல் குறியீட்டில் அமைத்தலும் அறிதலும்.

அறிமுகம்

நாம் ஏற்கனவே முந்தைய வகுப்புகளில் கற்ற பல விதமான எண்களை நினைவு கூர்வோம். நாம், எண்ண வேண்டும் என விரும்பினால், இயற்கையாகவே 1, 2, 3, 4, 5, என தொடங்குவோம் அல்லவா?

இவையனைத்தும் எண்ணும் எண்கள் அல்லது இயல் எண்கள் எனப்படும். இவற்றின் தொகுப்பானது ℕ எனக் குறிக்கப்படுகிறது. இந்த பட்டியலின் இறுதியில் வைக்கப்பட்டுள்ள மூன்று புள்ளிகள், இந்த பட்டியலானது எப்போதும் தொடர்ந்துக் கொண்டே செல்லும் என்பதைக் குறிப்பதாகும்.

இந்த எண்களைக் குறிக்கப்பெற்ற ஒரு கதிரின் மூலமாக இயல் எண்களைக் காணலாம்.

நேற்று எனது பணப்பையில் ₹8 ரொக்கமாக இருந்தது என்ற சூழலைக் கருத்தில் கொள்வோம். ஆனால், இன்று பணப்பையானது காலியாக இருக்கலாம். ஆகவே, இப்போது பணப்பையில் எவ்வளவு ரூபாய் உள்ளது? இந்த வெறுமையை எவ்வாறு குறிப்பது? இங்கு தான் பூச்சியத்தின் கருத்தானது வெறுமையின் கருத்தைக் குறிப்பிட உருவானது. பூச்சியத்தின் கருத்தானது தற்போது இயல்பாகவே ஏற்றுக் கொள்ளப்பட்ட ஒன்று என்றாலும் கூட, அது முற்காலத்திய மனிதர்களுக்கு சாதாரணமான ஒன்றாக இருக்கவில்லை. பல நூறு ஆண்டுகளுக்குப் பிறகே, மக்கள் அதை உண்மையில் ஒரு எண்ணாக நினைக்கத் தொடங்கினர். இந்திய கணிதவியலாளர்கள் பூச்சியத்திற்கான குறியீட்டை அளித்தவுடன் இந்த இன்னலானது தீர்ந்தது. இந்த இயல் எண்கள் அமைப்பானது பூச்சிய எண்ணை கூடுதலாக சேர்த்தவுடன் முழு எண்கள் ஆகின.

இப்போது முழு எண்களை பின்வருமாறு கற்பனைச் செய்துப் பார்க்கலாம்.

முழு எண்களின் அமைப்பானது W எனக் குறிக்கப்படுகிறது. 

பூச்சியம் கூட எல்லாக் கணக்குகளையும் தீர்க்க போதுமானதாக அமையவில்லை. 6 இலிருந்து 4ஐ எடுத்தால் என்ன நடக்கும்? எனச் சிந்திக்கவும்.

9 வரையிலான ஓர் எண்கோட்டை வரையவும், அதன் மீது 6 ஐ ஒரு புள்ளியாகக் குறிக்கவும்.

4 ஐ கழிக்க, நாம் 6 இலிருந்து இடதுபுறமாக 4 படிகள் செல்ல வேண்டும் என்பது நமக்குத் தெரியும். நாம் 2 ஐ அடைந்து விடையானது 2 எனக் கிடைக்கிறது. ஆனால், இப்போது நாம் 4 இலிருந்து 6 ஐக் கழிக்க வேண்டுமெனில், என்ன ஆகும்? இந்த சூழல் தான் மனிதர்களுக்கு குறை எண்கள் தேவையும்பட்டது (உருவாக்கவும்பட்டது).

ஆனால், ஓர் எண்ணானது எப்படி குறையாக இருக்க முடியும்? எளிது!  அவற்றை பூச்சியத்தை விட குறைவானவை என நினைத்துக் கொண்டால் போதும். குறை முழுக்களை முழு எண்களோடு சேர்க்க நமக்கு முழுக்கள் பட்டியல் கிடைக்கிறது. முழுக்களானது, பூச்சியம், இயல் எண்கள் மற்றும் இயல் எண்களின் எதிர்மறைகளையும் கொண்டு எதிரெதிர் திசைகளிலும் முடியாமல் நீளும் எண்களின் பட்டியலைக் கொண்டதாகும். முழுக்களின் மொத்த தொகுப்பானது ℤ எனக் குறிக்கப்படுகிறது.

எங்கும் கணிதம் − அன்றாட வாழ்வில் எண்கள்

ஓர் ஆரஞ்சு பழமானது உரிக்கப்பட்டு அதனுள் 8 சுளைகள் காணப்பட்டால், ஒரு சுளையானது என்ற விகிதமுறு எண்ணைக் குறிக்கும்.

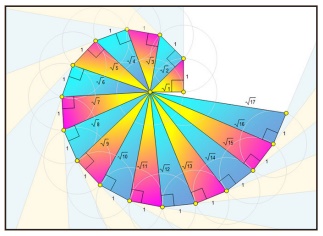
வடிவியலில் உள்ள பிதாகரஸ் தோற்றத்தைப் பயன்படுத்தி சுருள் வடிவில் எண்களின் வர்க்கமூலத்தைக் காணுதல்.