அடுக்குக்குறிகளும் படிகளும்

அடுக்குக்குறிகளும் படிகளும்

சில எண்களை எவ்வாறு வர்க்கங்களாகவும், கனங்களாகவும் எழுதலாம் என்பது நமக்குத் தெரியும். எடுத்துக்காட்டாக, 25 ஐ 52 எனவும் 125 ஐ 53 எனவும் எழுதுவோம்.

பொதுவாக, ஒரே காரணியின் தொடர் பெருக்கலைக் குறிக்கும் ஒரு கோவையை நாம் படி (Power) என்கிறோம். இங்கு, எண் 5 ஆனது அடிமானம் (Base) எனப்படும். எண் 2 ஆனது அடுக்கு (Exponent) எனப்படும் (இது வழக்கத்தில் பெரும்பாலும் படி என்றே அழைக்கப்படுகிறது). அடுக்கு என்பது ஓர் அடிமான எண்ணானது எத்தனை முறை காரணியாகப் பயன்படுத்தப்படுகிறது என்பதை குறிப்பதாகும்.

1. மிகை அடுக்குகளைக் கொண்ட படிகள்

முழு எண்களை அடுக்குகளாகக் கொண்ட படிகளின் மதிப்பானது எப்போதும் விரைவாகக் கூடிக் கொண்டே செல்லும் பின்வரும் எடுத்துக்காட்டினைக் கவனிக்க.

21 = 2 

22 = 2 × 2 = 4

23 = 2 × 2 × 2 = 8

24 = 2 × 2 × 2 × 2 = 16

25 = 2 × 2 × 2 × 2 × 2 = 32

26 = 2 × 2 × 2 × 2 × 2 × 2 = 64

27 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128

28 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256

29 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2  = 512

210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024

இதே வேகத்தில், 2100 இன் மதிப்பு என்னவாக இருக்கும் என நீ நினைக்கிறாய்? 

இங்கு 2100 = 1267650600228229401496703205376 ஆகும். 

ஆகவே, நாம் பெரிய எண்களை எதிர்கொள்ளும்போது முழு எண்களை அடுக்குகளாகக் கொண்ட அடுக்குக் குறியீடானது பயனுள்ளதாக அமைகிறது என புரிந்து கொள்ளலாம். 

2. பூச்சியமும் குறை அடுக்குகளைக் கொண்ட படிகளும்

இந்த அமைப்பைக் கவனிக்க. ஆரம்பம் முதல் கொண்டு, அடுத்தடுத்த படிகளில் என்ன நடக்கிறது? முடிவானது முந்திய படியின் மதிப்பில் பாதியாக இருப்பதைப் பார்க்கிறோம் அல்லவா. ஆகவே, 20 பற்றி நாம் என்ன கூறலாம்? 

இதே போன்று 35, 34, 33 என அவற்றிற்கு ஓர் அட்டவணையைத் தயாரித்தால், அதிலிருந்து 30 பற்றி நாம் அறிவது யாது?

அதற்கு 2 இன் அமைப்பைப் பயன்படுத்தி, எந்தவொரு பூச்சியமற்ற எண்ணின் பூச்சிய அடுக்கானது 1 என்பதை நாம் காணலாம்.

a0 = 1, இங்கு a ≠ 0

இந்த அமைப்பை மேலும் நீட்டிப்புச் செய்தால் என்ன நடக்கிறது என்பதைப் பார்ப்போம். முன்பு போலவே, ஆரம்பம் முதல் கொண்டு அடுத்தடுத்த படிகளின் முடிவானது முந்தைய படியின் மதிப்பில் பாதியாக இருப்பதைக் காண்கிறோம். 

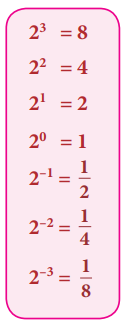
20 = 1 என்பதால், அடுத்தப் படியான 2−1 இன் மதிப்பானது முந்தைய படியின் மதிப்பினை 2 ஆல் வகுக்கக் கிடைப்பதாகும். அதாவது, ஆகும். அடுத்ததாக 2−2 இன் மதிப்பானது ஐ 2 ஆல் வகுக்க கிடைப்பது ஆகும். அதாவது ஆகும். இவ்வாறாக இது தொடரும்.

பொதுவாக,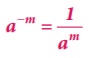 இங்கு m ஆனது ஒரு முழு எண் ஆகும்.

3. அடுக்குகளைப் பயன்படுத்தி எண்களின் விரிவாக்க அமைப்பைக் காணுதல்

கீழ் வகுப்புகளில், ஒரு முழு எண்ணை எவ்வாறு விரிவாக்கம் செய்து எழுதலாம் என்பதை கற்று இருக்கிறோம். எடுத்துக்காட்டாக, 

5832 = (5 × 1000) + (8 × 100) + (3 × 10) + (2 × 1)

= (5 × 103) + (8 × 102) + (3 × 101) + 2 (நாம் அடுக்குக் குறியீட்டைப் பயன்படுத்தும் போது)

தசமப் புள்ளியில் எண்கள் தரப்பட்டால் அவற்றின் விரிவாக்கத்தை நாம் எப்படிச் செய்வது? இங்கு 10 இன் குறை அடுக்குகள் நமக்கு உதவிடும்!

ஆகவே,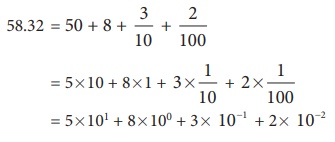

இவற்றை முயல்க

அடுக்குகளைப் பயன்படுத்தி பின்வரும் எண்களை விரிவாக்கம் செய்க.  

1. 8120 

2. 20305

3. 3652.01 

4. 9426.521 

4. அடுக்குகளின் விதிகள்

குறிப்பிட்ட அடிப்படை கருத்துக்களைக் கொண்டு அமைவனவே அடுக்குகளின் விதிகள் ஆகும். ஒரு மிகை அடுக்கானது நாம் ஓர் எண்ணை, பெருக்கலில் எத்தனை முறை பயன்படுத்துகிறோம் என்பதைக் குறிப்பதாகும். ஆனால், ஒரு குறை அடுக்கானது ஓர் எண்ணை, எத்தனை முறை வகுக்கப் பயன்படுத்துகிறோம் என்பதைக் குறிப்பதாகும். ஏனெனில், பெருக்கலின் நேர்மாறு வகுத்தலாகும். 

பெருக்கல் விதி

இந்த விதியின்படி, ஒரே அடிமான எண்களைக் கொண்ட இரண்டு படி எண்களைப் பெருக்கும்போது, நாம் அதன் அடுக்குகளைக் கூட்டிக் கொள்ளலாம். அதாவது,

am × an = am+n 

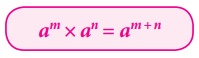
இங்கு, a  (a ≠ 0), m, n என்பது முழுக்கள் ஆகும். இங்கு, அடிமான எண்கள், இரண்டு படி எண்களிலும் சமமாக இருக்க வேண்டும் என்பதைக் கவனிக்கவும். 

எடுத்துக்காட்டுகள் : 

வகுத்தல் விதி

இந்த விதியின்படி, ஒரே அடிமான எண்களைக் கொண்ட இரண்டு படி எண்களை வகுக்கும் போது நாம் அதன் அடுக்குகளைக் கழித்துக் கொள்ளலாம். அதாவது, 

இங்கு, a  (a ≠ 0), m, n என்பன முழுக்கள் ஆகும். இங்கு, அடிமான எண்கள், இரண்டு படி எண்களிலும் சமமாக இருக்க வேண்டும் என்பதைக் கவனிக்கவும்.

இது எவ்வாறு உண்மையாகிறது என்பதைப் பின்வரும் எடுத்துக்காட்டுகள் மூலம் அறியலாம்.

எடுத்துக்காட்டுகள்:

படி விதி

இந்த விதியின்படி, ஒரு படி எண்ணை மற்றொரு அடுக்கிற்கு உயர்த்தினால், நாம் அந்த அடுக்குகளைப் பெருக்கிக் கொள்ளலாம்.

(am)n = amn 

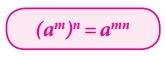
இங்கு a (a ≠ 0), m, n என்பன முழுக்கள் ஆகும் 

எடுத்துக்காட்டுகள்: 

விதியின்படி [(−2)3]2 = (−2)3×2 = (−2)6 = 64

அல்லது 

[(−2)3]2 = [(−2) × (−2) × (−2)]2 = [−8]2 = 64

இவற்றை முயல்க

பின்வரும் விதிகளைச் சரிபார்க்க (மேலே செய்தது போன்று). இங்கு, a, b என்பன பூச்சியமற்ற முழுக்கள் எனவும் m, n ஆகியன முழுக்கள் எனவும் கொள்க. 

1. ஒரே படிகளைக் கொண்ட இரு எண்களின் பெருகல்பலன் அந்த எண்களின் பெருக்கல்பலனின் படிக்குச் சமம் என்ற விதி : am × bm = (ab)m. 

2. ஒரே படிகளைக் கொண்ட இரு எண்களின் வகுத்தலானது அந்த எண்களின் வகுத்தலின் படிக்குச் சமம் என்ற விதி :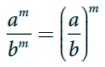

3. பூச்சிய அடுக்கு விதி : a0 = 1.

எடுத்துக்காட்டு 1.36

எடுத்துக்காட்டு 1.38

(−7)x+2 × (−7)5 = (−7)10 எனில் x ஐக் காண்க. 

தீர்வு : 

(−7)(x + 2) × (−7)5 = (−7)10 

(−7)(x + 2 + 5) = (−7)10

இங்கு அடிமான எண்கள் சமம். ஆகவே, அடுக்குகளை சமன் செய்து நாம் பெறுவது,

x + 7 = 10  

⇒ x = 10 −7 = 3

5. திட்டக் குறியீடும் அறிவியல் குறியீடும்

ஓர் எண்ணின் திட்டக் குறியீடு (வடிவம்) என்பது ஓர் எண்ணை நாம் வழக்கமாக எழுதுவதே ஆகும். நாம், ஓர் எண்ணின் ஒவ்வொரு இலக்கத்தின் மதிப்பைக் காண்பிக்க விரிவாக்கக் குறியீட்டைப் பயன்படுத்துகிறோம். அதாவது, அந்த எண்ணை ஒவ்வொரு இலக்கத்தின் இடமதிப்பைக் கொண்டு பொருத்தி (ஒன்றுகள், பத்துகள், நூறுகள்... போன்று) அதனை ஒவ்வொரு இலக்கத்தின் கூடுதலாக எழுதுகிறோம்.

எடுத்துக்காட்டாக, 195 ஆனது திட்டவடிவில் உள்ளது. அதனை, 195 = (1 × 100) + (9 × 10) + (5 × 1) என விரிவாக்கம் செய்யலாம்.

வானியலாளர்கள், உயிரியலாளர்கள், பொறியாளர்கள், இயற்பியலாளர்கள் என பலர் மிகச் சிறிய மற்றும் மிகப் பெரிய எண்களை அளவுகளாகக் கொண்ட பொருள்களை அவ்வப்போது எதிர் நோக்குகிறார்கள். அவர்கள், அவற்றைத் திட்டக் குறியீட்டில் எழுதினால், மற்றவர்களுக்கு எளிதாகப் புரியவோ அல்லது கணக்கிடவோ அமையாது. இவ்வாறான எண்களை எளிமையாகப் புரிந்துக் கொள்ளவும் கணக்கிடவும் ஒரு வழியாக நமக்கு அறிவியல் குறியீடு உதவுகிறது.

அறிவியல் குறியீட்டில் எழுத S × 10a என்ற வடிவத்தைப் பின்பற்ற வேண்டும். இங்கு S ஆனது 1 இக்கும் 10 இக்கும் (முழுக்கள் அல்லது தசம எண்கள்) இடையே உள்ள ஓர் எண்ணாகும். அது 10 ஆக இருக்கக்கூடாது. மேலும், a ஆனது ஒரு மிகை அல்லது குறை முழு ஆகும்.

ஓர் எண்ணை அறிவியல் குறியீட்டில், ஓர் எண்ணுடன் (முழுக்கள் அல்லது தசம எண்கள்) 10 இன் படியாகப் பெருக்கிக் காட்டுவதாகும். நாம் தசமத்தை (தசம புள்ளி) 1 இலிருந்து 9 க்குள் ஓர் எண் கிடைக்கும் வரை முன்பாகவோ அல்லது பின்னோக்கியோ நகர்த்தி செல்ல வேண்டும். தசமப் புள்ளியை முன்பாகவோ அல்லது பின்னோக்கியோ எத்தனை இடங்கள் நகர்த்தினோம் என்பதை வைத்து, 10 இன் படியை கூட்ட வேண்டும். 

எடுத்துக்காட்டுக்கள்: 

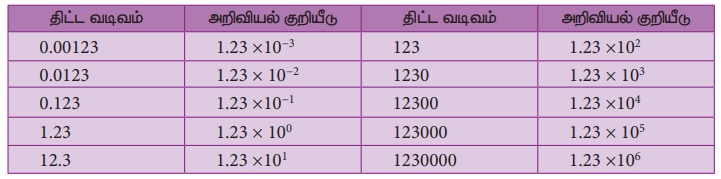
மேலும் சில எடுத்துக்காட்டுகள்: 

(அ) பூமியின் விட்டமானது 12756000 மைல்கள் ஆகும், இதனை அறிவியல் குறியீட்டில் 1.2756 × 107 மைல்கள் என எழுதலாம். 

(ஆ) வியாழன் கிரகத்தின் கன அளவு என்பது சுமார் 143,300,000,000,000 கி.மீ3 ஆகும். இதனை அறிவியல் குறியீட்டில் 1.433 × 1014 கி.மீ3 என எளிதாக எழுதலாம். 

(இ) பாக்டீரியாவின் அளவு 0.00000085 மி.மீ. இதனை, அறிவியல் குறியீட்டில் 8.5 × 10−7 மி.மீ என எளிதாக எழுதலாம்.

குறிப்பு

1. 1.3 × 1012 இல் உள்ள மிகை அடுக்கானது, அந்த எண்ணானது பெரியது எனக் குறிக்கிறது. 

2. 7.89 × 10−21 இல் உள்ள குறை அடுக்கானது, அந்த எண்ணானது சிறியது எனக் குறிக்கிறது. 

எடுத்துக்காட்டு 1.39

அறிவியல் குறியீடுகளை ஒன்று சேர்க்க: 

(i) (7 × 102) (5.2 × 107) 

(ii) (3.7 × 10−5) (2 × 10−3) 

தீர்வு :

(i) (7 × 102) (5.2 × 107) = 36.4 × 109 = 3.64 × 1010 

(ii) (3.7 × 10−5) (2 × 10−3) = 7.4 × 10−8

எடுத்துக்காட்டு 1.40

திட்ட வடிவில் எழுதுக: 

(i) 2.27 × 10−4 

(ii) ஒளியானது ஒரு வினாடிக்கு 1.86 × 105 மைல்கள் வேகத்தில் செல்லும். 

தீர்வு:

(i) 2.27 × 10−4 = 0.000227. 

(ii) ஒளியானது வினாடிக்கு 1.86 × 105 மைல்கள் என்ற வேகத்தில் செல்லும் = 186000 மைல்கள் என்ற வேகத்தில் செல்லும்.

இவற்றை முயல்க

1. திட்டக் குறியீட்டில் எழுதுக: யுரேனஸ் கிரகத்தின் எடை 8.68 × 1025 கி.கி ஆகும். 

2. அறிவியல் குறியீட்டில் எழுதுக: 

(i) 0.000012005 

(ii) 4312.345 

(iii) 0.10524 

(iv) சூரியனுக்கும் சனி கிரகத்திற்கும் இடையேயுள்ள தூரம் 1.4335 × 1012 மைல்கள் ஆகும்.