Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї | Я«ЁЯ«▓Я«ЋЯ»Ђ 5 | 8 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«џЯ«░Я»ЇЯ«хЯ«џЯ«« Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї | 8th Maths : Chapter 5 : Geometry
8 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 5 : Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї
Я«џЯ«░Я»ЇЯ«хЯ«џЯ«« Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
1. Я«џЯ«░Я»ЇЯ«хЯ«џЯ«« Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї PQR Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ABC Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я««Я»Ї (РЅА) Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«њЯ«цЯ»ЇЯ«ц Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«њЯ«цЯ»ЇЯ«ц Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я««Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ PQ=AB, QR=BC, PR=AC Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаP = РѕаA, РѕаQ = РѕаB, РѕаR = РѕаC Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕ Я«еЯ«ЙЯ««Я»Ї РѕєPQR РЅА РѕєABC Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
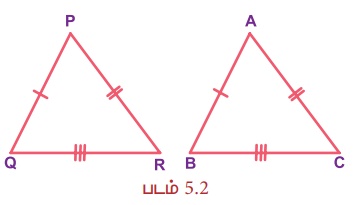
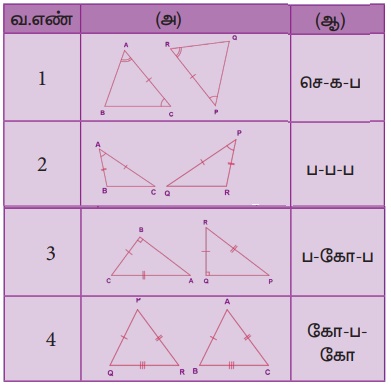
Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ 4 Я«хЯ«┤Я«┐Я«ЋЯ«│Я»Ї Я«ЅЯ«БЯ»ЇЯ«ЪЯ»Ђ. Я«ЁЯ«хЯ»ѕЯ«»Я«ЙЯ«хЯ«Е:
(i) Я«фРѕњЯ«фРѕњЯ«ф (Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Рѕњ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Рѕњ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї) Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»ЇЯ«фЯ«БЯ»ЇЯ«фЯ»Ђ

Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«џЯ«░Я»ЇЯ«х Я«џЯ««Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, AB = PQ, BC = QR, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї AC = PR Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
РЄњ РѕєABC РЅА РѕєPQR.
(ii) Я«фРѕњ Я«ЋЯ»ІРѕњЯ«ф (Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Рѕњ Я«ЋЯ»ІЯ«БЯ««Я»Ї Рѕњ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї) Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»ЇЯ«фЯ«БЯ»ЇЯ«фЯ»Ђ
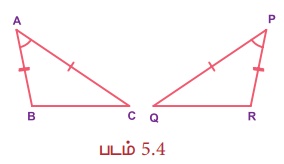
Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«ЁЯ«хЯ»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«ЋЯ»ІЯ«БЯ««Я»ЂЯ««Я»Ї, Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ«хЯ»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«џЯ««Я««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«џЯ«░Я»ЇЯ«х Я«џЯ««Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ AC = PQ, РѕаA = РѕаP Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї AB = PR Я«єЯ«ЋЯ«хЯ»Є, РѕєACB РЅА РѕєPQR.
(iii) Я«ЋЯ»ІРѕњЯ«фРѕњЯ«ЋЯ»І (Я«ЋЯ»ІЯ«БЯ««Я»ЇРѕњЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»ЇРѕњЯ«ЋЯ»ІЯ«БЯ««Я»Ї) Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»ЇЯ«фЯ«БЯ»ЇЯ«фЯ»Ђ
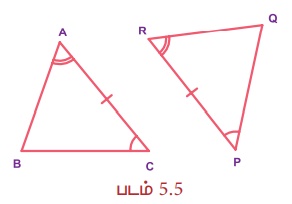
Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»ЂЯ««Я»Ї, Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«џЯ«░Я»ЇЯ«хЯ«џЯ«« Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ РѕаA = РѕаR, CA=PR Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаC = РѕаP, Я«єЯ«ЋЯ«хЯ»Є, РѕєABC РЅА РѕєRQP
(iv) Я«џЯ»єРѕњЯ«ЋРѕњЯ«ф (Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Рѕњ Я«ЋЯ«░Я»ЇЯ«БЯ««Я»Ї Рѕњ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї) Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»ЇЯ«фЯ«БЯ»ЇЯ«фЯ»Ђ
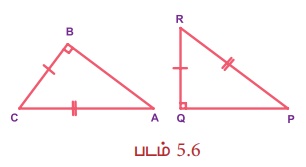
Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ«░Я»ЇЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЁЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ, Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ«░Я»ЇЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЁЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ РѕаB = РѕаQ = 90┬░ (Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї) , BC = QR (Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї AC = PR (Я«ЋЯ«░Я»ЇЯ«БЯ««Я»Ї). Я«єЯ«ЋЯ«хЯ»Є, РѕєABC РЅА РѕєPQR.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Рђб Я«јЯ«еЯ»ЇЯ«цЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї, Я«ЋЯ»ІЯ«БЯ««Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ«цЯ»ЂЯ«хЯ»Є Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ, Я«фЯ«┐Я«░Я«цЯ«┐Я«фЯ«▓Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Рђб Я«ЄЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«њЯ«цЯ»ЇЯ«ц Я«фЯ«ЙЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ CPCTC (Corresponding parts of Congruent Triangles are Congruent) Я«фЯ«БЯ»ЇЯ«фЯ»Ђ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Рђб РђюЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї" Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«│Я»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Рђб "Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї" Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«│Я»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я««Я»ЂЯ«»Я«▓Я»ЇЯ«Ћ
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ«хЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«Ћ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.1
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«фЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»єЯ«░Я«┐Я«»Я«ЙЯ«ц Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
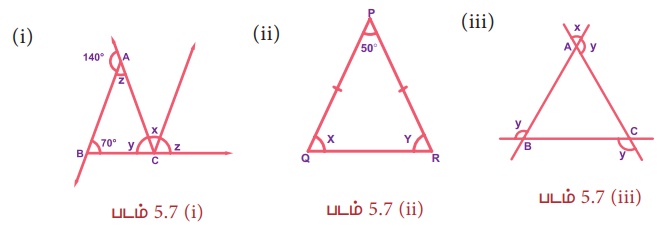
(i) Я«фЯ«ЪЯ««Я»Ї 5.7 (i) Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, 140┬░ + z = 180┬░ (Я«еЯ»ЄЯ«░Я«┐Я«»Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«Б Я«ЄЯ«БЯ»ѕЯ«ЋЯ«│Я»Ї)
РЄњ z = 180┬░ Рѕњ140┬░ = 40┬░
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, x + z = 70┬░ + z (Я«хЯ»єЯ«│Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ)
РЄњ x = 70┬░
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, z + y + 70┬░ = 180┬░ (РѕєABC Я«ЄЯ«▓Я»Ї, Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ)
РЄњ 40┬░ + y + 70┬░ = 180┬░
РЄњ y = 180┬░ Рѕњ 110┬░ = 70┬░
(ii) Я«фЯ«ЪЯ««Я»Ї 5.7 (ii) Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ PQ = PR
РЄњ РѕаQ = РѕаR (Я«џЯ«« Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї)
РЄњ x = y
РЄњ x + y + 50┬░ = 180┬░ (РѕєPQR Я«ЄЯ«▓Я»Ї, Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ)
РЄњ 2x = 130┬░
РЄњ x = 65┬░
РЄњ y = 65┬░
(iii) Я«фЯ«ЪЯ««Я»Ї 5.7 (iii) Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ РѕєABC Я«ЄЯ«▓Я»Ї, РѕаA = x (Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»єЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї)
Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ, РѕаB = РѕаC = x (Я«ЈЯ«ЕЯ»Ї?)
РЄњ РѕаA + РѕаB + РѕаC =180┬░ ( РѕєABC Я«ЄЯ«▓Я»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«фЯ«БЯ»ЇЯ«фЯ»Ђ)
РЄњ 3x = 180┬░
РЄњ x = 60┬░
РЄњ y = 180┬░ Рѕњ 60┬░ = 120┬░
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.2
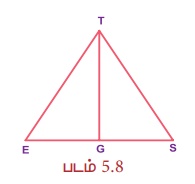
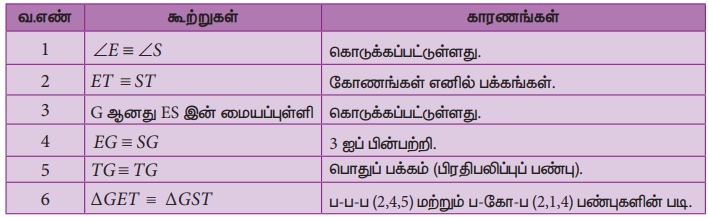
(Я«фРѕњЯ«фРѕњЯ«ф Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фРѕњЯ«ЋЯ»ІРѕњЯ«ф Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ) Я«фЯ«ЪЯ««Я»Ї 5.8 Я«ЄЯ«▓Я»Ї, РѕаE = РѕаS Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ES Я«ЄЯ«ЕЯ»Ї Я««Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ G Я«јЯ«ЕЯ«┐Я«▓Я»Ї, РѕєGET РЅА РѕєGST Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї:
Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«Ћ
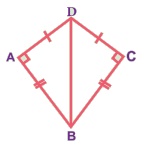
Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї DA = DC Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї BA = BC. Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї DBA Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї DBC Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«џЯ«░Я»ЇЯ«х Я«џЯ««Я««Я«Й? Я«ЈЯ«ЕЯ»Ї?
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.3
(Я«ЋЯ»ІРѕњЯ«фРѕњЯ«ЋЯ»І Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ ) Я«фЯ«ЪЯ««Я»Ї 5.9 Я«ЄЯ«▓Я»Ї, РѕаYTB РЅА РѕаYBT Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаBOY РЅА РѕаTRY Я«јЯ«ЕЯ«┐Я«▓Я»Ї, РѕєBOY РЅА РѕєTRY Я«јЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐.
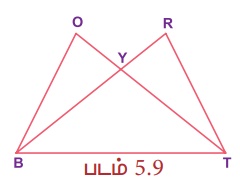
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї:

Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.4
(Я«џЯ»єРѕњЯ«ЋРѕњЯ«ф Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ)
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
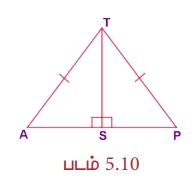
TAP Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЊЯ«░Я»Ї Я«ЄЯ«░Я»ЂЯ«џЯ««Я«фЯ«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, TA = TP Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаTSA = 90┬░ Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
(i) РѕєTAS РЅА РѕєTPS Я«єЯ«ЋЯ»ЂЯ««Я«Й? Я«ЈЯ«ЕЯ»Ї?
(ii) РѕаP = РѕаA Я«єЯ«ЋЯ»ЂЯ««Я«Й? Я«ЈЯ«ЕЯ»Ї?
(iii) AS = PS Я«єЯ«ЋЯ»ЂЯ««Я«Й ? Я«ЈЯ«ЕЯ»Ї?
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї:
(i) TA=TP Я«ЋЯ«░Я»ЇЯ«Б Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаTSA = 90┬░
TS Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Е Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї
Я«єЯ«ЋЯ«хЯ»Є, Я«џЯ»єРѕњЯ«ЋРѕњЯ«ф Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ«ЪЯ«┐, РѕєTAS РЅА РѕєTPS .
(ii) TA=TP Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ
Я«јЯ«ЕЯ«хЯ»Є, РѕаP = РѕаA (Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї)
(iii) (i) Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ РѕєTAS РЅА РѕєTPS,
CPCTC Я«фЯ«БЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ«ЪЯ«┐, AS = PS
Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»єЯ«░Я«┐Я«»Я»ЂЯ««Я«Й?
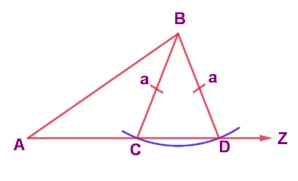
Я«ЄЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ«░Я»ЇЯ«х Я«џЯ««Я««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«░Я»ЂЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«фРѕњЯ«фРѕњЯ«ЋЯ»І Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ІРѕњЯ«фРѕњЯ«ф Я«єЯ«ЋЯ«┐Я«» Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ»ІЯ«цЯ»ЂЯ««Я«ЙЯ«ЕЯ«хЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«хЯ«цЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«ЄЯ«цЯ»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї ABD Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ABC Я«ЄЯ«▓Я»Ї, BC = BD = a Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї AB Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаBAZ Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«ЕЯ«хЯ»ѕ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, AC РЅа AD. Я«єЯ«ЋЯ«хЯ»Є, РѕєABD Я«єЯ«ЕЯ«цЯ»Ђ РѕєABC Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я»ЇЯ«хЯ«џЯ««Я««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓. Я«јЯ«ЕЯ«хЯ»Є, Я«фРѕњЯ«фРѕњЯ«ЋЯ»І Я«фЯ«БЯ»ЇЯ«фЯ»Ђ Я«фЯ»ІЯ«цЯ»ЂЯ««Я«ЙЯ«ЕЯ«цЯ«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«хЯ«цЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ.