நாற்கரங்கள் வரைதல்

நாற்கரங்கள் வரைதல்

முக்கோணங்கள் வரையும் முறையை நாம் ஏற்கனவே கற்றிருக்கிறோம். மூன்று பக்கங்கள் கொண்டு உருவாக்கப்படும் பலகோணம் முக்கோணம் ஆகும். ஒரு முக்கோணம் வரைவதற்கு ஒன்றுக்கொன்று தொடர்பற்ற மூன்று அளவுகள் தேவை. மேலும், மூன்று  பக்கங்கள் கொண்டு ஒரு முக்கோணம் வரையும் போது, ஒரேயொரு வாய்ப்பு மட்டும் உள்ளது. உதாரணமாக, 3 செ.மீ, 5 செ.மீ. மற்றும் 7 செ.மீ. ஆகிய பக்கங்களைக் கொண்டு ஒரு முக்கோணத்தை வரைவதற்கு ஒரேயொரு வாய்ப்பு மட்டுமே உள்ளது.

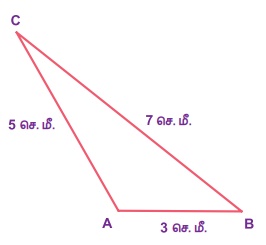
இப்போது, நாற்கரங்களை எடுத்துக்கொள்வோம். நாற்கரமானது நான்கு பக்கங்களால் உருவாக்கப்படும் ஒரு பலகோணம் அல்லவா! ஆனால், நான்கு பக்கங்களைக் கொண்டு நாற்கரம் வரைந்தால் அவை ஒன்றாக இல்லாமல், வெவ்வேறான வடிவில் இருக்கலாம். உதாரணமாக 4 செ.மீ, 5 செ.மீ, 7 செ.மீ. மற்றும் 9 செ.மீ. ஆகிய பக்க அளவுகளைக் கொண்டு வரையப்பட்ட சில நாற்கரங்கள் கீழே கொடுக்கப்பட்டுள்ளன.

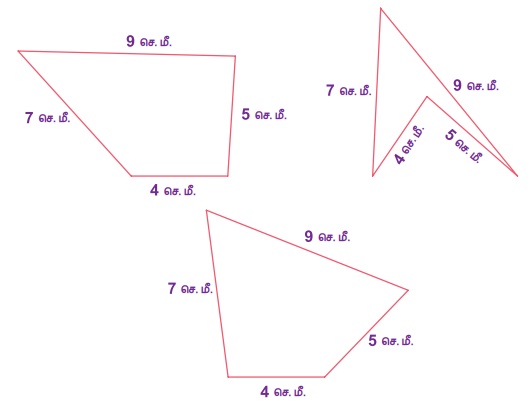
எனவே, ஒரு குறிப்பிட்ட நாற்கரம் வரைவதற்கு, 5−ஆவதாக மற்றொரு அளவு தேவைப்படுகிறது. அது மூலைவிட்டமாகவோ அல்லது கோணமாகவோ இருக்கலாம். அதுமட்டுமின்றி நான்கு பக்கங்களில் 2 அல்லது 3 பக்கங்கள் கொடுக்கப்பட்டிருந்தாலும், மூலைவிட்டங்கள் மற்றும் கோணங்களைப் பயன்படுத்தி நாற்கரங்களை வரைய இயலும்.

குறிப்பு

ஒரு மூலைவிட்டத்தை வரைவதன் மூலம் எந்தவொரு நாற்கரத்தையும் இரண்டு முக்கோணங்களாக நம்மால் பிரிக்க இயலும். 

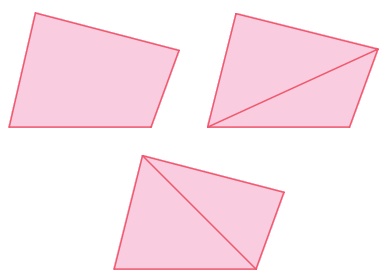
படத்தில், ஒரு நாற்கரமானது அதன் மூலைவிட்டங்களால் இரண்டு வழிகளில் பிரிக்கப்பட்டுள்ளது. எனவே, ஒரு மூலைவிட்டம் கொடுக்கப்பட்டால், இரண்டு பக்கங்கள் மற்றும் அந்த மூலைவிட்டம் ஆகிய அளவுகளைக் கொண்டு கீழ்ப்புறத்தில் உள்ள முக்கோணத்தை முதலில் வரைய வேண்டும். பிறகு, மற்ற இரண்டு அளவுகளைக் கொண்டு மேற்புற முக்கோணத்தை வரைவதன் மூலம் தேவையான நாற்கரத்தைப் பெறலாம்.

உங்களுக்குத் தெரியுமா?

i) • ஒரு பலகோணத்தின் ஏதேனும் ஒரு உட்கோணம் 180o இக்கு அதிகமாக இருந்தால், அது குழிவுப் பலகோணம் ஆகும். கொடுக்கப்பட்ட பலகோணத்தில், உட்கோணம் C ஆனது 180°ஐ விட அதிகமாக உள்ளது. 

• ஒரு பலகோணத்தின் அனைத்து உட்கோணங்களும் 180°ஐ விடக் குறைவாக இருந்தால், அது குவிவுப் பலகோணம் ஆகும். கொடுக்கப்பட்ட பலகோணத்தில், அனைத்து உட்கோணங்களும் 180°ஐ விடக் குறைவாக உள்ளன. 

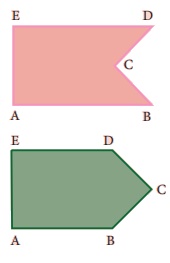
(ii) பின்வரும் நாற்கரங்களை கவனிக்க.

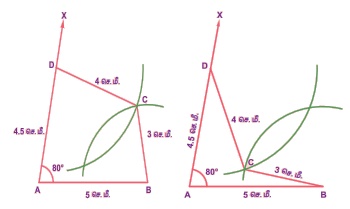
படத்தில் உள்ளவாறு, ஒத்த அளவுகளைக் கொண்டு இரண்டு வகையான நாற்கரங்களை வரைய முடிந்தாலும், இந்த இயலில் குழிவு நாற்கரங்கள் கணக்கில் எடுத்துக் கொள்ளப்படவில்லை. எனவே, குவிவு நாற்கரங்கள் மட்டுமே இங்கு கொடுக்கப்பட்டுள்ளன.

குறிப்பு

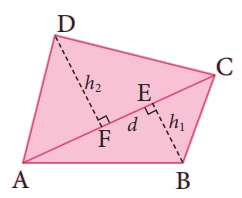
நாற்கரம் ABCD இல் AC என்பது மூலைவிட்டம் (d), BE (h1) மற்றும் DF (h2) ஆகியவை முறையே முனைகள் B மற்றும் D இலிருந்து மூலைவிட்டம் AC இக்கு வரையப்பட்ட செங்குத்துக்கோடுகள் எனில், 

நாற்கரம் ABCD இன் பரப்பளவு = ∆ABC இன் பரப்பளவு + ∆ACD இன் பரப்பளவு 

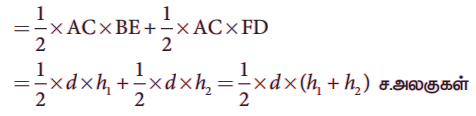
கொடுக்கப்பட்டுள்ள அளவுகளைப் பயன்படுத்திப் பின்வரும் வழிகளில் நாற்கரங்களை வரையும் முறைகளை இப்பகுதியில் காண்போம். 

1. நான்கு பக்கங்கள் மற்றும் ஒரு மூலைவிட்டம் கொடுக்கப்பட்டிருந்தால் 

2. மூன்று பக்கங்கள் மற்றும் இரு மூலைவிட்டங்கள் கொடுக்கப்பட்டிருந்தால் 

3. நான்கு பக்கங்கள் மற்றும் ஒரு கோணம் கொடுக்கப்பட்டிருந்தால் 

4. மூன்று பக்கங்கள் மற்றும் இரண்டு கோணங்கள் கொடுக்கப்பட்டிருந்தால் 

5. இரண்டு பக்கங்கள் மற்றும் மூன்று கோணங்கள் கொடுக்கப்பட்டிருந்தால்

1. நான்கு பக்கங்கள் மற்றும் ஒரு மூலைவிட்டம் கொடுக்கப்பட்டிருக்கும் போது நாற்கரம் வரைதல்

எடுத்துக்காட்டு 5.21

DE = 6 செ.மீ, EA = 5 செ.மீ, AR = 5.5 செ.மீ, RD = 5.2 செ.மீ. மற்றும் DA = 10 செ.மீ. ஆகிய அளவுகளைக் கொண்ட DEAR என்ற நாற்கரம் வரைந்து, அதன் பரப்பளவைக் காண்க. 

தீர்வு:

தரவு : 

DE = 6 செ.மீ, EA = 5 செ.மீ, AR = 5.5 செ.மீ, 

RD = 5.2 செ.மீ மற்றும் ஒரு மூலைவிட்டம் 

DA = 10 செ.மீ 

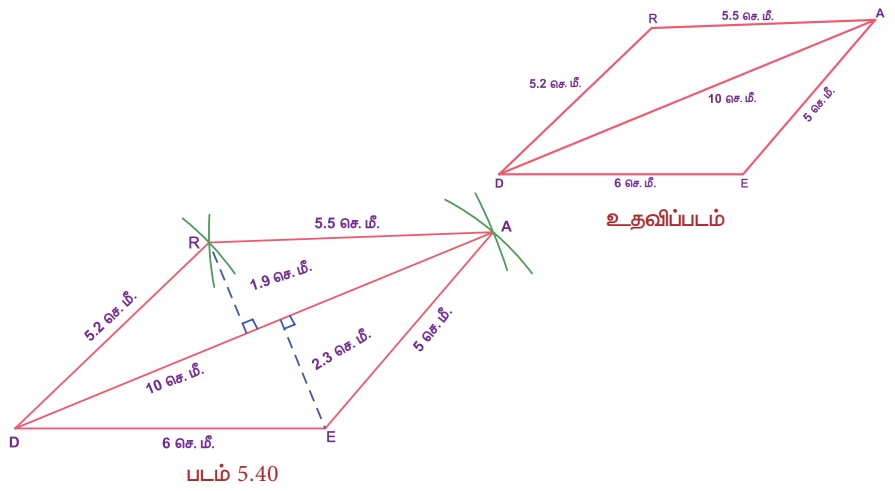
வரைமுறை:

1. DE = 6 செ.மீ. அளவுள்ள ஒரு கோட்டுத்துண்டு வரைக. 

2. D மற்றும் E ஐ மையங்களாகக் கொண்டு, முறையே 10 செ.மீ. மற்றும் 5 செ.மீ. ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை A இல் வெட்டட்டும். DA மற்றும் EA ஐ இணைக்க. 

3. D மற்றும் A ஐ மையங்களாகக் கொண்டு, முறையே 5.2 செ.மீ. மற்றும் 5.5 செ.மீ. ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை R இல் வெட்டட்டும். 

4. DR மற்றும் AR ஐ இணைக்க. 

5. DEAR என்பது தேவையான நாற்கரம் ஆகும்.

பரப்பளவு கணக்கிடுதல் : 

DEAR என்ற நாற்கரத்தின் பரப்பளவு = × d × ( h1 + h2 ) ச.அலகுகள்

=  × 10 × ( 1.9  + 2.3 ) = 5 × 4.2 = 21 செ.மீ2

2. மூன்று பக்கங்கள் மற்றும் இரு மூலைவிட்டங்கள் கொடுக்கப்பட்டிருக்கும் போது நாற்கரம் வரைதல் 

எடுத்துக்காட்டு 5.22

NI = 4.5 செ.மீ, IC = 4.3 செ.மீ, NE = 3.5 செ.மீ, NC = 5.5 செ.மீ. மற்றும் IE = 5 செ.மீ. ஆகிய அளவுகளைக் கொண்ட NICE என்ற நாற்கரம் வரைந்து அதன் பரப்பளவைக் காண்க.

தீர்வு:

தரவு : NI = 4.5 செ.மீ, IC = 4.3 செ.மீ, 

NE = 3.5 செ.மீ. மற்றும் இரண்டு மூலைவிட்டங்கள், 

NC = 5.5 செ.மீ. மற்றும் IE = 5 செ.மீ.

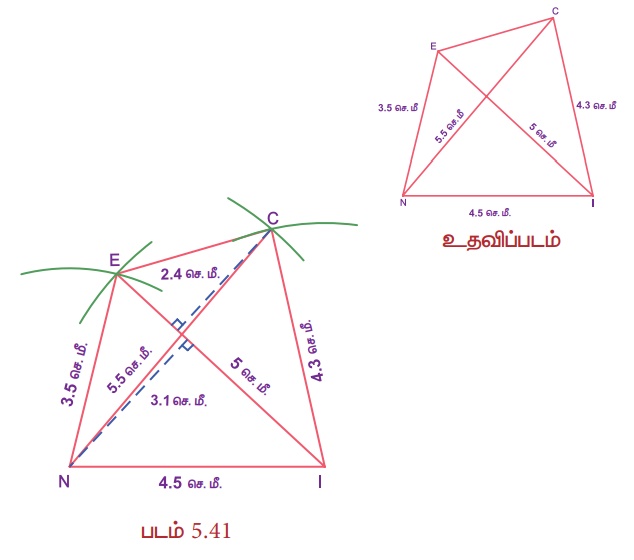
வரைமுறை:

1. NI = 4.5 செ.மீ. அளவுள்ள கோட்டுத்துண்டு வரைக. 

2. N மற்றும் I ஐ மையங்களாகக் கொண்டு, முறையே 5.5 செ.மீ. மற்றும் 4.3 செ.மீ. ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை C இல் வெட்டட்டும்.

3. NC மற்றும் IC ஐ இணைக்க 

4. N மற்றும் I ஐ மையங்களாகக் கொண்டு, முறையே 3.5 செ.மீ. மற்றும் 5 செ.மீ. ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை E இல் வெட்டட்டும்.

5. NE, IE மற்றும் CE ஐ இணைக்க. 

6. NICE என்பது தேவையான நாற்கரம் ஆகும்.

பரப்பளவு கணக்கிடுதல் : 

NICE என்ற நாற்கரத்தின் பரப்பளவு =   × d × ( h1 + h2 ) ச.அலகுகள்

=  × 5 × ( 2.4  + 3.1 ) 

= 2.5 × 5.5 = 13.75 செ.மீ2

3. நான்கு பக்கங்கள் மற்றும் ஒரு கோணம் கொடுக்கப்பட்டிருக்கும் போது நாற்கரம் வரைதல்

எடுத்துக்காட்டு 5.23

MA = 4 செ.மீ, AT = 3.6 செ.மீ, TH = 4.5 செ.மீ, MH = 5 செ.மீ மற்றும் ∠A = 85° ஆகிய அளவுகளைக் கொண்ட MATH என்ற நாற்கரம் வரைந்து, அதன் பரப்பளவைக் காண்க.

தீர்வு:

தரவு: 

MA = 4 செ.மீ, AT = 3.6 செ.மீ, 

TH = 4.5 செ.மீ, MH = 5 செ.மீ. மற்றும் ∠A = 85°.

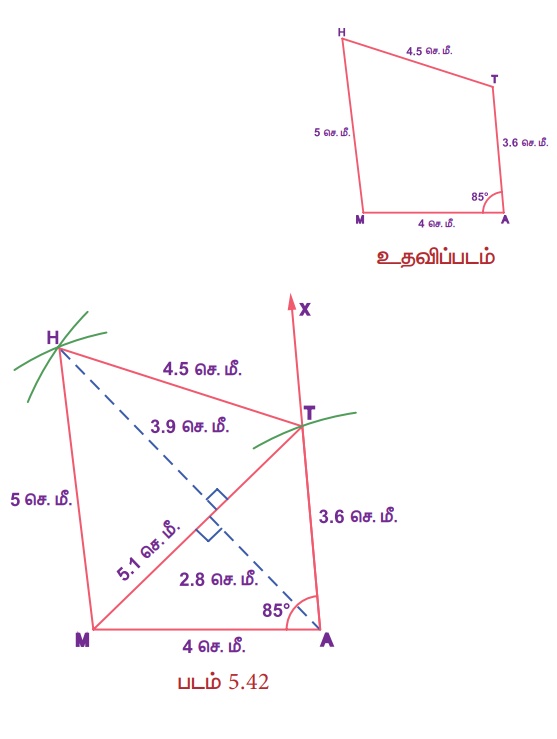
வரைமுறை:

1. MA= 4 செ.மீ. அளவுள்ள கோட்டுத்துண்டு வரைக.

2. ∠A = 85° ஐ வரைக. 

3. A ஐ மையமாகக் கொண்டு, 3.6 செ.மீ. ஆரமுள்ள வில் வரைக. அது கதிர் AX ஐ T இல் வெட்டட்டும்.

4. M மற்றும் T ஐ மையங்களாகக் கொண்டு, முறையே 5 செ.மீ. மற்றும் 4.5 செ.மீ. ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை H இல் வெட்டட்டும்.

5. MH மற்றும் TH ஐ இணைக்க.

6. MATH என்பது தேவையான நாற்கரம் ஆகும்.

பரப்பளவு கணக்கிடுதல் :

MATH என்ற நாற்கரத்தின் பரப்பளவு =  × d × ( h1 + h2 ) ச.அலகுகள்

=  × 5.1 × ( 3.9  + 2.8 ) 

= 2.55 × 6.7 = 17.09 செ.மீ2

4. மூன்று பக்கங்கள் மற்றும் இரண்டு கோணங்கள் கொடுக்கப்பட்டிருக்கும் போது நாற்கரம் வரைதல்

எடுத்துக்காட்டு 5.24

AB = 7 செ.மீ , AD = 5 செ.மீ, CD = 5 செ.மீ, ∠BAC = 50o மற்றும் ∠ABC = 60o ஆகிய அளவுகளைக் கொண்ட ABCD என்ற நாற்கரம் வரைந்து, அதன் பரப்பளவைக் காண்க.

தீர்வு :

தரவு:

AB = 7 செ.மீ, AD = 5 செ.மீ, 

CD = 5 செ.மீ. மற்றும் இரண்டு கோணங்கள் 

∠BAC = 50° மற்றும் ∠ABC = 60°

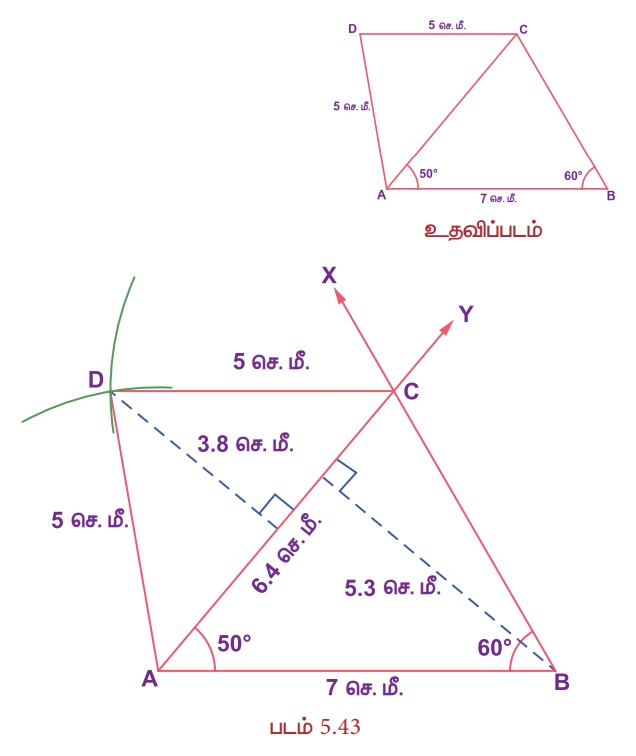
வரைமுறை: 

1. AB = 7 செ.மீ. அளவுள்ள கோட்டுத்துண்டு வரைக. 

2. AB ன் மேல் Aல் ∠BAY = 50° ஐயும் மற்றும் B இல் ∠ABX = 60° ஐயும் உருவாக்குக. அவை C இல் வெட்டட்டும். 

3. A மற்றும் C ஐ மையங்களாகக் கொண்டு, 5 செ.மீ ஆரமுள்ள விற்கள் வரைக. அவை D இல் வெட்டட்டும். 

4. AD மற்றும் CD ஐ இணைக்க. 

5. ABCD என்பது தேவையான நாற்கரம் ஆகும்.

பரப்பளவு கணக்கிடுதல் :

ABCD என்ற நாற்கரத்தின் பரப்பளவு =  (1 / 2) × d × ( h1 + h2 ) ச.அலகுகள்

=  (1/2) × 6.4 × ( 3.8  + 5.3 ) 

= 3.2 × 9.1 = 29.12 செ.மீ2

5. இரண்டு பக்கங்கள் மற்றும் மூன்று கோணங்கள் கொடுக்கப்பட்டிருக்கும் போது நாற்கரம் வரைதல்

எடுத்துக்காட்டு 5.25

PQ = QR = 5 செ.மீ, ∠QPR = 50°, ∠PRS = 40° மற்றும் ∠RPS = 80° ஆகிய அளவுகளைக் கொண்ட PQRS என்ற நாற்கரம் வரைந்து, அதன் பரப்பளவைக் காண்க.

தீர்வு : 

தரவு : 

PQ = 5 செ.மீ, QR = 5 செ.மீ. ∠QPR = 50°, 

∠PRS = 40° மற்றும் ∠RPS = 80°

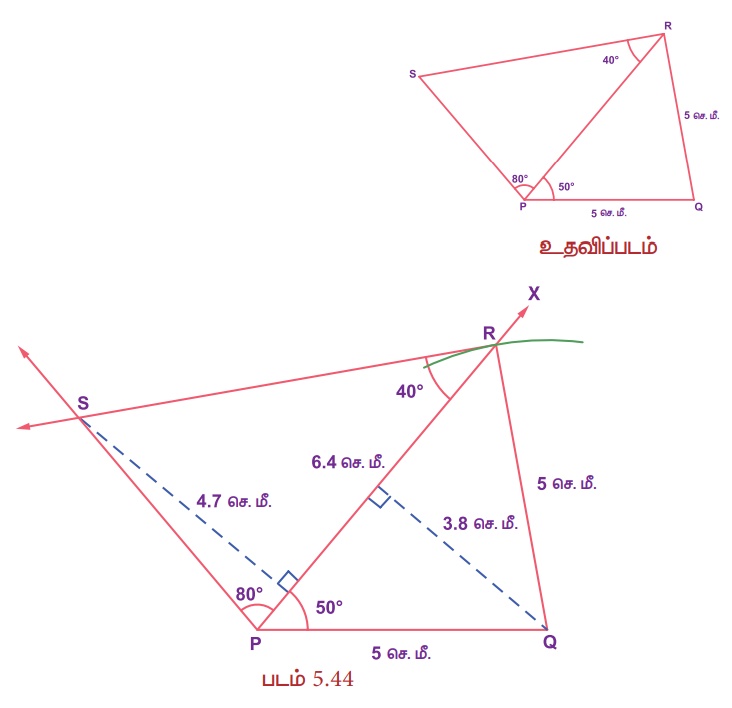
வரைமுறை:

1. PQ = 5 செ.மீ. அளவுள்ள கோட்டுத்துண்டு வரைக. 

2. PQன் மேல் P இல் ∠QPX = 50° ஐ உருவாக்குக. 

3. Q ஐ மையமாகக் கொண்டு, 5 செ.மீ ஆரமுள்ள வில் வரைக. அது PX ஐ R இல் வெட்டட்டும். QR ஐ இணைக்க. 

4. PR ன் மேல் R இல் ∠PRS = 40° ஐயும் மற்றும் P இல் ∠RPS = 80° ஐயும் உருவாக்குக. அவை S இல் வெட்டட்டும். 

5. PQRS என்பது தேவையான நாற்கரம் ஆகும்.

பரப்பளவு கணக்கிடுதல் : 

PQRS என்ற நாற்கரத்தின் பரப்பளவு =  × d × ( h1 + h2 ) ச.அலகுகள்

=  × 6.4 × ( 4.7  + 3.8 ) 

= 3.2 × 8.5 = 27.2 செ.மீ2

சிந்திக்க 

PQ = 5 செ.மீ, QR = 3 செ.மீ, RS = 6 செ.மீ, PS = 7 செ.மீ. மற்றும் PR = 10 செ.மீ. ஆகிய அளவுகளைக் கொண்டு நாற்கரம் அமைக்க இயலுமா? ஏன்?