வடிவொத்த முக்கோணங்கள்

2. வடிவொத்த முக்கோணங்கள்

கொடுக்கப்பட்டுள்ள இரு முக்கோணங்கள் PQR மற்றும் ABC ஆகியவை வடிவொத்தவை (~) ஆகும். ஏனெனில், இரு முக்கோணங்களின் ஒத்த கோணங்கள் சமமாகவும் ஒத்த பக்கங்கள் விகிதசமத்திலும் உள்ளன. அதாவது ∠P = ∠A, ∠Q = ∠B, ∠R = ∠C மற்றும் 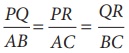ஆகும். இதனை நாம் ∆PQR~∆ABC எனக் குறிக்கலாம். 

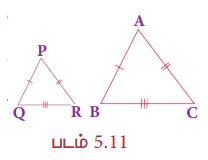
இரண்டு முக்கோணங்கள் வடிவொத்தவை என நிரூபிக்க 4 வழிகள் உண்டு. அவையாவன:

 (i) கோ−கோ−கோ (கோணம்−கோணம்−கோணம்) அல்லது கோ−கோ வடிவொத்தப் பண்பு

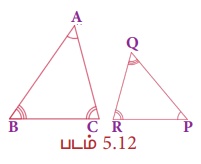
ஒரு முக்கோணத்தின் இரண்டு கோணங்கள், மற்றொரு முக்கோணத்தின் இரண்டு கோணங்களுக்குச் சமம் எனில், அவ்விரு முக்கோணங்களும் வடிவொத்தவை ஆகும். படம் 5.12 இல் ∠A = ∠P, ∠B = ∠Q ஆகும். ஆகவே, ∆ABC ~ ∆PQR.

 (ii) ப−கோ−ப (பக்கம்−கோணம்−பக்கம்) வடிவொத்தப் பண்பு

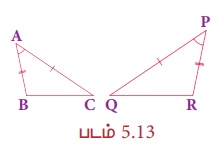
ஒரு முக்கோணத்தின் இரண்டு பக்கங்கள் மற்றொரு முக்கோணத்தின் இரண்டு பக்கங்களுக்கு விகிதசமத்திலும் அவ்விரண்டு பக்கங்கள் உள்ளடக்கிய கோணங்கள் சமமாகவும் இருந்தால், அவ்விரு  முக்கோணங்கள் வடிவொத்தவை ஆகும். படம் 5.13 இல் 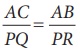 மற்றும் ∠A = ∠P. ஆகவே, ∆ACB ~ ∆PQR.

(iii) ப−ப−ப (பக்கம்−பக்கம்−பக்கம்) வடிவொத்தப் பண்பு 

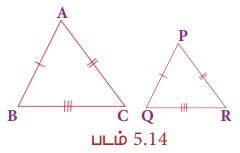
இரண்டு முக்கோணங்களின் ஒத்த பக்கங்கள் சமவிகிதத்தில் அமையும் எனில், அவை வடிவொத்தவை ஆகும். அதாவது, 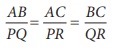எனில், ∆ABC ~ ∆PQR ஆகும்.

(iv) செ−க−ப (செங்கோணம்−கர்ணம்−பக்கம்) வடிவொத்தப் பண்பு

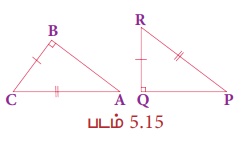
ஒரு செங்கோண முக்கோணத்தின் கர்ணம் மற்றும் ஒரு பக்கம், மற்றொரு செங்கோண முக்கோணத்தின் கர்ணம் மற்றும் ஒரு பக்கத்திற்குச் சமவிகிதத்தில் அமையும் எனில், அவை வடிவொத்தவை ஆகும். அதாவது, ∠B= ∠Q=90°  மற்றும் 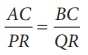எனில், ∆ABC ~ ∆PQR.

உங்களுக்குத் தெரியுமா?

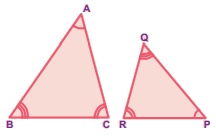
∆ABC ~ ∆PQR எனில் ∆ABC − இன் பக்கங்கள் AB, BC மற்றும் AC ஆகியவை, ∆PQR−இன் பக்கங்களான PQ, QR மற்றும் PR ஆகியவற்றிற்கு ஒத்த பக்கங்கள் ஆகும். மேலும் கோணங்கள் A, B மற்றும் C இக்கு ஒத்தக் கோணங்கள் முறையே P,Q மற்றும் R ஆகும். வடிவொத்த முக்கோணங்களுக்கு வரிசை மாறாமல் பெயரிடுதல் முக்கியமாகும். எடுத்துக்காட்டாக, ∆ABC ~ ∆PQR எனில், ∆BAC ஆனது ∆PQR இக்கு வடிவொத்தவையாக இருக்காது.

எடுத்துக்காட்டு 5.5

படம் 5.16 இல், ∆PQR~∆XYZ, எனில் a மற்றும் b ஐக் காண்க.

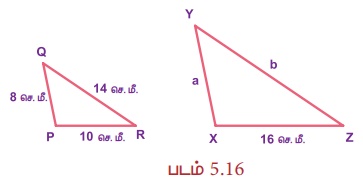
தீர்வு: 

இங்கு, ∆PQR ~ ∆XYZ

∴ அவற்றின் ஒத்த பக்கங்கள் விகிதசமத்தில் இருக்கும். 

= 22.4 செ.மீ.

குறிப்பு 

• அனைத்து வட்டங்களும், சதுரங்களும்  எப்போதும் வடிவொத்தவையாக இருக்கும். 

• அனைத்துச் செவ்வகங்களும் எப்போதும் வடிவொத்தவையாக இருக்க வேண்டியதில்லை. 

• இரு கோணங்கள் சர்வசமமாகவும், மிகை  நிரப்பிகளாகவும் இருக்குமாயின், அவை செங்கோணங்கள் ஆகும். 

• அனைத்து சர்வசம முக்கோணங்களும் வடிவொத்த முக்கோணங்கள் ஆகும்.

எடுத்துக்காட்டு 5.6

 (கோ−கோ வடிவொத்தப் பண்பை விளக்குகிறது ) படம் 5.17 இல், ∠ABC ≡ ∠EDC மற்றும் ∆CDE இன் சுற்றளவு 27 அலகுகள் எனில் AB ≡ EC என நிறுவுக.

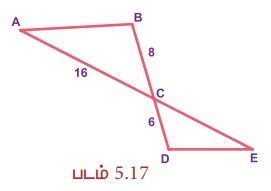
நிரூபணம்:

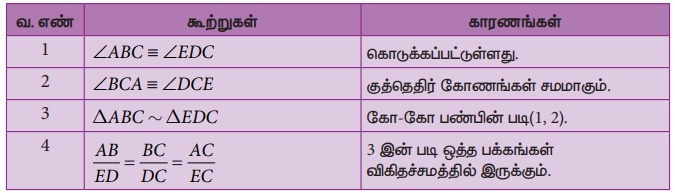
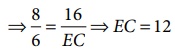⇒12 அலகுகள்

∆CDE இன் சுற்றளவு 27 அலகுகள் எனக் கொடுக்கப்பட்டுள்ளது.

∴ ED + DC + EC = 27 ⇒ ED + 6 + 12 = 27 ⇒ ED = 27−18 = 9 அலகுகள் 

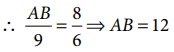 அலகுகள். ஆகவே AB = EC.

எடுத்துக்காட்டு 5.7 

(கோ − கோ வடிவொத்தப் பண்பை விளக்குகிறது)

கொடுக்கப்பட்டுள்ள படம் 5.18 இல் ∠1 ≡ ∠3 மற்றும் ∠2 ≡ ∠4 எனில், ∆BIG ~ ∆FAT என நிறுவுக. மேலும் FA ஐக் காண்க.

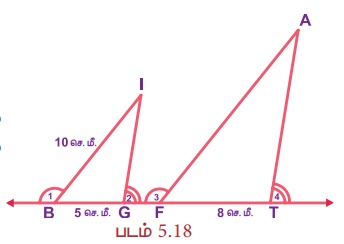
நிரூபணம்:

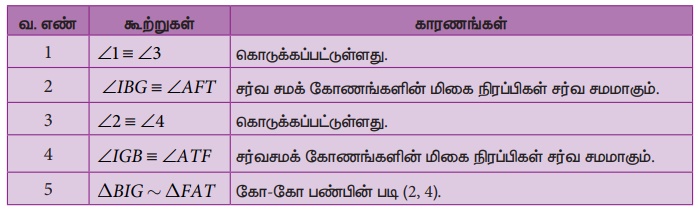
மேலும், அவற்றின் ஒத்த பக்கங்கள் விகிதச்சமத்தில் இருக்கும்.

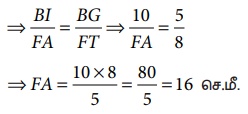
 = 16 செ.மீ.  

எடுத்துக்காட்டு 5.8 

(ப−கோ−ப வடிவொத்தப் பண்பை விளக்குகிறது)

கொடுக்கப்பட்டுள்ள படம் 5.19 இல் RU இன் மையப்புள்ளி A மற்றும் RN இன் மையப்புள்ளி T எனில் ∆RAT  ~  ∆RUN என நிறுவுக

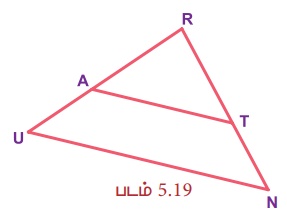
நிரூபணம்:

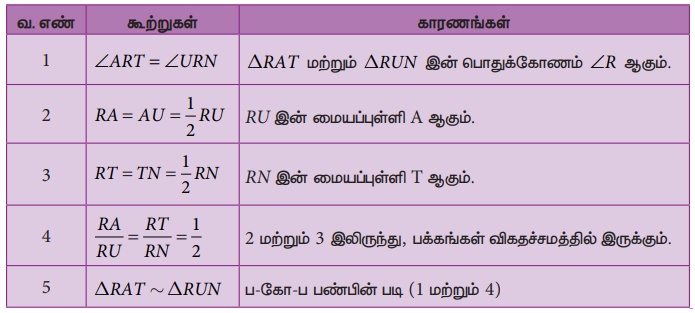
எடுத்துக்காட்டு 5.9 

(ப−ப−ப வடிவொத்தப் பண்பை விளக்குகிறது)

படம் 5.20 இல்  ∆PQR~ ∆PRS என நிறுவுக. 

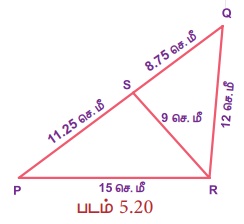
தீர்வு :

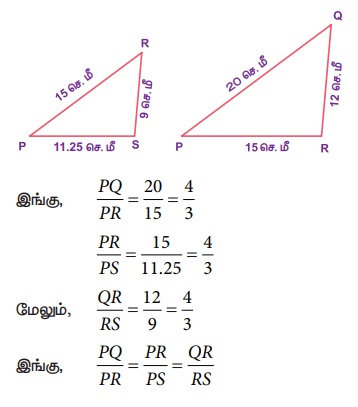
ஆக இருப்பதைக் காணலாம். 

அதாவது, அவற்றின் ஒத்த பக்கங்கள் விகிதசமத்தில் இருக்கின்றன.

∴ ப−ப−ப பண்பின் படி,                 ∆PQR ~∆PRS .

எடுத்துக்காட்டு 5.10 

(செ−க−ப வடிவொத்தப் பண்பை விளக்குகிறது)

ஒரு மனிதனின் உயரத்தாலும் நிழலாலும் அமையும் முக்கோணமானது, அருகிலுள்ள மரத்தின் உயரத்தாலும் அதன் நிழலாலும் அமையும் முக்கோணத்திற்கு வடிவொத்தவையாக உள்ளது எனில், மரத்தின் உயரம் என்ன?

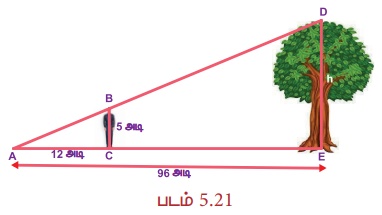
தீர்வு:

இங்கு, ∆ABC~∆ADE (கொடுக்கப்பட்டுள்ளது )

∴ அவற்றின் ஒத்த பக்கங்கள் விகிதசமத்தில் இருக்கும். (செ− க − ப பண்பின் படி).

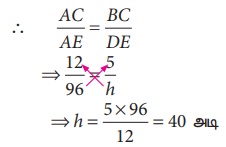
⇒ h = 5 × 96 = 40 அடி

∴ மரத்தின் உயரம் 40 அடியாகும்.

செயல்பாடு

ஆசிரியர் ஓர் அட்டை அல்லது படத்தாளிலிருந்து, பல்வேறு வடிவொத்த மற்றும் சர்வசம முக்கோணங்களை வெட்டியெடுத்து, மாணவர்களிடம், முக்கோணங்களின் மீதுள்ள அளவுகளைக் கொண்டு, எந்தச் சோடி முக்கோணங்கள் வடிவொத்தவை மற்றும் சர்வசமமானவை என்பதைக் காணச் செய்தல் வேண்டும்.