கேள்வி பதில்கள், தீர்வுகள் | 8 ஆம் வகுப்பு கணக்கு : அலகு 5 : வடிவியல் - சிந்திக்க, இவற்றை முயல்க, நினைவு கூர்தல், செயல்பாடு | 8th Maths : Chapter 5 : Geometry
8 ஆம் வகுப்பு கணக்கு : அலகு 5 : வடிவியல்
சிந்திக்க, இவற்றை முயல்க, நினைவு கூர்தல், செயல்பாடு
இவற்றை முயல்க
வடிவொத்த மற்றும் சர்வசம உருவங்களின் சோடிகளை அடையாளம் கண்டு, அவற்றின் எழுத்துச் சோடிகளை எழுதுக.
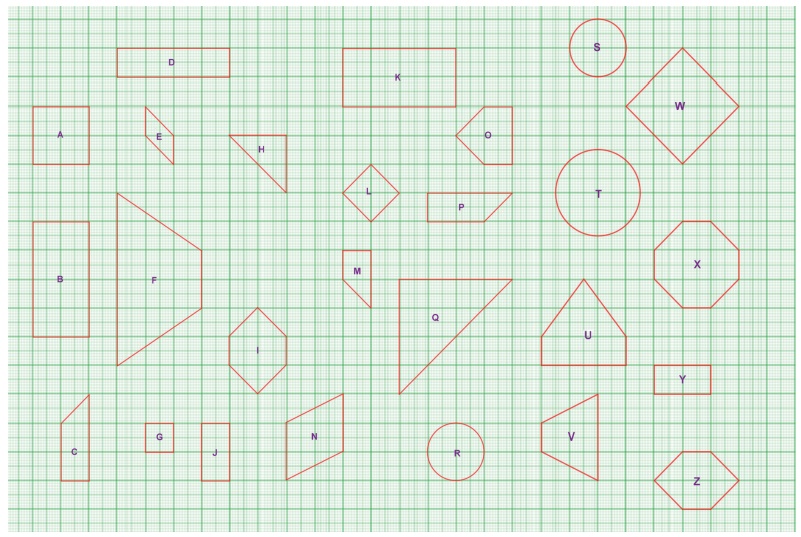
இவற்றை முயல்க
பின்வருவனவற்றை அவற்றின் சர்வசமப் பண்புகளைக் கொண்டு பொருத்துக.
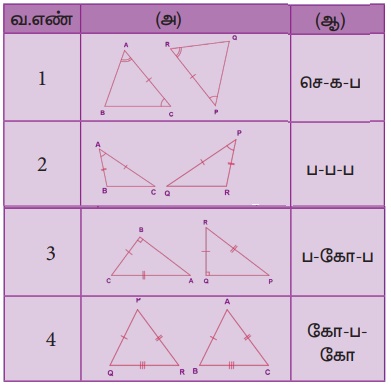
சிந்திக்க
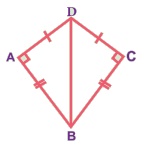
படத்தில் DA = DC மற்றும் BA = BC. முக்கோணங்கள் DBA மற்றும் DBC ஆகியவை சர்வ சமமா? ஏன்?
செயல்பாடு
ஆசிரியர் ஓர் அட்டை அல்லது படத்தாளிலிருந்து, பல்வேறு வடிவொத்த மற்றும் சர்வசம முக்கோணங்களை வெட்டியெடுத்து, மாணவர்களிடம், முக்கோணங்களின் மீதுள்ள அளவுகளைக் கொண்டு, எந்தச் சோடி முக்கோணங்கள் வடிவொத்தவை மற்றும் சர்வசமமானவை என்பதைக் காணச் செய்தல் வேண்டும்.
செயல்பாடு
1. பிதாகரஸ் மூன்றன் தொகுதியைப் பின்வருமாறு நாம் உருவாக்கலாம்.
m மற்றும் n ஆகியவை ஏதேனும் இரண்டு மிகை முழுக்கள் என்க (m > n).
a = m2 − n2 , b = 2mn மற்றும் c = m2 + n2 எனில், (a, b, c) ஆனது ஒரு பிதாகரஸ் மூன்றன் தொகுதியாகும். (ஏன்? எனச் சிந்திக்க)
அட்டவணையை நிரப்புக.

2. கர்ணம் 85 ஆகவும் மற்ற இரு பக்க அளவுகள் முழுக்களாகவும் உடைய செங்கோண முக்கோணத்தின் பக்க அளவுகளைக் காண்க.
செயல்பாடு
1. முக்கோண வடிவ காகிதத்தை எடுத்துக் கொள்க (குறுங்கோண முக்கோணத்தைக் கொண்டு தொடங்குவோம்). அதற்கு ABC எனப் பெயரிடுக.
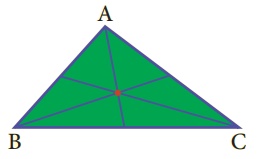
2. மடிப்புக் கோடானது உச்சிப்புள்ளி A வழியாகவும், B ஆனது C இன் மேல் பொருந்தும் நிலையில் BC ஐ சந்திக்குமாறும் காகிதத்தினை மடிக்க
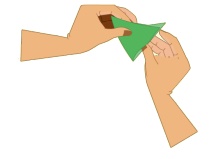
3. BC இன் மையப்புள்ளி M ஐக் குறிக்க.
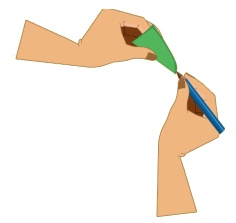
4. தெளிவாகக் காண விரும்பினால், இப்போது நீங்கள் நடுக்கோடு AM ஐ வரைந்து கொள்ளலாம் (அல்லது மடிப்பாகவே இருக்கலாம்)
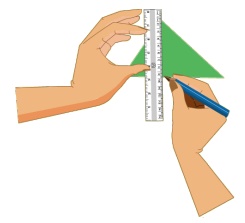
5. இதேபோன்று மடித்து, மற்ற இரண்டு நடுக்கோடுகளையும் வரைக.
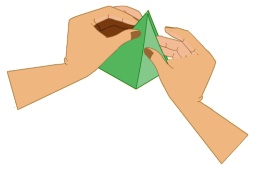
6. அனைத்து நடுக்கோடுகளும் ஒரேபுள்ளி வழிச் செல்கின்றனவா?
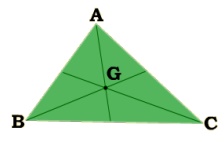
இப்போது இதே செயல்பாட்டினை மீண்டும் விரிகோண மற்றும் செங்கோண முக்கோணங்களுக்கும் செய்க. உங்களின் முடிவு என்ன?
எந்தவொரு முக்கோணத்தின் மூன்று நடுக்கோடுகளும் ஒருபுள்ளி வழிச் செல்லும் கோடுகள் ஆகும்.
செயல்பாடு
1. ஒரு குறுங்கோண முக்கோண வடிவில் வெட்டப்பட்டுள்ள காகிதத்தை எடுத்துக் கொள்க, அதற்கு ABC எனப் பெயரிடுக.

2. முக்கோணத்தின் ஒரு பக்கமானது அதன் மீது பொருந்துமாறும் அப்பக்கத்திற்கு எதிரேயுள்ள உச்சியைப் பெற்றிருக்குமாறும் அம்முக்கோணத்தை மடிக்க.
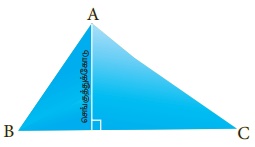
3. நீங்கள் செங்குத்துக்கோட்டை தெளிவாகக் காண விரும்பினால் இப்போது நீங்கள் செங்குத்துக்கோடு AM ஐ வரைந்து கொள்ளலாம்.
இதேபோன்று மற்ற இரு பக்கங்களின் செங்குத்துக்கோடுகளையும் காண்க. மேலும், உங்கள் ஆசிரியரின் உதவியுடன் செங்கோண மற்றும் விரிகோண முக்கோணங்களின் செங்குத்துக்கோடுகளையும் காண்க. ஒரு முக்கோணத்தின் அனைத்துச் செங்குத்துக்கோடுகளும் ஒரு புள்ளி வழியாகச் செல்கின்றனவா?
எந்தவொரு முக்கோணத்தின் மூன்று செங்குத்துக்கோடுகளும் ஒருபுள்ளி வழிச் செல்லும் கோடுகள் ஆகும்.
அவ்வாறு சந்திக்கும் புள்ளியானது அதன் செங்கோட்டுமையம் ஆகும். இது H என்ற எழுத்தால் குறிக்கப்படுகிறது.
சிந்திக்க
1. குறுங்கோண முக்கோணத்தில், மூன்று செங்குத்துக் கோடுகளும் முக்கோணத்தின் உள்பகுதியிலேயே அமையும்.
அதன் செங்கோட்டு மையம் எங்கு அமையும்?
முக்கோணத்தின் உள்பகுதியில் அமையுமா?
அல்லது வெளிப்பகுதியில் அமையுமா?
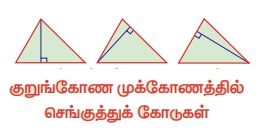
2. செங்கோண முக்கோணத்தில், கர்ணத்திற்குச் செங்குத்தாக உள்ள செங்குத்துக்கோடானது உள்பகுதியிலும், மற்ற இரண்டு செங்குத்துக்கோடுகள் செங்கோணத்தைத் தாங்கும் பக்கங்களாகவும் அமையும். இவ்வகை முக்கோணங்களுக்குச் செங்கோட்டுமையம் எங்கு அமையும் எனக் கூற இயலுமா?
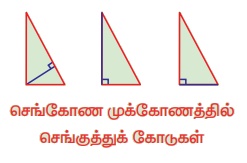
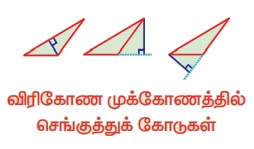
3. விரிகோண முக்கோணத்தில், விரிகோணத்தைத் தாங்கும் உச்சியிலிருந்து வரையப்படும் செங்குத்துக்கோடு முக்கோணத்தின் உள்பகுதியிலும் குறுங்கோணங்களைத் தாங்கும் உச்சிகளிலிருந்து வரையப்படும் மற்ற இரு செங்குத்துக்கோடுகள் முக்கோணத்தின் வெளிப்பகுதியிலும் அமையும். இவ்வகை முக்கோணங்களுக்குச் செங்கோட்டு மையம் எங்கு அமையும் எனக் கூற இயலுமா?
செயல்பாடு
காகித மடிப்பு முறையில் முக்கோணத்தின் பக்கங்களின் மையக்குத்துக் கோடுகள் ஒரே புள்ளி வழிச் செல்வதை நாம் காண இயலும். முயற்சி செய்க!
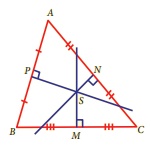
எந்தவொரு முக்கோணத்தின் பக்கங்களின் மையக்குத்துக்கோடுகளும் ஒருபுள்ளி வழிச் செல்லும் கோடுகளாகும்.
நடுக்கோட்டு மையம் காண்பதற்குச் செய்ததைப் போன்றே, குறுங்கோண, '' விரிகோண, செங்கோண, இருசமபக்க மற்றும் சமபக்க முக்கோணம் போன்ற வெவ்வேறு வகை முக்கோணங்களுக்கும் இச்செயல்பாட்டினை மீண்டும் செய்க. இவ்வகையில் சமபக்க முக்கோணங்களின் மையக்குத்துக் கோடுகள் ஏதேனும் சிறப்புத் தன்மையைப் பெற்றுள்ளனவா?
செயல்பாடு
காகித மடிப்பு முறையில் பின்வருவனவற்றைச் சரியானவையா என ஆராய்க :
1. குறுங்கோண முக்கோணத்தின் சுற்றுவட்டமையமானது அம்முக்கோணத்தின் உள்பகுதியிலேயே அமையும்.
2. விரிகோண முக்கோணத்தின் சுற்றுவட்டமையானது அம்முக்கோணத்தின் வெளிப்பகுதியிலேயே அமையும்.
3. செங்கோண முக்கோணத்தின் சுற்றுவட்டமையானது அம்முக்கோணத்தின் கர்ணத்தின் மையப்புள்ளியில் அமையும்.
செயல்பாடு
1. முக்கோண வடிவில் வெட்டப்பட்டுள்ளக் காகிதத்தினை எடுத்துக்கொள்க.
அதற்கு ABC எனப் பெயரிடுக.
2. எதிர்ப்பக்கங்கள் ஒன்றன்மீது ஒன்று பொருந்துமாறும், உச்சிப்புள்ளியைப் பெற்றிருக்குமாறும் முக்கோணத்தினை மடிக்க. இதேபோன்று மீண்டும் செய்து மற்ற இரண்டு கோணங்களின் கோண இருசமவெட்டிகளைக் காண்க.
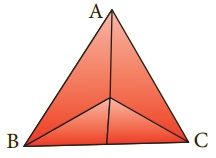
3. அனைத்து மடிப்புக் கோடுகளையும் வரைக.
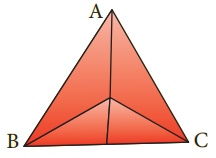
அனைத்துக் கோண இருசம வெட்டிகளும் ஒரே புள்ளி வழிச் செல்கின்றனவா?
இதே செயல்பாட்டினை மீண்டும் விரிகோண மற்றும் செங்கோண முக்கோணங்களுக்கும் செய்து பார்க்கவும். உங்களின் முடிவு என்ன? அனைத்து வகை முக்கோணங்களிலும், கோண இருசமவெட்டிகள் ஒரே புள்ளி வழிச் செல்கின்றனவா? ஆம்,
எந்தவொரு முக்கோணத்தின் மூன்று கோண இருசமவெட்டிகளும் ஒரு புள்ளி வழிச் செல்லும் கோடுகள் ஆகும்.
இவற்றை முயல்க
ஒவ்வொரு முக்கோணத்திலும் கொடுக்கப்பட்டுள்ள கோடுகளின் வகைகளை அடையாளம் காண்க.
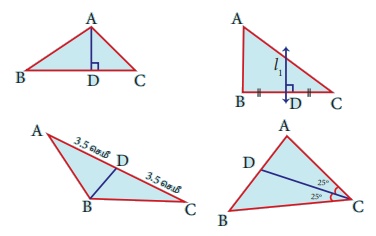
(நடுக்கோடு, செங்குத்துக்கோடு, மையக்குத்துக்கோடு, கோண இருசமவெட்டி)
(i) AD = …………….
(ii) l1 = ……………..
(iii) BD = ……………
(iv) CD = …………….
செயல்பாடு
1. காகித மடிப்பு முறையில் சமபக்க முக்கோணத்தின் நடுக்கோட்டுமையம், செங்கோட்டு மையம், சுற்றுவட்டமையம் மற்றும் உள்வட்டமையம் ஆகியவற்றைக் காண்க . அவை ஒரே புள்ளியில் அமைகிறதா ?
2. காகித மடிப்பு முறையில் ஒரு முக்கோணத்தின் நடுக்கோட்டுமையம் (G), செங்கோட்டுமையம் (H), சுற்றுவட்டமையம் (S) மற்றும் உள்வட்டமையம் (I) ஆகியவற்றைக் காண்க. G, H, S மற்றும் I ஐ இணைக்க. அவை ஒரு கோடமைப் புள்ளிகளா?
சிந்திக்க
PQ = 5 செ.மீ, QR = 3 செ.மீ, RS = 6 செ.மீ, PS = 7 செ.மீ. மற்றும் PR = 10 செ.மீ. ஆகிய அளவுகளைக் கொண்டு நாற்கரம் அமைக்க இயலுமா? ஏன்?
இவற்றை முயல்க
1. சரிவகத்தின் பரப்பளவு __________ ஆகும்.
2. சரிவகத்தின் இணைப்பக்கங்களுக்கு இடைப்பட்ட தொலைவு __________….. எனப்படுகிறது.
3. ஒரு சரிவகத்தின் உயரமும் இணைப்பக்கங்களும் முறையே 5 செ.மீ, 7 செ.மீ மற்றும் 5 செ.மீ எனில், அதன் பரப்பளவு __________….. ஆகும்.
4. இருசமபக்கச் சரிவகத்தில், இணையற்ற பக்கங்கள் __________.. ஆக இருக்கும்.
5. சரிவகம் வரைய __________.. அளவுகள் போதுமானது.
6. சரிவகத்தின் பரப்பளவும் இணைப்பக்கங்களின் கூடுதலும் 60 செ.மீ2 மற்றும் 12 செ.மீ எனில், அதன் உயரம் __________…. ஆகும்.
கீழே கொடுக்கப்பட்டுள்ள அளவுகளைப் பயன்படுத்தி சரிவகம் வரையும் முறைகளைக் காண்போம்.
1. மூன்று பக்கங்கள் மற்றும் ஒரு மூலைவிட்டம்.
2. மூன்று பக்கங்கள் மற்றும் ஒரு கோணம்.
3. இரு பக்கங்கள் மற்றும் இரு கோணங்கள்.
4. நான்கு பக்கங்கள்.
செயல்பாடு
1. ஒரு சோடி சமமற்ற நீளமுள்ள குச்சிகளை (தென்னங்குச்சியின் துண்டுகள் என்க) அவற்றின் ஒரு முனையில் இணைத்தவாறு வைக்கவும்.

2. இப்போது, அதபோன்று மற்றொரு சோடியைச் செய்து முதலில் வைத்துள்ள தென்னங்குச்சிகளின் இணைக்கப்படாத முனைகளுடன் சந்திக்குமாறு வைக்கவும்.

கிடைக்கப்பெறும் மூடிய வடிவத்தின் பெயர் என்ன? அது ஒரு நாற்கரமாகும். அதற்கு ABCD எனப் பெயரிடுக . அதில் எத்தனை பக்கங்கள் உள்ளன? அதன் மூலைவிட்டங்கள் என்னென்ன? மூலைவிட்டங்கள் சமமாக உள்ளனவா? அதன் கோணங்கள் சமமாக உள்ளனவா?
மேற்கூறிய செயல்பாட்டில், பின்வருமாறு உள்ள நாற்கரங்களைப் பெற இயலுமா?
(i) அனைத்துக் கோணங்களும் குறுங்கோணங்கள்.
(ii) அனைத்துக் கோணங்களும் விரிகோணங்கள்.
(iii) இரண்டு கோணங்கள் விரிகோணங்கள்.
(iv) ஏதேனும் ஒரு கோணம் செங்கோணம்.
(v) ஏதேனும் இரு கோணங்கள் செங்கோணங்கள்.
(vi) மூலைவிட்டங்கள் ஒன்றுக்கொன்று செங்குத்து.
செயல்பாடு
1. ஒரு சோடி 30°−60°−90° மூலைமட்டங்களைப் படத்தில் காட்டியுள்ளவாறு வைக்கவும்.
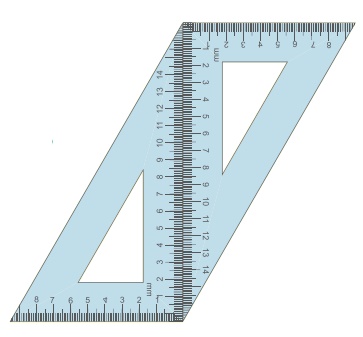
(i) என்ன வடிவத்தை நாம் பெறுகிறோம்? அது ஓர் இணைகரம் ஆகும்.
(ii) அதன் எதிர்ப்பக்கங்கள் இணையாக உள்ளதா?
(iii) அதன் எதிர்ப்பக்கங்கள் சமமாக உள்ளனவா?
(iv) அதன் மூலைவிட்டங்கள் சமமாக உள்ளனவா?
(v) மற்றொரு சோடி மூலைமட்டங்களைப் பயன்படுத்தியும் இதே வடிவத்தைப் பெற இயலுமா?
2. இச்செயல்பாட்டிற்கும், ஒரு சோடி 30°−60°−90° மூலைமட்டங்கள் நமக்குத் தேவை. அவற்றைப் படத்தில் காட்டியுள்ளவாறு வைக்க.
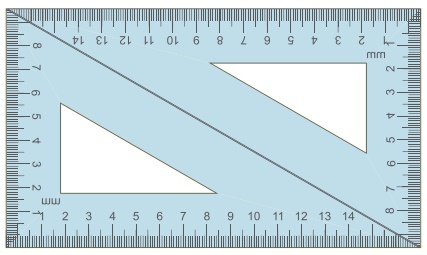
(i) என்ன வடிவத்தை நாம் பெறுகிறோம்?
(ii) அது ஓர் இணைகரமா? அது ஒரு நாற்கரம் ஆகும். உண்மையில் அது ஒரு செவ்வகம் ஆகும். (எப்படி?)
(iii) அவற்றின் பக்கங்களின் நீளம், கோணங்கள் மற்றும் மூலைவிட்டங்களைப் பற்றி என்ன கூற இயலும்.
அவற்றை விவாதித்துப் பட்டியலிடுக.
3. மேற்கண்ட செயல்பாட்டினை, ஒரு சோடி 45°−45°−90° மூலைமட்டங்களைப் பயன்படுத்தி மீண்டும் செய்க.
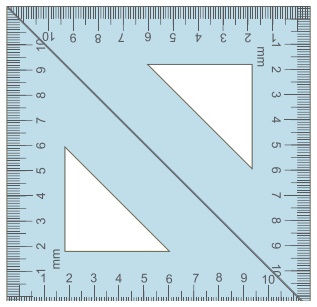
(i) இப்போது என்ன வடிவமாக மாறுகிறது? அது ஓர் இணைகரமா? அது ஒரு சதுரமாக மாறியுள்ளது. (எப்படி நிகழ்ந்தது?)
(ii) அதன் பக்கங்களின் நீளங்கள், கோணங்கள் மற்றும் மூலைவிட்டங்களைப் பற்றி என்ன கூற இயலும்?
அவற்றை விவாதித்துப் பட்டியலிடுக.
(iii) செவ்வகத்தைப் பற்றி நாம் தொகுத்த பட்டியலிலிருந்து இது எவ்வாறு வேறுபடுகிறது?
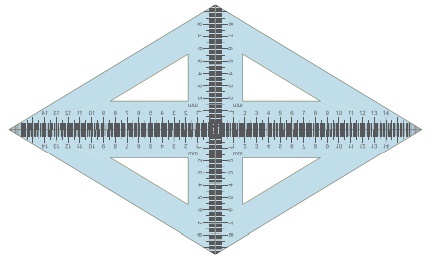
4. 30°−60°−90° கோண அளவுள்ள நான்கு ஒத்த கோணமானிகளையே மீண்டும் இச்செயல்பாட்டிற்குப் பயன்படுத்துவோம். அவை எவ்வாறு ஒன்றையொன்று தொட்டுக்கொள்ளுமாறு வைக்கப்பட்டுள்ளன எனக் கவனமாகக் குறித்துக் கொள்க.
(i) இப்போது, நமக்கு இணைகரம் கிடைக்கிறதா?
(ii) அவற்றின் பக்கங்கள், கோணங்கள் மற்றும் மூலைவிட்டங்கள் ஆகியவற்றைப் பற்றி நாம் என்ன கூற இயலும்?
(iii) அவற்றின் மூலைவிட்டங்களின் சிறப்பு என்ன?
மேற்கண்ட செயல்பாடுகளிலிருந்து கிடைக்கப்பெற்ற விளைவுகளின் அடிப்படையில், இணைகரங்களாக அமையும் சில சிறப்பு நாற்கரங்களின் பல்வேறு பண்புகளையும் நாம் அட்டவணைப்படுத்துவோம்.
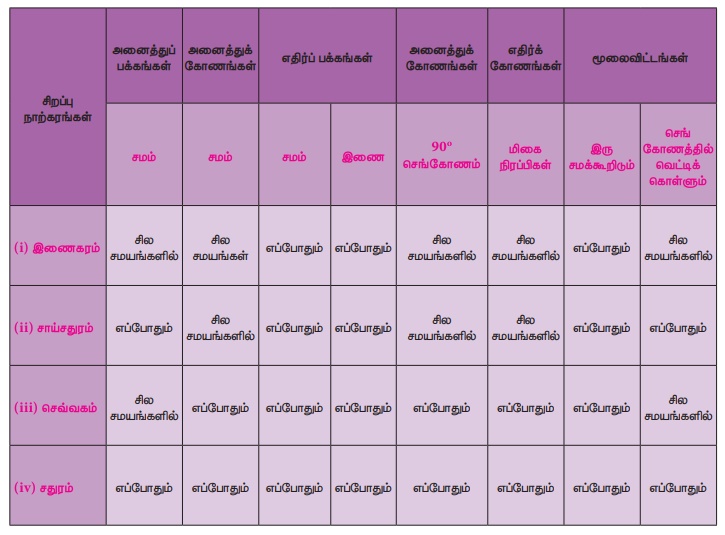
இவற்றை முயல்க
1. சரியா தவறா எனக் கூறுக:
(அ) சதுரமானது ஒரு சிறப்புச் செவ்வகம் ஆகும்.
(ஆ) சதுரமானது ஓர் இணைகரம் ஆகும்.
(இ) சதுரமானது ஒரு சிறப்புச் சாய்சதுரம் ஆகும்.
(ஈ) செவ்வகமானது ஓர் இணைகரம் ஆகும்.
2. பின்வரும் நாற்கரங்களின் பெயர்களை எழுதுக.
(அ) மூலைவிட்டங்கள் ஒன்றுக்கொன்று இருசமக் கூறிடும்.
(ஆ) மூலைவிட்டங்கள் ஒன்றுக்கொன்று செங்குத்தாக இருசமக்கூறிடும்.
(இ) வெவ்வேறு நீளமுள்ள மூலைவிட்டங்களைப் பெற்றிருக்கும்.
(ஈ) சமநீளமுள்ள மூலைவிட்டங்களைப் பெற்றிருக்கும்.
(உ) எதிர்ப்பக்கங்கள் இணையாக இருக்கும்.
(ஊ) எதிர்க்கோணங்கள் சமமாக இருக்கும்.
3. படத்தில் காட்டியுள்ளவாறு, ஒரு கோடிட்ட தாளில் இரண்டு குச்சிகள் வைக்கப்பட்டுள்ளன. நான்கு முனைகளையும் இணைப்பதால் கிடைக்கும் வடிவத்தின் பெயர் என்ன?
(அ) 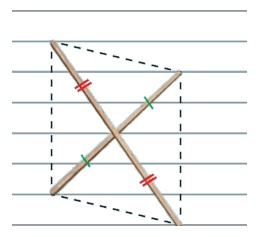
இரு வெவ்வேறு நீளமுள்ள குச்சிகள் மையப்புள்ளியில் சந்திக்குமாறு வைக்கப்பட்டுள்ளன.
(ஆ) 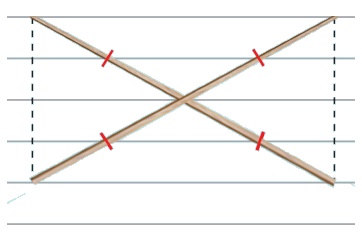
இரு சமநீளமுள்ள குச்சிகள் மையப்புள்ளியில் சந்திக்குமாறு வைக்கப்பட்டுள்ளன.
(இ) 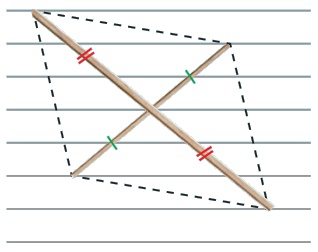
இரு வெவ்வேறு நீளமுள்ள குச்சிகள் செங்குத்தாக இரு சமக்கூறிடுமாறு வைக்கப்பட்டுள்ளன.
(ஈ) 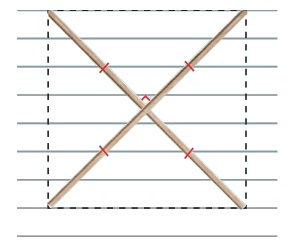
இரு சம அளவு நீளமுள்ள குச்சிகள் மையப்புள்ளியில் செங்குத்தாக வெட்டிக் கொள்ளுமாறு வைக்கப்பட்டுள்ளன.
(உ) 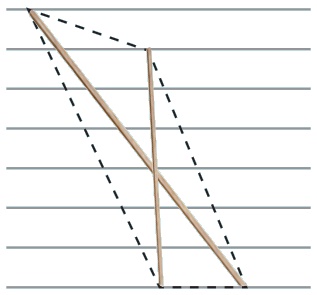
இரு வெவ்வேறு நீளமுள்ள குச்சிகள், கீழ் முனைகள் ஒரே கோட்டிலும் மேல் முனைகள் ஒரே கோட்டில் அமையாதவாறும் மையப்புள்ளியில் வெட்டிக் கொள்ளாதவாறும் வைக்கப்பட்டுள்ளன.
(ஊ) 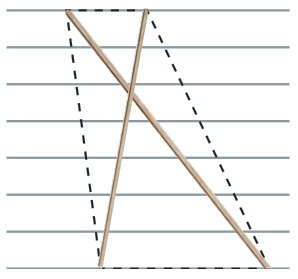
இரு வெவ்வேறு நீளமுள்ள குச்சிகள், கீழ் முனைகளும் மேல் முனைகளும் ஒரே கோட்டில் அமையுமாறும் மையப்புள்ளியில் வெட்டிக் கொள்ளாதவாறும் வைக்கப்பட்டுள்ளன.