முக்கோணத்தின் மையக்குத்துக்கோடுகள்

முக்கோணத்தின் மையக்குத்துக்கோடுகள்

பின்வரும் கருத்துக்களை நாம் முதலில் நினைவு கூர்வோம். 

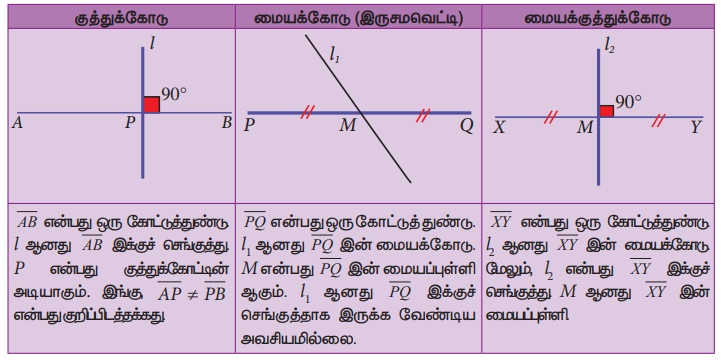
முக்கோணம் ABC ஐக் கருத்தில் கொள்க. அதற்கு மூன்று பக்கங்கள் உள்ளன. ஒவ்வொரு பக்கத்திற்கும் ஒரு மையக்குத்துக்கோட்டினைப் பின்வருமாறு நீங்கள் பெற இயலும்.

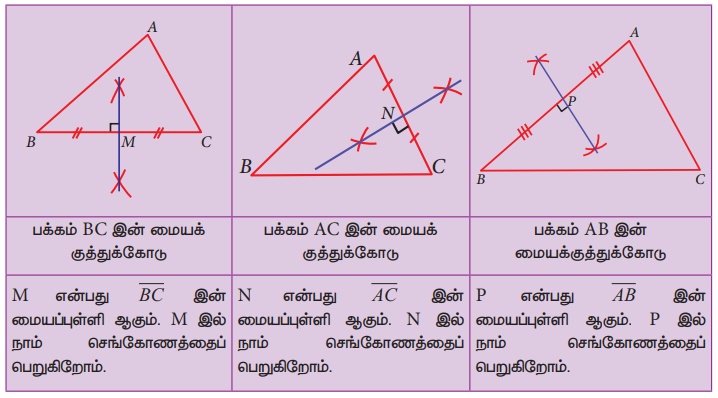
ஒரு முக்கோணத்தின் மூன்று மையக்குத்துக் கோடுகளும் ஒரு புள்ளி வழிச்செல்லும் கோடுகளாக அமைவது வியப்பிற்குரியது !

செயல்பாடு

காகித மடிப்பு முறையில் முக்கோணத்தின் பக்கங்களின் மையக்குத்துக் கோடுகள் ஒரே புள்ளி வழிச் செல்வதை நாம் காண இயலும். முயற்சி செய்க! 

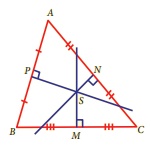
எந்தவொரு முக்கோணத்தின் பக்கங்களின் மையக்குத்துக்கோடுகளும் ஒருபுள்ளி வழிச் செல்லும் கோடுகளாகும். 

நடுக்கோட்டு மையம் காண்பதற்குச் செய்ததைப் போன்றே, குறுங்கோண, '' விரிகோண, செங்கோண, இருசமபக்க மற்றும் சமபக்க முக்கோணம் போன்ற வெவ்வேறு வகை முக்கோணங்களுக்கும் இச்செயல்பாட்டினை மீண்டும் செய்க. இவ்வகையில் சமபக்க முக்கோணங்களின் மையக்குத்துக் கோடுகள் ஏதேனும் சிறப்புத் தன்மையைப் பெற்றுள்ளனவா?

1. சுற்றுவட்ட மையம்

ஒரு முக்கோணத்தின் மூன்று பக்கங்களின் மையக்குத்துக் கோடுகளும் சந்திக்கும் புள்ளி அதன் சுற்றுவட்ட மையம் ஆகும். இது S என்ற எழுத்தால் குறிக்கப்படுகிறது. அது ஏன் அவ்வாறு அழைக்கப்படுகிறது? 

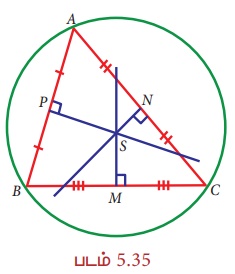
ஏனெனில், முக்கோணத்தின் பக்கங்களின் மையக்குத்துக்கோடுகள் சந்திக்கும் புள்ளியை சுற்றுவட்ட மையமாகக் கொண்டு, அம்முக்கோணத்தின் மூன்று உச்சிப்புள்ளிகள் வழியாகச் செல்லுமாறு முக்கோணத்தினைச் சுற்றிலும் ஒருவரால் வட்டத்தினை வரைய இயலும். இவ்வாறு, சுற்றுவட்ட மையமானது முக்கோணத்தின் உச்சிகளிலிருந்து சமதூரத்தில் அமைந்துள்ளது.

செயல்பாடு 

காகித மடிப்பு முறையில் பின்வருவனவற்றைச் சரியானவையா என ஆராய்க : 

1. குறுங்கோண முக்கோணத்தின் சுற்றுவட்டமையமானது அம்முக்கோணத்தின் உள்பகுதியிலேயே அமையும். 

2. விரிகோண முக்கோணத்தின் சுற்றுவட்டமையானது அம்முக்கோணத்தின் வெளிப்பகுதியிலேயே அமையும். 

3. செங்கோண முக்கோணத்தின் சுற்றுவட்டமையானது அம்முக்கோணத்தின் கர்ணத்தின் மையப்புள்ளியில் அமையும்.

எடுத்துக்காட்டு 5.19

∆ABC இல், S என்பது சுற்றுவட்ட மையம், BC = 72 செ.மீ மற்றும் DS = 15 செ.மீ எனில் சுற்றுவட்டத்தின் ஆரத்தைக் காண்க. 

தீர்வு:

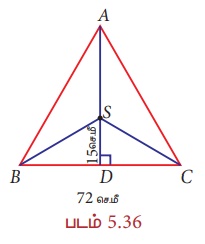
∆ABC இல் S என்பது சுற்றுவட்டமையமாகும் என்பதால், அது A, B மற்றும் C இலிருந்து சமதூரத்தில் இருக்கும். ஆகவே AS = BS = CS = சுற்றுவட்டத்தின் ஆரம். AD ஆனது BC இன் மையக்குத்துக்கோடு என்பதால், BD = × BC =  × 72 = 36 செ.மீ

செங்கோண முக்கோணம் BDS இல், பிதாகரஸ் தேற்றத்தின்படி, 

BS2 = BD2 + SD2 = 362 + 152 = 1521 = 392 ⇒ BS = 39 செ.மீ

∴  ∆ ABC இன் சுற்றுவட்டத்தின் ஆரம் = 39 செ.மீ ஆகும்.