பிதாகரஸ் தேற்றம்

பிதாகரஸ் தேற்றம்

கிரேக்க கணிதமேதை பிதாகரஸ் (கி.மு (பொ.ஆ.மு) 570−495) அவர்களின் பெயரில் உள்ள பிதாகரஸ் அல்லது பிதாகோரியன் தேற்றமானது, கணிதத்தில் உள்ள அனைத்துத் தேற்றங்களைக் காட்டிலும் மிகவும் முக்கியமான மற்றும் புகழ்வாய்ந்த தேற்றமாகும். வேறெந்தவொரு கணிதத்தேற்றத்தினைக் காட்டிலும், ஆயிரக்கணக்கான ஆண்டுகளாக தொடர்ந்து அதிகமான எண்ணிக்கையில் இதற்குப் பல்வேறு வடிவியல் மற்றும் இயற்கணித நிரூபணங்கள் வழங்கப்பட்டு வருகின்றன. 

தேற்றத்தின் கூற்று:

ஒரு செங்கோண முக்கோணத்தில் கர்ணத்தின் மீதமைந்த சதுரத்தின் பரப்பளவானது, மற்ற இரண்டு பக்கங்களின் மீதமைந்த சதுரங்களின் பரப்பளவுகளின் கூடுதலுக்குச் சமமாகும். அதாவது,

∆ ABC இல், BC2 = AB2 + AC2 ஆகும். 

காட்சி விளக்கம்:

கொடுக்கப்பட்டுள்ள படத்தில் 3 அலகுகள், 4 அலகுகள் மற்றும் 5 அலகுகள் பக்க அளவுகள் கொண்ட ஒரு முக்கோணம் உள்ளது. நன்கு அறியப்பட்ட இந்த 3 − 4 − 5 முக்கோணத்திலிருந்து பிதாகரஸ் தேற்றத்தினை, எளிமையாகக் காட்சிப்படுத்தவும் புரிந்து கொள்ளவும் முடியும்.

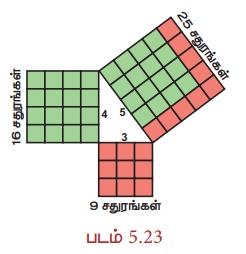
இப்படத்தில் 3 அலகுகள், 4 அலகுகள் ஆகிய அளவுகளைக் கொண்ட பக்கங்கள் செங்கோணத்தைத் தாங்கும் பக்கங்கள் ஆகும். 5 அலகுகள் கொண்ட பக்கமானது கர்ணம் என அழைக்கப்படுகிறது. கர்ணம் என்பது செங்கோண முக்கோணத்தின் மிகவும் நீளமான பக்கம் என்பதை நினைவில் கொள்க.

இப்போது, 5 அலகுகள் நீளமுள்ள கர்ணத்தின் மீதமைந்த சதுரத்தின் பரப்பளவு 5 × 5 = 25 சதுர அலகுகள் என்பதை நாம் எளிதில் காண இயலும். மேலும் 3 அலகுகள் மற்றும் 4 அலகுகள் நீளமுள்ள பக்கங்களின் மீதமைந்த சதுரங்கள் முறையே 3×3 = 9 சதுர அலகுகள் மற்றும் 4 × 4 = 16 சதுர அலகுகள் ஆகிய பரப்பளவுகளைப் பெற்றிருக்கும். எனவே தேற்றத்தின்படி, செங்கோண முக்கோணத்தின் கர்ணத்தின் மீதமைந்த சதுரத்தில் உள்ள ஓரலகு சதுரங்களின் எண்ணிக்கையானது, மற்ற இரண்டு பக்கங்களின் மீதமைந்த சதுரங்களில் உள்ள ஓரலகு சதுரங்களின் எண்ணிக்கைக்குச் சமமாக உள்ளன. வியப்பளிக்கிறதல்லவா?

ஆம். 5 × 5 = 3 × 3 + 4 × 4,

அதாவது 25 = 9 + 16 என்று சரியாக இருப்பதை நாம் காணலாம்.