முக்கோணத்தின் நடுக்கோடு

முக்கோணத்தின் நடுக்கோடு

ஒரு முக்கோணத்தின் உச்சிப் புள்ளியையும் அதன் எதிர்ப்பக்கத்தின் மையப் புள்ளியையும் இணைக்கும் கோடு அம்முக்கோணத்தின் நடுக்கோடு ஆகும்.

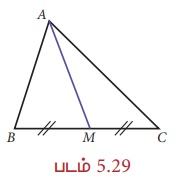
படத்தில், AM என்பது ∆ABC இன் நடுக்கோடாகும்.

∆ABC இக்கு வேறு ஏதேனும் நடுக்கோடுகள் உள்ளனவா? ஆம், ஒரு முக்கோணத்திற்கு மூன்று உச்சிப் புள்ளிகள் உள்ளதால் மூன்று நடுக்கோடுகளை ஒருவரால் காண இயலும்.

எடுத்துக்காட்டு 5.16

படத்தில் ABC என்பது ஒரு முக்கோணம் என்க AM என்பது அதன் நடுக்கோடுகளில் ஒன்றாகும். BM = 3.5 செ.மீ எனில் பக்கம் BC இன் நீளம் என்ன?

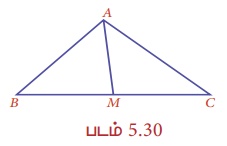
தீர்வு :

AM என்பது நடுக்கோடு ⇒ M ஆனது BC இன் நடுப்புள்ளி ஆகும். 

BM = 3.5 செ.மீ எனில், BC = BM இன் நீளத்தைப்போல் இருமடங்கு = 2 × 3.5 செ.மீ = 7 செ.மீ.

செயல்பாடு

1. முக்கோண வடிவ காகிதத்தை எடுத்துக் கொள்க (குறுங்கோண முக்கோணத்தைக் கொண்டு தொடங்குவோம்). அதற்கு ABC எனப் பெயரிடுக.

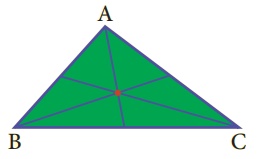
2. மடிப்புக் கோடானது உச்சிப்புள்ளி A வழியாகவும், B ஆனது C இன் மேல் பொருந்தும் நிலையில் BC ஐ சந்திக்குமாறும்  காகிதத்தினை மடிக்க

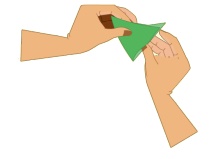
3. BC இன் மையப்புள்ளி M ஐக் குறிக்க.

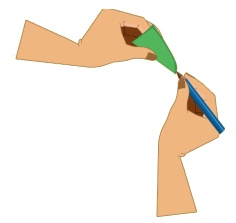
4. தெளிவாகக் காண விரும்பினால், இப்போது நீங்கள் நடுக்கோடு AM ஐ வரைந்து கொள்ளலாம் (அல்லது மடிப்பாகவே இருக்கலாம்)

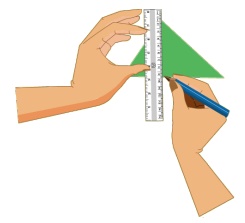
5. இதேபோன்று மடித்து, மற்ற இரண்டு நடுக்கோடுகளையும் வரைக. 

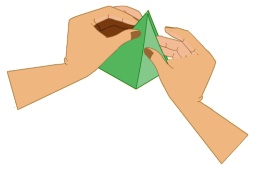
6. அனைத்து நடுக்கோடுகளும் ஒரேபுள்ளி  வழிச் செல்கின்றனவா? 

இப்போது இதே செயல்பாட்டினை மீண்டும் விரிகோண மற்றும் செங்கோண முக்கோணங்களுக்கும் செய்க. உங்களின் முடிவு என்ன? 

எந்தவொரு முக்கோணத்தின் மூன்று நடுக்கோடுகளும் ஒருபுள்ளி வழிச் செல்லும் கோடுகள் ஆகும்.

1. நடுக்கோட்டு மையம்

ஒரு முக்கோணத்தின் மூன்று நடுக்கோடுகள் சந்திக்கும் புள்ளி அதன் நடுக்கோட்டு மையம் ஆகும். இது G என்ற எழுத்தால் குறிக்கப்படுகிறது. இது புவிஈர்ப்பு மையமாகத் திகழ்வது ஒரு வியப்பாகும். இந்த உண்மையை ஒருவர் எளிதில் சரிபார்க்கலாம். முக்கோண வடிவில் உள்ள ஓர் அட்டையை எடுத்துக்கொள்க. அதன் நடுக்கோட்டு மையத்தினை விரல் நுனியிலோ அல்லது பென்சிலின் நுனியிலோ வைப்பதன் மூலம் அம்முக்கோணத்தைக் கிடைமட்டமாக நிலைநிறுத்த இயலும்.

முக்கோணத்தின் நடுக்கோட்டு மையத்தைக் காண மூன்று நடுக்கோடுகளையும் காண வேண்டுமா? இப்போது, பின்வரும் வினாக்களுக்கான விடைகளை நீங்களாகவே ஆராயலாம்.

(i) ஒரு முக்கோணத்தின் நடுக்கோட்டு மையத்தை எவ்வாறு காண்பீர்கள்? 

(ii) நடுக்கோட்டு மையமானது உச்சிப் புள்ளிகளிலிருந்து சமதூரத்தில் உள்ளனவா? 

(iii) ஒரு முக்கோணத்தின் நடுக்கோட்டு மையம் எப்போதும் அதன் உள்பகுதியிலேயே அமைகிறதா?

(iv) (அ) இருசமபக்க முக்கோணம் (ஆ) சமபக்க முக்கோணம் ஆகியவற்றின் நடுக்கோடுகளில் ஏதேனும் சிறப்புத்தன்மை உள்ளனவா? 

முக்கோணத்தின் நடுக்கோட்டு மையத்தின் பண்புகள்:

முக்கோணத்தின் நடுக்கோட்டு மையத்தின் அமைவிடமானது சில சிறப்புப் பண்புகளைக் கொண்டுள்ளது. 

•  எப்போதும் அது முக்கோணத்தின் உள்பகுதியிலேயே அமைகிறது. 

•  எந்தவொரு முக்கோணப்படலத்திற்கும் புவிஈர்ப்பு மையமாகத் திகழ்வதை நாம் ஏற்கனவே பார்த்திருக்கிறோம்.

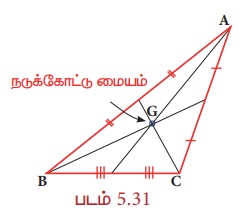
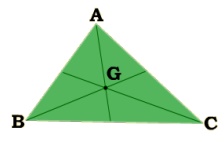
• கொடுக்கப்பட்டுள்ள படத்தை உற்றுநோக்குக. ஒவ்வோர் உச்சிப் புள்ளியிலிருந்தும் Gஇக்கு வரையப்பட்டுள்ள கோடுகள் ∆ABG, ∆BCG மற்றும் ∆CAG ஆகிய மூன்று முக்கோணங்களை உருவாக்குகிறது. வியக்கத்தக்க வகையில், இந்த மூன்று முக்கோணங்களும் சம பரப்பளவைக் கொண்டுள்ளன.

முக்கோணத்தின் நடுக்கோடுகள் அதனை சம பரப்பளவுள்ள மூன்று சிறிய முக்கோணங்களாகப் பிரிக்கும்!

உங்களுக்குத் தெரியுமா

முக்கோணத்தின் நடுக்கோட்டு மையமானது ஒவ்வொரு நடுக்கோட்டையும், உச்சிப் புள்ளிக்கு அருகாமையில் இருக்கும் கோட்டுத்துண்டு மற்றொன்றைப் போல் இருமடங்காக உள்ளவாறு இரண்டாகப் பிரிக்கிறது.

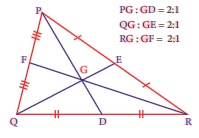
அதாவது, நடுக்கோட்டு மையமானது ஒவ்வொரு நடுக்கோட்டையும்  2:1 என்ற விகிதத்தில் பிரிக்கிறது (எடுத்துக்காட்டாக, GD ஆனது PD இல் பங்காகும்). (காகிதமடிப்பு முறையில் இதனைச் சரிபார்க்க முயற்சி செய்).

எடுத்துக்காட்டு 5.17

படத்தில், G ஆனது முக்கோணம் XYZ இன் நடுக்கோட்டு மையம் ஆகும். 

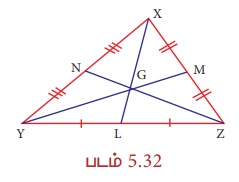
(i) GL = 2.5 செ.மீ எனில், XL இன் நீளம் காண்க.

(ii) YM = 9.3 செ.மீ எனில், GM இன் நீளம் காண்க. 

தீர்வு :

 (i) G ஆனது நடுக்கோட்டு மையம் என்பதால், XG : GL = 2:1

⇒ XG : 2.5 = 2 : 1.

எனவே, 1× (XG) = 2 × (2.5) ⇒ XG = 5 செ.மீ ஆகும்.

∴ XL இன் நீளம் = XG + GL = 5 + 2.5 = 7.5 செ.மீ. 

(ii) YG இன் நீளம் இரண்டு பங்கு எனில், GM இன் நீளம் 1 பங்கு ஆகும் (ஏன்?).

அதாவது YM இன் நீளம் 3 பங்குகள் ஆகும். 

3 பங்குகள் என்பது 9.3 செ.மீ நீளம் ஆகும். ஆகவே, GM இன் நீளம் (1பங்கு) = 9.3 ÷ 3 = 3.1 செ.மீ.

எடுத்துக்காட்டு 5.18

ABC ஆனது ஒரு முக்கோணம் மற்றும் G ஆனது அதன் நடுக்கோட்டு மையம் ஆகும். AD =12 செ.மீ, BC=8 செ.மீ மற்றும் BE = 9 செ.மீ எனில், ∆BDG இன் சுற்றளவைக் காண்க. 

தீர்வு:

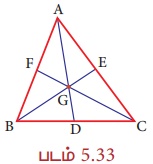
ABC ஆனது ஒரு முக்கோணம் மற்றும் G ஆனது அதன் நடுக்கோட்டு மையம் ஆகும்.

AD =12 செமீ ⇒ GD = AD இல் பங்கு = (12) = 4 செமீ மற்றும் 

BE = 9 செமீ  ⇒ BG= BE இல் பங்கு = (9) = 6 செ.மீ 

மேலும், D என்பது BC இன் மையப்புள்ளி ⇒ BD = BC இல் பங்கு = = 4 செ.மீ.

∴ ∆BDG இன் சுற்றளவு = BD + GD + BG = 4 + 4 + 6 = 14 செ.மீ