பிதாகரஸ் தேற்றத்தின் மறுதலை

பிதாகரஸ் தேற்றத்தின் மறுதலை

ஒருமுக்கோணத்தின் நீளமான பக்கத்தின் மீதமைந்த சதுரத்தின் பரப்பளவானது, மற்ற இரண்டு பக்கங்களின் மீதமைந்த சதுரங்களின் பரப்பளவுகளின் கூடுதலுக்குச் சமம் எனில், அந்த முக்கோணம் செங்கோண முக்கோணம் ஆகும்.

எடுத்துக்காட்டு: 

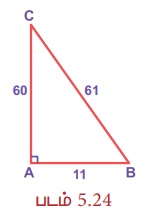
முக்கோணம் ABC இல், 

AB2 + AC2 = 112 + 602 = 3721 = 612 = BC2

எனவே, ∆ABC ஆனது ஒரு செங்கோண முக்கோணம் ஆகும்.

உங்களுக்குத் தெரியுமா?

i) பிதாகோரியன் தொடர்பை உண்மையாக்கும் வகையில் அமையும் சிறப்பு எண்கள் a, b மற்றும் c ஆனது பிதாகோரியன் மூன்றன் தொகுதி என அழைக்கப்படுகிறது.

எடுத்துக்காட்டு : (3,4,5) ஆனது ஒரு பிதாகோரியன் மூன்றன் தொகுதி ஆகும். 

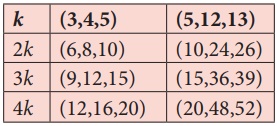
(ii) k என்பது 1 ஐ விட அதிகமான மிகை முழு மற்றும்  (a,b,c) ஆனது பிதாகரஸ் மூன்றன் தொகுதி எனில், (ka,kb,kc) என்பதும் பிதாகரஸ் மூன்றன் தொகுதியாக இருக்கும்.

எனவே, ஒரு பிதாகரஸ் மூன்றன் தொகுதியை 'k' ஆல் பெருக்க, எண்ணற்ற பிதாகரஸ் மூன்றன் தொகுதிகளை நாம் பெறலாம்.

இப்போது நாம் பிதாகரஸ் தேற்றத்தைப் பயன்படுத்தித் தீர்வு காணும் வகையில், சில எடுத்துக்காட்டுகளைக் காண்போம்.

எடுத்துக்காட்டு 5.11

படத்தில் AB ⊥ AC எனில், 

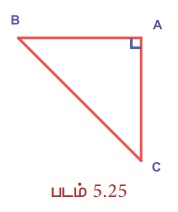
1) ∆ABC இன் வகை என்ன? 

2) ∆ABC இல், AB மற்றும் AC என்பன எவற்றைக் குறிக்கின்றன? 

3) CB ஐ எவ்வாறு அழைப்பாய்? 

4) AC = AB எனில், ∠B மற்றும் ∠C ஆகியவற்றின் அளவுகள் என்ன?

தீர்வு:

a) A இல் AB ⊥ AC ஆக இருப்பதால், ∆ABC ஆனது ஒரு செங்கோண முக்கோணமாகும்.

b) ∆ABC இல், AB மற்றும் AC ஆகியவை செங்கோணத்தைத் தாங்கும் பக்கங்கள் ஆகும். 

c) CB என்பது கர்ணம் ஆகும்.

 d) ∠B + ∠C = 90° மற்றும் சமபக்கங்களுக்கு எதிரேயுள்ள கோணங்கள் சமம். எனவே, ∠B = ∠C = 90° / 2  = 45°

எடுத்துக்காட்டு 5.12 

ஒரு செங்கோண முக்கோணமானது 5 செ.மீ, 12 செ.மீ மற்றும் 13 செ.மீ ஆகிய அளவுகளைக் கொண்ட பக்கங்களைப் பெற்றிருக்க இயலுமா? 

தீர்வு: 

a = 5 , b = 12 மற்றும் c = 13 எனக் கொள்க. 

இப்போது, a2 + b2 = 52 + 122 = 25 + 144 = 169 = 132 = c2

பிதாகரஸ் தேற்றத்தின் மறுதலையின்படி, கொடுக்கப்பட்ட பக்க அளவுகளைக் கொண்ட முக்கோணம் ஒரு செங்கோண முக்கோணம் ஆகும்.

எடுத்துக்காட்டு 5.13

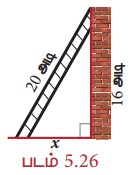
20 அடி நீளமுள்ள ஏணி, தரையிலிருந்து 16 அடி உயரத்தில் சுவரினைத்  தொடுமாறு சாய்த்து வைக்கப்பட்டுள்ளது எனில், சுவரிலிருந்து ஏணியின் அடிப்பகுதியானது எவ்வளவு தூரத்தில் உள்ளது?

தீர்வு:

ஏணி, சுவர் மற்றும் தரை ஆகியவை ஏணியைக் கர்ணமாகக் கொண்ட ஒரு செங்கோண முக்கோணத்தை உருவாக்குகிறது. படத்திலிருந்து பிதாகரஸ் தேற்றத்தின்படி,

202 = 162 + x2   ⇒ 400 = 256 + x2   ⇒ x2 = 400 – 256 =144 =122   ⇒       x = 12 அடி 

எனவே, ஏணியின் அடிப்பகுதியானது சுவரிலிருந்து 12 அடி தூரத்தில் உள்ளது.

எடுத்துக்காட்டு 5.14 

படத்திலிருந்து LM, MN, LN ஆகியவற்றையும், ∆LON இன் பரப்பளவையும் காண்க. 

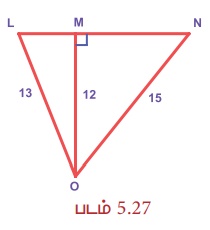
தீர்வு: 

∆LMO இலிருந்து, பிதாகரஸ் தேற்றத்தின்படி,

LM2 = OL2 – OM2 

⇒ LM2 = 132 − 122 = 169−144 = 25 = 52

∴ LM = 5 அலகுகள்

 ∆NMO இலிருந்து, பிதாகரஸ் தேற்றத்தின்படி,

MN2 = ON2 – OM2 

=152 − 122 = 225 −144 = 81 = 92

∴ MN = 9 அலகுகள்

எனவே, LN = LM + MN = 5+9 = 14 அலகுகள்

∆LON இன் பரப்பளவு =  × அடிப்பக்கம் × உயரம்

= × LN × OM =  × 14 × 12 

= 84 சதுர அலகுகள்.

செயல்பாடு

1. பிதாகரஸ் மூன்றன் தொகுதியைப் பின்வருமாறு நாம் உருவாக்கலாம். 

m மற்றும் n ஆகியவை ஏதேனும் இரண்டு மிகை முழுக்கள் என்க (m > n). 

a = m2 − n2 , b = 2mn மற்றும் c = m2 + n2 எனில், (a, b, c) ஆனது ஒரு பிதாகரஸ் மூன்றன் தொகுதியாகும். (ஏன்? எனச் சிந்திக்க) 

அட்டவணையை நிரப்புக. 

 2. கர்ணம் 85 ஆகவும் மற்ற இரு பக்க அளவுகள் முழுக்களாகவும் உடைய செங்கோண முக்கோணத்தின் பக்க அளவுகளைக் காண்க.

எடுத்துக்காட்டு 5.15 

∆ABC என்பது ஒரு சமபக்க முக்கோணம் மற்றும் செங்கோண முக்கோணம் BCD இல் CD ஆனது 8 செ.மீ எனில், சமபக்க ∆ABC இன் பக்கம் மற்றும் BD ஐக் காண்க. 

தீர்வு : 

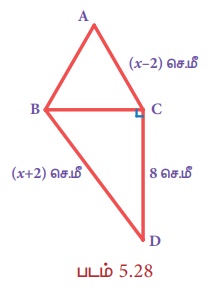
∆ABC ஒரு சமபக்க முக்கோணம் என்பதால்,

படத்திலிருந்து, AB = BC = AC = (x−2) செ.மீ 

∴ ∆BCD இலிருந்து, பிதாகரஸ் தேற்றத்தின்படி,

BD2 = BC2 + CD2 ⇒ (x+2)2 = (x − 2)2 + 82 

x2 + 4x + 4 = x2 – 4x + 4 + 82 ⇒ 8x = 82 ⇒ x = 8 செ.மீ 

∴ சமபக்க ∆ABC இன் பக்கம் = 6 செ.மீ மற்றும் BD = 10 செ.மீ.